Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 14758 by Tinkutara last updated on 04/Jun/17

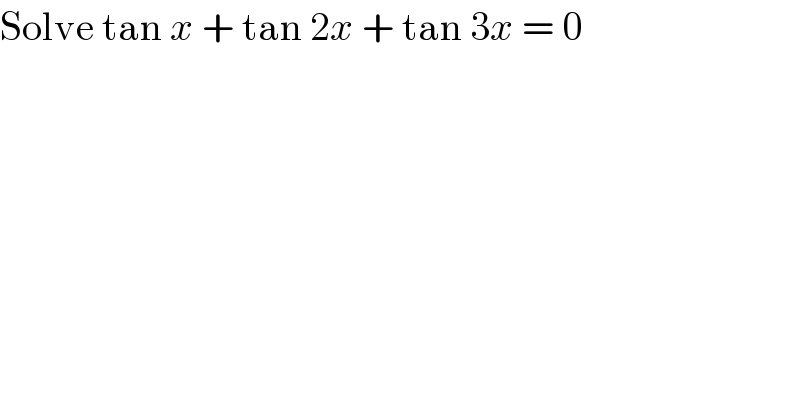
Solve tan x + tan 2x + tan 3x = 0

$$\mathrm{Solve}\:\mathrm{tan}\:{x}\:+\:\mathrm{tan}\:\mathrm{2}{x}\:+\:\mathrm{tan}\:\mathrm{3}{x}\:=\:\mathrm{0} \\ $$

Commented by Tinkutara last updated on 04/Jun/17

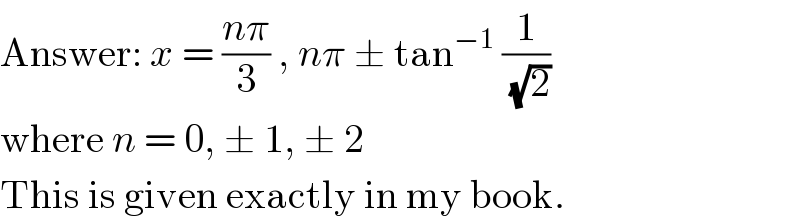
Answer: x = ((nπ)/3) , nπ ± tan^(−1) (1/(√2)) where n = 0, ± 1, ± 2 This is given exactly in my book.

$$\mathrm{Answer}:\:{x}\:=\:\frac{{n}\pi}{\mathrm{3}}\:,\:{n}\pi\:\pm\:\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\mathrm{where}\:{n}\:=\:\mathrm{0},\:\pm\:\mathrm{1},\:\pm\:\mathrm{2} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{given}\:\mathrm{exactly}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book}. \\ $$

Commented by ajfour last updated on 04/Jun/17

what about x=nπ.

$${what}\:{about}\:{x}={n}\pi. \\ $$

Commented by Tinkutara last updated on 04/Jun/17

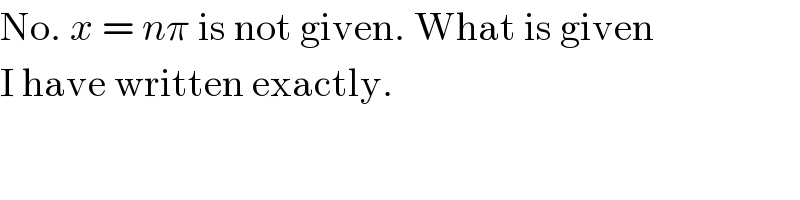
No. x = nπ is not given. What is given I have written exactly.

$$\mathrm{No}.\:{x}\:=\:{n}\pi\:\mathrm{is}\:\mathrm{not}\:\mathrm{given}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{given} \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{written}\:\mathrm{exactly}. \\ $$

Commented by mrW1 last updated on 04/Jun/17

x=nπ is definitively a solution. This can be easily checked.

$${x}={n}\pi\:{is}\:{definitively}\:{a}\:{solution}.\:{This} \\ $$$${can}\:{be}\:{easily}\:{checked}. \\ $$

Answered by mrW1 last updated on 04/Jun/17

tan x+tan 2x=−tan 3x=−tan (x+2x) tan x+tan 2x=−((tan x+tan 2x)/(1−tan x tan 2x)) ⇒tan x+tan 2x=0 ...(1) or 1−tan x tan 2x=−1 ⇒tan x tan 2x=2 ...(2) (1) tan x=−tan 2x=−((2tan x)/(1−tan^2 x)) ⇒tan x=0 ...(1.1) or 1−tan^2 x=−2 ⇒tan^2 x=3 ⇒tan x=±(√3) ...(1.2) (2) tan x ((2tan x)/(1−tan^2 x))=2 ((tan^2 x)/(1−tan^2 x))=1 tan^2 x=(1/2) ⇒tan x=±(1/(√2)) ...(2) All solutions with k∈Z: (1.1)⇒ x=kπ (1.2)⇒ x=kπ±tan^(−1) (√3)=kπ±(π/3) (2)⇒ x=kπ±tan^(−1) (1/(√2))= or =kπ+(π/2)±tan^(−1) (√2)

$$\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}=−\mathrm{tan}\:\mathrm{3}{x}=−\mathrm{tan}\:\left({x}+\mathrm{2}{x}\right) \\ $$$$\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}=−\frac{\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{1}−\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}} \\ $$$$\Rightarrow\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}=\mathrm{0}\:\:...\left(\mathrm{1}\right) \\ $$$${or} \\ $$$$\mathrm{1}−\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}=\mathrm{2}\:\:\:\:...\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right) \\ $$$$\mathrm{tan}\:{x}=−\mathrm{tan}\:\mathrm{2}{x}=−\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}} \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\mathrm{0}\:\:\:\:\:\:...\left(\mathrm{1}.\mathrm{1}\right) \\ $$$${or} \\ $$$$\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}=−\mathrm{2} \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \:{x}=\mathrm{3}\:\:\:\:\: \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\pm\sqrt{\mathrm{3}}\:\:\:\:...\left(\mathrm{1}.\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{tan}\:{x}\:\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}}=\mathrm{2} \\ $$$$\frac{\mathrm{tan}^{\mathrm{2}} \:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}}=\mathrm{1} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\:\:\:...\left(\mathrm{2}\right) \\ $$$$ \\ $$$${All}\:{solutions}\:{with}\:{k}\in\mathbb{Z}: \\ $$$$\left(\mathrm{1}.\mathrm{1}\right)\Rightarrow\:{x}={k}\pi \\ $$$$\left(\mathrm{1}.\mathrm{2}\right)\Rightarrow\:{x}={k}\pi\pm\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{3}}={k}\pi\pm\frac{\pi}{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\Rightarrow\:{x}={k}\pi\pm\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{2}}}=\:{or}\:={k}\pi+\frac{\pi}{\mathrm{2}}\pm\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{2}} \\ $$

Commented by Tinkutara last updated on 04/Jun/17

But answer given in my book is different!

$$\mathrm{But}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book}\:\mathrm{is} \\ $$$$\mathrm{different}! \\ $$

Commented by mrW1 last updated on 04/Jun/17

I had a mistake. It′s corrected now.

$${I}\:{had}\:{a}\:{mistake}.\:{It}'{s}\:{corrected}\:{now}. \\ $$

Answered by ajfour last updated on 04/Jun/17

let tan x=t t+((2t)/(1−t^2 ))+((t(3−t^2 ))/(1−3t^2 ))=0 ⇒ t^2 ≠1, 3 now, factorising to get, t[1+(2/(1−t^2 ))+((3−t^2 )/(1−3t^2 ))]=0 t[((3−t^2 )/(1−t^2 ))+((3−t^2 )/(1−3t^2 ))]=0 t(3−t^2 )[((2−4t^2 )/((1−t^2 )(1−3t^2 )))]=0 ⇒ t=tan x=0 , ±(√3) , ±(1/(√2)) x=n𝛑, n𝛑±(𝛑/3), n𝛑±tan^(−1) (1/(√2)) .

$${let}\:\mathrm{tan}\:{x}={t} \\ $$$$\:{t}+\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}^{\mathrm{2}} \neq\mathrm{1},\:\mathrm{3} \\ $$$$\:{now},\:{factorising}\:{to}\:{get}, \\ $$$$\:\:\:\:\:\:{t}\left[\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{3}−{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{t}\left[\frac{\mathrm{3}−{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{3}−{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$$\:\:\:{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)\left[\frac{\mathrm{2}−\mathrm{4}{t}^{\mathrm{2}} }{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} \right)}\right]=\mathrm{0} \\ $$$$\:\:\Rightarrow\:\:{t}=\mathrm{tan}\:{x}=\mathrm{0}\:,\:\pm\sqrt{\mathrm{3}}\:,\:\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\: \\ $$$$\boldsymbol{{x}}=\boldsymbol{{n}\pi},\:\boldsymbol{{n}\pi}\pm\frac{\boldsymbol{\pi}}{\mathrm{3}},\:\boldsymbol{{n}\pi}\pm\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:. \\ $$

Commented by Tinkutara last updated on 04/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com