
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 147688 by mathmax by abdo last updated on 22/Jul/21
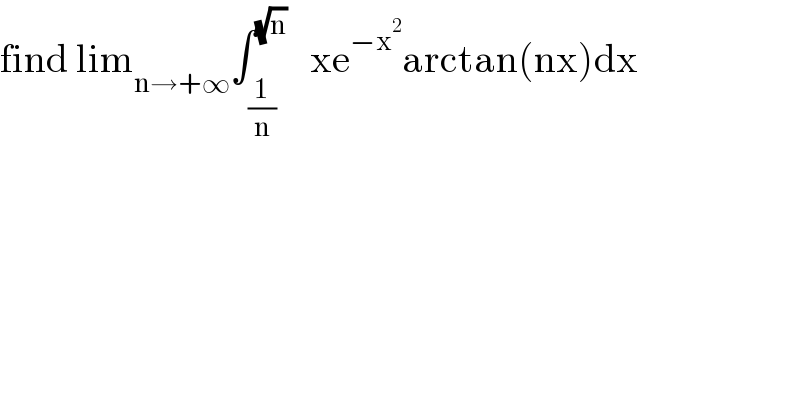
Answered by ArielVyny last updated on 24/Jul/21
![according that lim ∫f(x)dx=∫limf(x)dx we have lim_(n→+∞) ∫_(1/n) ^(√n) xe^(−x^2 ) arctan(nx)dx =(π/2)∫_0 ^(+∞) xe^(−x^2 ) dx x^2 =t→2xdx=dt ∫_0 ^(+∞) e^(−t) (1/2)dt=(1/2)[−e^(−t) ]_0 ^(+∞) =(1/2)[0+1]=(1/2) lim_(n→+∞) ∫_(1/n) ^(√n) xe^(−x^2 ) arctg(nx)dx=(π/4)](Q147874.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 147688 by mathmax by abdo last updated on 22/Jul/21 | ||
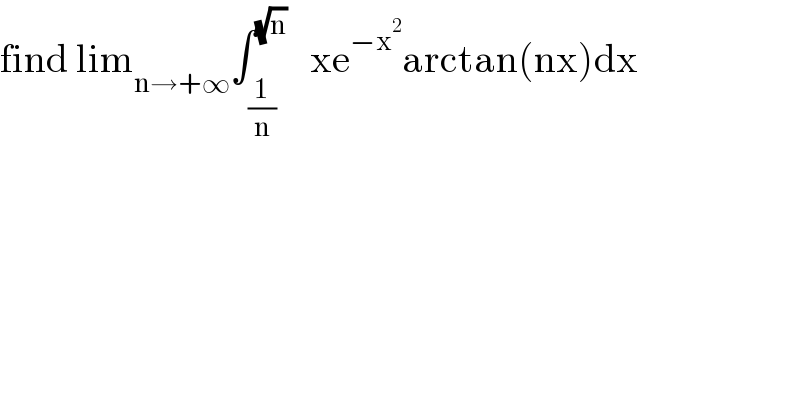 | ||
Answered by ArielVyny last updated on 24/Jul/21 | ||
![according that lim ∫f(x)dx=∫limf(x)dx we have lim_(n→+∞) ∫_(1/n) ^(√n) xe^(−x^2 ) arctan(nx)dx =(π/2)∫_0 ^(+∞) xe^(−x^2 ) dx x^2 =t→2xdx=dt ∫_0 ^(+∞) e^(−t) (1/2)dt=(1/2)[−e^(−t) ]_0 ^(+∞) =(1/2)[0+1]=(1/2) lim_(n→+∞) ∫_(1/n) ^(√n) xe^(−x^2 ) arctg(nx)dx=(π/4)](Q147874.png) | ||
| ||