Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 147791 by Tawa11 last updated on 23/Jul/21

If a + b + c + d = 1 a^2 + b^2 + c^2 + d^2 = 2 a^3 + b^3 + c^3 + d^3 = 3 a^4 + b^4 + c^4 + d^4 = 4 Evaluate: a^6 + b^6 + c^6 + d^6

$$\mathrm{If}\:\:\:\:\:\:\:\mathrm{a}\:\:+\:\:\mathrm{b}\:\:+\:\:\mathrm{c}\:\:+\:\:\mathrm{d}\:\:\:=\:\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} \:\:+\:\:\mathrm{b}^{\mathrm{2}} \:\:+\:\:\mathrm{c}^{\mathrm{2}} \:\:+\:\:\mathrm{d}^{\mathrm{2}} \:\:=\:\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{3}} \:\:+\:\:\mathrm{b}^{\mathrm{3}} \:\:+\:\:\mathrm{c}^{\mathrm{3}} \:\:+\:\:\mathrm{d}^{\mathrm{3}} \:\:=\:\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{4}} \:\:+\:\:\mathrm{b}^{\mathrm{4}} \:\:+\:\:\mathrm{c}^{\mathrm{4}} \:\:+\:\:\mathrm{d}^{\mathrm{4}} \:\:=\:\:\mathrm{4} \\ $$$$\mathrm{Evaluate}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{6}} \:\:+\:\:\mathrm{b}^{\mathrm{6}} \:\:+\:\:\mathrm{c}^{\mathrm{6}} \:\:+\:\:\mathrm{d}^{\mathrm{6}} \\ $$

Commented by prakash jain last updated on 25/Jul/21

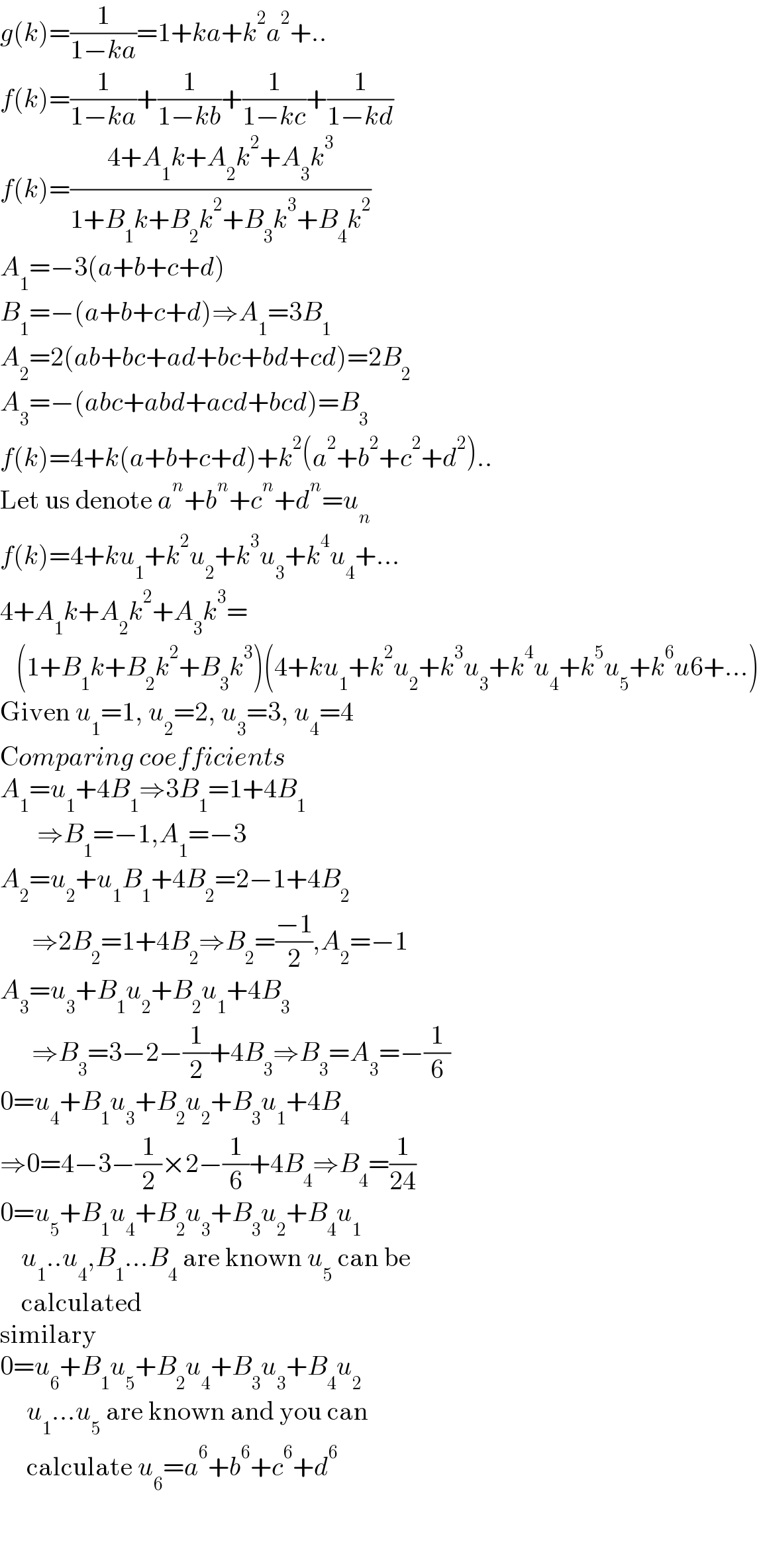
g(k)=(1/(1−ka))=1+ka+k^2 a^2 +.. f(k)=(1/(1−ka))+(1/(1−kb))+(1/(1−kc))+(1/(1−kd)) f(k)=((4+A_1 k+A_2 k^2 +A_3 k^3 )/(1+B_1 k+B_2 k^2 +B_3 k^3 +B_4 k^2 )) A_1 =−3(a+b+c+d) B_1 =−(a+b+c+d)⇒A_1 =3B_1 A_2 =2(ab+bc+ad+bc+bd+cd)=2B_2 A_3 =−(abc+abd+acd+bcd)=B_3 f(k)=4+k(a+b+c+d)+k^2 (a^2 +b^2 +c^2 +d^2 ).. Let us denote a^n +b^n +c^n +d^n =u_n f(k)=4+ku_1 +k^2 u_2 +k^3 u_3 +k^4 u_4 +... 4+A_1 k+A_2 k^2 +A_3 k^3 = (1+B_1 k+B_2 k^2 +B_3 k^3 )(4+ku_1 +k^2 u_2 +k^3 u_3 +k^4 u_4 +k^5 u_5 +k^6 u6+...) Given u_1 =1, u_2 =2, u_3 =3, u_4 =4 Comparing coefficients A_1 =u_1 +4B_1 ⇒3B_1 =1+4B_1 ⇒B_1 =−1,A_1 =−3 A_2 =u_2 +u_1 B_1 +4B_2 =2−1+4B_2 ⇒2B_2 =1+4B_2 ⇒B_2 =((−1)/2),A_2 =−1 A_3 =u_3 +B_1 u_2 +B_2 u_1 +4B_3 ⇒B_3 =3−2−(1/2)+4B_3 ⇒B_3 =A_3 =−(1/6) 0=u_4 +B_1 u_3 +B_2 u_2 +B_3 u_1 +4B_4 ⇒0=4−3−(1/2)×2−(1/6)+4B_4 ⇒B_4 =(1/(24)) 0=u_5 +B_1 u_4 +B_2 u_3 +B_3 u_2 +B_4 u_1 u_1 ..u_4 ,B_1 ...B_4 are known u_5 can be calculated similary 0=u_6 +B_1 u_5 +B_2 u_4 +B_3 u_3 +B_4 u_2 u_1 ...u_5 are known and you can calculate u_6 =a^6 +b^6 +c^6 +d^6

$${g}\left({k}\right)=\frac{\mathrm{1}}{\mathrm{1}−{ka}}=\mathrm{1}+{ka}+{k}^{\mathrm{2}} {a}^{\mathrm{2}} +.. \\ $$$${f}\left({k}\right)=\frac{\mathrm{1}}{\mathrm{1}−{ka}}+\frac{\mathrm{1}}{\mathrm{1}−{kb}}+\frac{\mathrm{1}}{\mathrm{1}−{kc}}+\frac{\mathrm{1}}{\mathrm{1}−{kd}} \\ $$$${f}\left({k}\right)=\frac{\mathrm{4}+{A}_{\mathrm{1}} {k}+{A}_{\mathrm{2}} {k}^{\mathrm{2}} +{A}_{\mathrm{3}} {k}^{\mathrm{3}} }{\mathrm{1}+{B}_{\mathrm{1}} {k}+{B}_{\mathrm{2}} {k}^{\mathrm{2}} +{B}_{\mathrm{3}} {k}^{\mathrm{3}} +{B}_{\mathrm{4}} {k}^{\mathrm{2}} } \\ $$$${A}_{\mathrm{1}} =−\mathrm{3}\left({a}+{b}+{c}+{d}\right) \\ $$$${B}_{\mathrm{1}} =−\left({a}+{b}+{c}+{d}\right)\Rightarrow{A}_{\mathrm{1}} =\mathrm{3}{B}_{\mathrm{1}} \\ $$$${A}_{\mathrm{2}} =\mathrm{2}\left({ab}+{bc}+{ad}+{bc}+{bd}+{cd}\right)=\mathrm{2}{B}_{\mathrm{2}} \\ $$$${A}_{\mathrm{3}} =−\left({abc}+{abd}+{acd}+{bcd}\right)={B}_{\mathrm{3}} \\ $$$${f}\left({k}\right)=\mathrm{4}+{k}\left({a}+{b}+{c}+{d}\right)+{k}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right).. \\ $$$$\mathrm{Let}\:\mathrm{us}\:\mathrm{denote}\:{a}^{{n}} +{b}^{{n}} +{c}^{{n}} +{d}^{{n}} ={u}_{{n}} \\ $$$${f}\left({k}\right)=\mathrm{4}+{ku}_{\mathrm{1}} +{k}^{\mathrm{2}} {u}_{\mathrm{2}} +{k}^{\mathrm{3}} {u}_{\mathrm{3}} +{k}^{\mathrm{4}} {u}_{\mathrm{4}} +... \\ $$$$\mathrm{4}+{A}_{\mathrm{1}} {k}+{A}_{\mathrm{2}} {k}^{\mathrm{2}} +{A}_{\mathrm{3}} {k}^{\mathrm{3}} = \\ $$$$\:\:\:\left(\mathrm{1}+{B}_{\mathrm{1}} {k}+{B}_{\mathrm{2}} {k}^{\mathrm{2}} +{B}_{\mathrm{3}} {k}^{\mathrm{3}} \right)\left(\mathrm{4}+{ku}_{\mathrm{1}} +{k}^{\mathrm{2}} {u}_{\mathrm{2}} +{k}^{\mathrm{3}} {u}_{\mathrm{3}} +{k}^{\mathrm{4}} {u}_{\mathrm{4}} +{k}^{\mathrm{5}} {u}_{\mathrm{5}} +{k}^{\mathrm{6}} {u}\mathrm{6}+...\right) \\ $$$$\mathrm{Given}\:{u}_{\mathrm{1}} =\mathrm{1},\:{u}_{\mathrm{2}} =\mathrm{2},\:{u}_{\mathrm{3}} =\mathrm{3},\:{u}_{\mathrm{4}} =\mathrm{4} \\ $$$$\mathrm{C}{omparing}\:{coefficients} \\ $$$${A}_{\mathrm{1}} ={u}_{\mathrm{1}} +\mathrm{4}{B}_{\mathrm{1}} \Rightarrow\mathrm{3}{B}_{\mathrm{1}} =\mathrm{1}+\mathrm{4}{B}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\Rightarrow{B}_{\mathrm{1}} =−\mathrm{1},{A}_{\mathrm{1}} =−\mathrm{3} \\ $$$${A}_{\mathrm{2}} ={u}_{\mathrm{2}} +{u}_{\mathrm{1}} {B}_{\mathrm{1}} +\mathrm{4}{B}_{\mathrm{2}} =\mathrm{2}−\mathrm{1}+\mathrm{4}{B}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\Rightarrow\mathrm{2}{B}_{\mathrm{2}} =\mathrm{1}+\mathrm{4}{B}_{\mathrm{2}} \Rightarrow{B}_{\mathrm{2}} =\frac{−\mathrm{1}}{\mathrm{2}},{A}_{\mathrm{2}} =−\mathrm{1} \\ $$$${A}_{\mathrm{3}} ={u}_{\mathrm{3}} +{B}_{\mathrm{1}} {u}_{\mathrm{2}} +{B}_{\mathrm{2}} {u}_{\mathrm{1}} +\mathrm{4}{B}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\Rightarrow{B}_{\mathrm{3}} =\mathrm{3}−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{4}{B}_{\mathrm{3}} \Rightarrow{B}_{\mathrm{3}} ={A}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{0}={u}_{\mathrm{4}} +{B}_{\mathrm{1}} {u}_{\mathrm{3}} +{B}_{\mathrm{2}} {u}_{\mathrm{2}} +{B}_{\mathrm{3}} {u}_{\mathrm{1}} +\mathrm{4}{B}_{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{0}=\mathrm{4}−\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}−\frac{\mathrm{1}}{\mathrm{6}}+\mathrm{4}{B}_{\mathrm{4}} \Rightarrow{B}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{24}} \\ $$$$\mathrm{0}={u}_{\mathrm{5}} +{B}_{\mathrm{1}} {u}_{\mathrm{4}} +{B}_{\mathrm{2}} {u}_{\mathrm{3}} +{B}_{\mathrm{3}} {u}_{\mathrm{2}} +{B}_{\mathrm{4}} {u}_{\mathrm{1}} \\ $$$$\:\:\:\:{u}_{\mathrm{1}} ..{u}_{\mathrm{4}} ,{B}_{\mathrm{1}} ...{B}_{\mathrm{4}} \:\mathrm{are}\:\mathrm{known}\:{u}_{\mathrm{5}} \:\mathrm{can}\:\mathrm{be} \\ $$$$\:\:\:\:\mathrm{calculated} \\ $$$$\mathrm{similary} \\ $$$$\mathrm{0}={u}_{\mathrm{6}} +{B}_{\mathrm{1}} {u}_{\mathrm{5}} +{B}_{\mathrm{2}} {u}_{\mathrm{4}} +{B}_{\mathrm{3}} {u}_{\mathrm{3}} +{B}_{\mathrm{4}} {u}_{\mathrm{2}} \\ $$$$\:\:\:\:\:{u}_{\mathrm{1}} ...{u}_{\mathrm{5}} \:\mathrm{are}\:\mathrm{known}\:\mathrm{and}\:\mathrm{you}\:\mathrm{can} \\ $$$$\:\:\:\:\:\mathrm{calculate}\:{u}_{\mathrm{6}} ={a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} +{d}^{\mathrm{6}} \\ $$$$ \\ $$

Commented by prakash jain last updated on 25/Jul/21

u_5 −4−(3/2)−(1/3)+(1/(24))=0 u_5 =((96+36+8−1)/(24))=((139)/(24)) u_6 −((139)/(24))−(1/2)×4−(1/6)×3+(1/(24))×2 u_6 =((139)/(24))+2+(1/2)−(1/(12))=((139+48+12−2)/(24)) =((197)/(24)) a^6 +b^6 +c^6 +d^6 =((197)/(24)) I haven′t checked numerical calculation thoroughly so please recheck these. You can use this method to find any u_n =a^n +b^n +c^n +d^n

$${u}_{\mathrm{5}} −\mathrm{4}−\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{24}}=\mathrm{0} \\ $$$${u}_{\mathrm{5}} =\frac{\mathrm{96}+\mathrm{36}+\mathrm{8}−\mathrm{1}}{\mathrm{24}}=\frac{\mathrm{139}}{\mathrm{24}} \\ $$$${u}_{\mathrm{6}} −\frac{\mathrm{139}}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}−\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{3}+\frac{\mathrm{1}}{\mathrm{24}}×\mathrm{2} \\ $$$${u}_{\mathrm{6}} =\frac{\mathrm{139}}{\mathrm{24}}+\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{12}}=\frac{\mathrm{139}+\mathrm{48}+\mathrm{12}−\mathrm{2}}{\mathrm{24}} \\ $$$$=\frac{\mathrm{197}}{\mathrm{24}} \\ $$$${a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} +{d}^{\mathrm{6}} =\frac{\mathrm{197}}{\mathrm{24}} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{checked}\:\mathrm{numerical}\:\mathrm{calculation} \\ $$$$\mathrm{thoroughly}\:\mathrm{so}\:\mathrm{please}\:\mathrm{recheck}\:\mathrm{these}. \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{use}\:\mathrm{this}\:\mathrm{method}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{any}\:{u}_{{n}} ={a}^{{n}} +{b}^{{n}} +{c}^{{n}} +{d}^{{n}} \\ $$

Commented by Tawa11 last updated on 25/Jul/21

Thanks sir. I appreciate. God bless you.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Answered by Rasheed.Sindhi last updated on 23/Jul/21

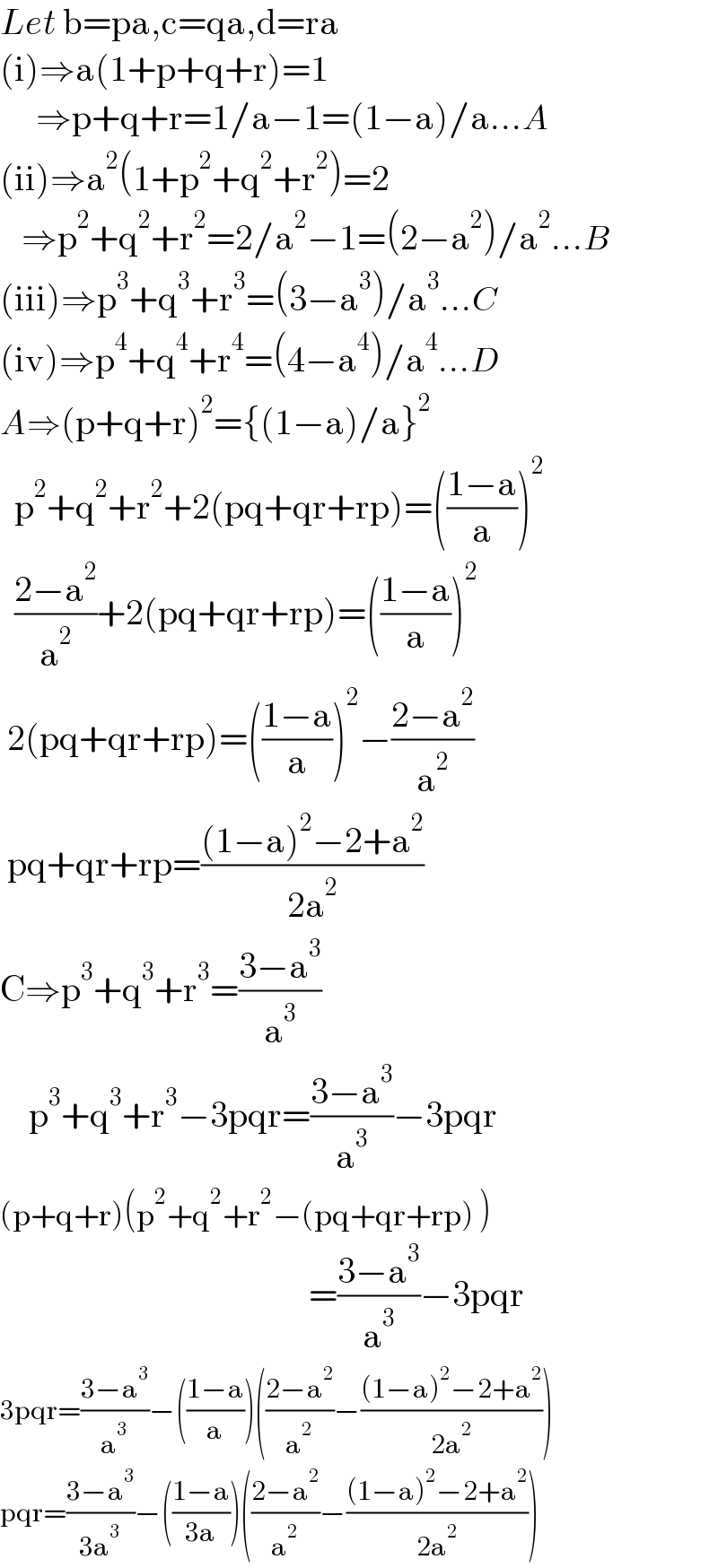
Let b=pa,c=qa,d=ra (i)⇒a(1+p+q+r)=1 ⇒p+q+r=1/a−1=(1−a)/a...A (ii)⇒a^2 (1+p^2 +q^2 +r^2 )=2 ⇒p^2 +q^2 +r^2 =2/a^2 −1=(2−a^2 )/a^2 ...B (iii)⇒p^3 +q^3 +r^3 =(3−a^3 )/a^3 ...C (iv)⇒p^4 +q^4 +r^4 =(4−a^4 )/a^4 ...D A⇒(p+q+r)^2 ={(1−a)/a}^2 p^2 +q^2 +r^2 +2(pq+qr+rp)=(((1−a)/a))^2 ((2−a^2 )/a^2 )+2(pq+qr+rp)=(((1−a)/a))^2 2(pq+qr+rp)=(((1−a)/a))^2 −((2−a^2 )/a^2 ) pq+qr+rp=(((1−a)^2 −2+a^2 )/(2a^2 )) C⇒p^3 +q^3 +r^3 =((3−a^3 )/a^3 ) p^3 +q^3 +r^3 −3pqr=((3−a^3 )/a^3 )−3pqr (p+q+r)(p^2 +q^2 +r^2 −(pq+qr+rp) ) =((3−a^3 )/a^3 )−3pqr 3pqr=((3−a^3 )/a^3 )−(((1−a)/a))(((2−a^2 )/a^2 )−(((1−a)^2 −2+a^2 )/(2a^2 ))) pqr=((3−a^3 )/(3a^3 ))−(((1−a)/(3a)))(((2−a^2 )/a^2 )−(((1−a)^2 −2+a^2 )/(2a^2 )))

$${Let}\:\mathrm{b}=\mathrm{pa},\mathrm{c}=\mathrm{qa},\mathrm{d}=\mathrm{ra} \\ $$$$\left(\mathrm{i}\right)\Rightarrow\mathrm{a}\left(\mathrm{1}+\mathrm{p}+\mathrm{q}+\mathrm{r}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{p}+\mathrm{q}+\mathrm{r}=\mathrm{1}/\mathrm{a}−\mathrm{1}=\left(\mathrm{1}−\mathrm{a}\right)/\mathrm{a}...{A} \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \right)=\mathrm{2} \\ $$$$\:\:\:\Rightarrow\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\mathrm{2}/\mathrm{a}^{\mathrm{2}} −\mathrm{1}=\left(\mathrm{2}−\mathrm{a}^{\mathrm{2}} \right)/\mathrm{a}^{\mathrm{2}} ...{B} \\ $$$$\left(\mathrm{iii}\right)\Rightarrow\mathrm{p}^{\mathrm{3}} +\mathrm{q}^{\mathrm{3}} +\mathrm{r}^{\mathrm{3}} =\left(\mathrm{3}−\mathrm{a}^{\mathrm{3}} \right)/\mathrm{a}^{\mathrm{3}} ...{C} \\ $$$$\left(\mathrm{iv}\right)\Rightarrow\mathrm{p}^{\mathrm{4}} +\mathrm{q}^{\mathrm{4}} +\mathrm{r}^{\mathrm{4}} =\left(\mathrm{4}−\mathrm{a}^{\mathrm{4}} \right)/\mathrm{a}^{\mathrm{4}} ...{D} \\ $$$${A}\Rightarrow\left(\mathrm{p}+\mathrm{q}+\mathrm{r}\right)^{\mathrm{2}} =\left\{\left(\mathrm{1}−\mathrm{a}\right)/\mathrm{a}\right\}^{\mathrm{2}} \\ $$$$\:\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{pq}+\mathrm{qr}+\mathrm{rp}\right)=\left(\frac{\mathrm{1}−\mathrm{a}}{\mathrm{a}}\right)^{\mathrm{2}} \\ $$$$\:\:\frac{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\mathrm{2}\left(\mathrm{pq}+\mathrm{qr}+\mathrm{rp}\right)=\left(\frac{\mathrm{1}−\mathrm{a}}{\mathrm{a}}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{2}\left(\mathrm{pq}+\mathrm{qr}+\mathrm{rp}\right)=\left(\frac{\mathrm{1}−\mathrm{a}}{\mathrm{a}}\right)^{\mathrm{2}} −\frac{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} } \\ $$$$\:\mathrm{pq}+\mathrm{qr}+\mathrm{rp}=\frac{\left(\mathrm{1}−\mathrm{a}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{a}^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{2}} } \\ $$$$\mathrm{C}\Rightarrow\mathrm{p}^{\mathrm{3}} +\mathrm{q}^{\mathrm{3}} +\mathrm{r}^{\mathrm{3}} =\frac{\mathrm{3}−\mathrm{a}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{3}} } \\ $$$$\:\:\:\:\mathrm{p}^{\mathrm{3}} +\mathrm{q}^{\mathrm{3}} +\mathrm{r}^{\mathrm{3}} −\mathrm{3pqr}=\frac{\mathrm{3}−\mathrm{a}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{3}} }−\mathrm{3pqr} \\ $$$$\left(\mathrm{p}+\mathrm{q}+\mathrm{r}\right)\left(\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} −\left(\mathrm{pq}+\mathrm{qr}+\mathrm{rp}\right)\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}−\mathrm{a}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{3}} }−\mathrm{3pqr} \\ $$$$\mathrm{3pqr}=\frac{\mathrm{3}−\mathrm{a}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{3}} }−\left(\frac{\mathrm{1}−\mathrm{a}}{\mathrm{a}}\right)\left(\frac{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }−\frac{\left(\mathrm{1}−\mathrm{a}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{a}^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{pqr}=\frac{\mathrm{3}−\mathrm{a}^{\mathrm{3}} }{\mathrm{3a}^{\mathrm{3}} }−\left(\frac{\mathrm{1}−\mathrm{a}}{\mathrm{3a}}\right)\left(\frac{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }−\frac{\left(\mathrm{1}−\mathrm{a}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{a}^{\mathrm{2}} }{\mathrm{2a}^{\mathrm{2}} }\right) \\ $$

Commented by Tawa11 last updated on 23/Jul/21

Thanks sir. God bless you.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Answered by mr W last updated on 23/Jul/21

p_k =a^k +b^k +c^k +d^k e_1 =p_1 =1 2e_2 =e_1 p_1 −p_2 =1−2=−1 ⇒e_2 =−(1/2) 3e_3 =e_2 p_1 −e_1 p_2 +p_3 =−(1/2)−2+3=(1/2) ⇒e_3 =(1/6) 4e_4 =e_3 p_1 −e_2 p_2 +e_1 p_3 −p_4 =(1/6)+1+3−4=(1/6) ⇒e_4 =(1/(24)) 0=e_4 p_1 −e_3 p_2 +e_2 p_3 −e_1 p_4 +p_5 ⇒p_5 =−(1/(24))+(1/3)+(3/2)+4=((139)/(24)) 0=−e_4 p_2 +e_3 p_3 −e_2 p_4 +e_1 p_5 −p_6 ⇒p_6 =−(1/(12))+(1/2)+2+((139)/(24))=((197)/(24)) generally p_n =p_(n−1) +(p_(n−2) /2)+(p_(n−3) /6)−(p_(n−4) /(24)) or p_n =a^n +b^n +c^n +d^n a,b,c,d are roots of equation x^4 −x^3 −(1/2)x^2 −(1/6)x+(1/(24))=0

$${p}_{{k}} ={a}^{{k}} +{b}^{{k}} +{c}^{{k}} +{d}^{{k}} \\ $$$${e}_{\mathrm{1}} ={p}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{2}{e}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −{p}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}=−\mathrm{1}\:\Rightarrow{e}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3}{e}_{\mathrm{3}} ={e}_{\mathrm{2}} {p}_{\mathrm{1}} −{e}_{\mathrm{1}} {p}_{\mathrm{2}} +{p}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}+\mathrm{3}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{e}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{4}{e}_{\mathrm{4}} ={e}_{\mathrm{3}} {p}_{\mathrm{1}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{1}} {p}_{\mathrm{3}} −{p}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{6}}+\mathrm{1}+\mathrm{3}−\mathrm{4}=\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow{e}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{24}} \\ $$$$\mathrm{0}={e}_{\mathrm{4}} {p}_{\mathrm{1}} −{e}_{\mathrm{3}} {p}_{\mathrm{2}} +{e}_{\mathrm{2}} {p}_{\mathrm{3}} −{e}_{\mathrm{1}} {p}_{\mathrm{4}} +{p}_{\mathrm{5}} \: \\ $$$$\Rightarrow{p}_{\mathrm{5}} =−\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{4}=\frac{\mathrm{139}}{\mathrm{24}} \\ $$$$\mathrm{0}=−{e}_{\mathrm{4}} {p}_{\mathrm{2}} +{e}_{\mathrm{3}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{4}} +{e}_{\mathrm{1}} {p}_{\mathrm{5}} −{p}_{\mathrm{6}} \: \\ $$$$\Rightarrow{p}_{\mathrm{6}} =−\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}+\frac{\mathrm{139}}{\mathrm{24}}=\frac{\mathrm{197}}{\mathrm{24}} \\ $$$$ \\ $$$${generally} \\ $$$${p}_{{n}} ={p}_{{n}−\mathrm{1}} +\frac{{p}_{{n}−\mathrm{2}} }{\mathrm{2}}+\frac{{p}_{{n}−\mathrm{3}} }{\mathrm{6}}−\frac{{p}_{{n}−\mathrm{4}} }{\mathrm{24}} \\ $$$${or} \\ $$$${p}_{{n}} ={a}^{{n}} +{b}^{{n}} +{c}^{{n}} +{d}^{{n}} \\ $$$${a},{b},{c},{d}\:{are}\:{roots}\:{of}\:{equation} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{x}+\frac{\mathrm{1}}{\mathrm{24}}=\mathrm{0} \\ $$

Commented by Tawa11 last updated on 23/Jul/21

Thanks sir. God bless you.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Commented by mr W last updated on 23/Jul/21

https://en.m.wikipedia.org/wiki/Newton%27s_identities

Commented by Rasheed.Sindhi last updated on 23/Jul/21

Wonderful method sir! But I′m feeling difficulity in understanding.

$$\mathcal{W}{onderful}\:{method}\:\boldsymbol{{sir}}! \\ $$$$\mathcal{B}{ut}\:{I}'{m}\:{feeling}\:\:{difficulity}\:{in} \\ $$$${understanding}. \\ $$

Commented by mr W last updated on 23/Jul/21

see also Q74970

$${see}\:{also}\:{Q}\mathrm{74970} \\ $$

Commented by Tawa11 last updated on 23/Jul/21

Sir, which sequence you use to get the P_n . Just the sequence.

$$\mathrm{Sir},\:\mathrm{which}\:\mathrm{sequence}\:\mathrm{you}\:\mathrm{use}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\:\mathrm{P}_{\mathrm{n}} .\:\mathrm{Just}\:\mathrm{the}\:\mathrm{sequence}. \\ $$

Commented by Tawa11 last updated on 23/Jul/21

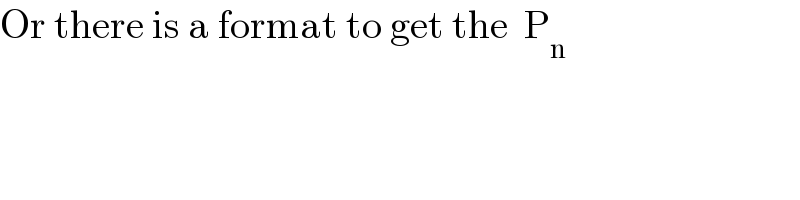
Or there is a format to get the P_n

$$\mathrm{Or}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{format}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\:\mathrm{P}_{\mathrm{n}} \\ $$

Commented by Tawa11 last updated on 24/Jul/21

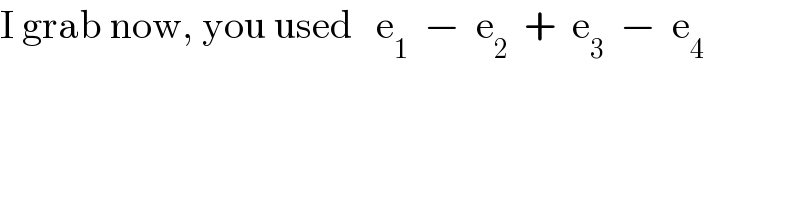
I grab now, you used e_1 − e_2 + e_3 − e_4

$$\mathrm{I}\:\mathrm{grab}\:\mathrm{now},\:\mathrm{you}\:\mathrm{used}\:\:\:\mathrm{e}_{\mathrm{1}} \:\:−\:\:\mathrm{e}_{\mathrm{2}} \:\:+\:\:\mathrm{e}_{\mathrm{3}} \:\:−\:\:\mathrm{e}_{\mathrm{4}} \\ $$

Commented by peter frank last updated on 24/Jul/21

thank you

$$\:{thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com