Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 147795 by ajfour last updated on 23/Jul/21

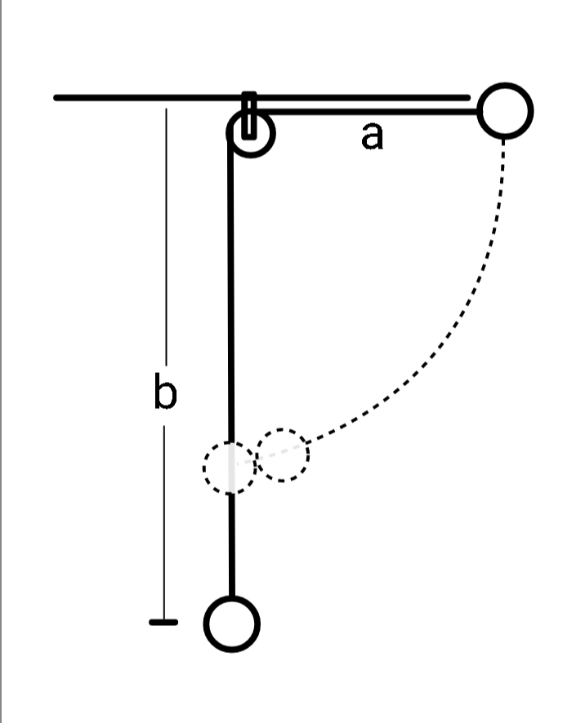
Commented by ajfour last updated on 23/Jul/21

$F i n d b / a .$
Commented by mr W last updated on 24/Jul/21

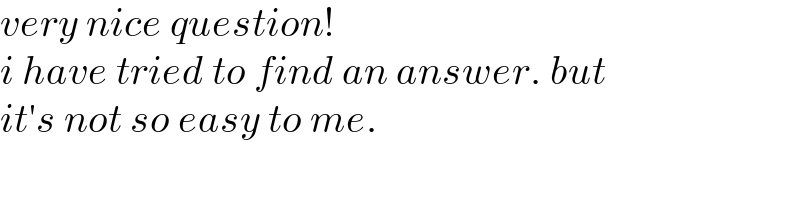
$v e r y n i c e q u e s t i o n!$ $i h a v e t r i e d t o f i n d a n a n s w e r . b u t$ ${i t}^{'} s n o t s o e a s y t o m e .$
	Answered by mr W last updated on 23/Jul/21

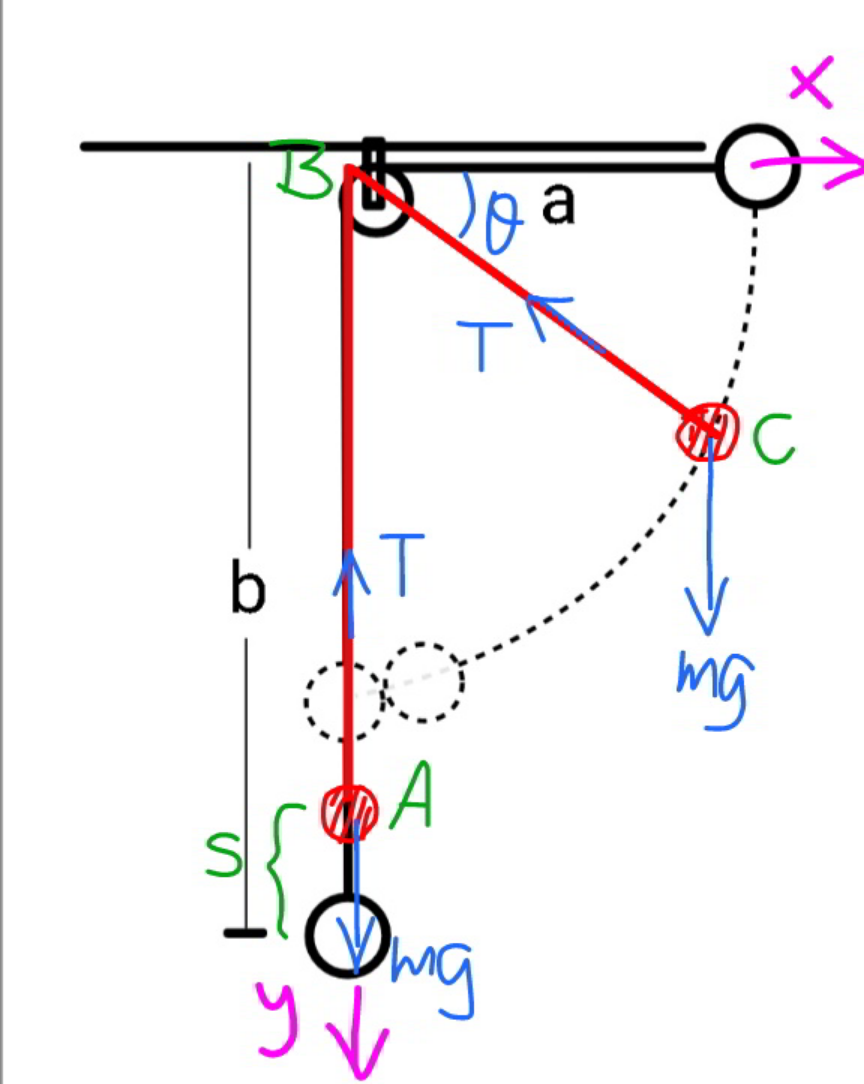
	Commented by mr W last updated on 24/Jul/21

	$y_{A} = b - s$ $x_{C} = (a + s) \cos θ$ $y_{C} = (a + s) \sin θ$ $ω = \frac{d θ}{d t}$ $u = \frac{d s}{d t}$ $u_{A} = - \frac{{d y}_{A}}{d t} = u$ $a_{A} = \frac{{d u}_{A}}{d t} = \frac{d u}{d t}$ $T - m g = {m a}_{A}$ $\Rightarrow T = m (a_{A} + g)$ $u_{C x} = - \frac{{d x}_{C}}{d t} = (a + s) ω \sin θ - u \cos θ$ $a_{C x} = u ω \sin θ + (a + s) α \sin θ + (a + s) ω^{2} \cos θ - a_{A} \cos θ + u ω \sin θ$ $u_{C y} = \frac{{d y}_{C}}{d t} = (a + s) ω \cos θ + u \sin θ$ $a_{C y} = u ω \cos θ + (a + s) α \cos θ - (a + s) ω^{2} \sin θ + a_{A} \sin θ + u ω \cos θ$ $\frac{1}{2} m [u^{2} + {(a + s)}^{2} ω^{2} \sin^{2} θ + u^{2} \cos^{2} θ - 2 (a + s) ω u \sin θ \cos θ + {(a + s)}^{2} ω^{2} \cos^{2} θ + u^{2} \sin^{2} θ + 2 (a + s) ω u \cos θ \sin θ] = m g [(a + s) \sin θ - s]$ $\Rightarrow 2 u^{2} + {(a + s)}^{2} ω^{2} = 2 g [(a + s) \sin θ - s] . . . (i)$ $T \cos θ = {m a}_{C x}$ $(a_{A} + g) \cos θ = u ω \sin θ + (a + s) α \sin θ + (a + s) ω^{2} \cos θ - a_{A} \cos θ + u ω \sin θ$ $\Rightarrow 2 a_{A} + g = 2 u ω \tan θ + (a + s) α \tan θ + (a + s) ω^{2}$ $m g - T \sin θ = {m a}_{C y}$ $\Rightarrow 2 a_{A} + g = \frac{1}{\tan θ} [g - 2 u ω - (a + s) α] + (a + s) ω^{2}$ $2 u ω \tan θ + (a + s) α \tan θ + (a + s) ω^{2} = \frac{1}{\tan θ} [g - 2 u ω - (a + s) α] + (a + s) ω^{2}$ $[2 u ω + (a + s) α] (1 + \tan^{2} θ) = g$ $\Rightarrow 2 u ω + (a + s) α = g \cos^{2} θ . . . (i i)$ $α = \frac{d ω}{d t} = ω \frac{d ω}{d θ}$ $f r o m (i) :$ $u = \sqrt{g [(a + s) \sin θ - s] - \frac{1}{2} {(a + s)}^{2} ω^{2}}$ $\Rightarrow \frac{d s}{d θ} = \frac{1}{ω} \sqrt{g [(a + s) \sin θ - s] - \frac{1}{2} {(a + s)}^{2} ω^{2}}$ $f r o m (i i) :$ $\Rightarrow \frac{d ω}{d θ} = \frac{g \cos^{2} θ}{ω (a + s)} - \frac{2}{a + s} \sqrt{g [(a + s) \sin θ - s] - \frac{1}{2} {(a + s)}^{2} ω^{2}}$ $. . . . . .$ $s (θ) ∣_{θ = 0} = 0$ $ω (θ) ∣_{θ = 0} = 0$ $s (θ) ∣_{θ = \frac{π}{2}} = \frac{b - a}{2}$
	Commented by ajfour last updated on 25/Jul/21
	$mgrcos θ=(mr^2 )((ωdω)/dθ) ...(i) mgrsin θ=(1/2)m(v^2 +v^2 ) +(1/2)m(ωr)^2 +mg(a+b−r) ..(ii) v=(dr/dt)=((ωdr)/dθ) ...(iii) L=a+b ⇒ 2g(rsin θ+r−L) =2(((ωdr)/dθ))^2 +(ωr)^2 ⇒ ω^2 =((2g(rsin θ+r−L))/(2((dr/dθ))^2 +r^2 )) ((2ωdω)/dθ)=((2g((dr/dθ)sin θ+rcos θ+(dr/dθ)){2((dr/dθ))^2 +r^2 }−2g(rsin θ+r−L){4((dr/dθ))((d^2 r/dθ^2 ))+2r((dr/dθ))^2 })/({2((dr/dθ))^2 +r^2 }^2 )) =((2gcos θ)/r) ⇒ (((rdr)/dθ))(1+sin θ) +r^2 cos θ{2((dr/dθ))^2 +r^2 } −(r^2 sin θ+r^2 −Lr){4((dr/dθ))((d^2 r/dθ^2 ))+2r((dr/dθ))^2 } = cos θ{2((dr/dθ))^2 +r^2 }^2 difficult D.E. , sir.$
	$m g r \cos θ = ({m r}^{2}) \frac{ω d ω}{d θ} . . . (i)$ $m g r \sin θ = \frac{1}{2} m (v^{2} + v^{2})$ $+ \frac{1}{2} m {(ω r)}^{2} + m g (a + b - r) . . (i i)$ $v = \frac{d r}{d t} = \frac{ω d r}{d θ} . . . (i i i)$ $L = a + b$ $\Rightarrow$ $2 g (r \sin θ + r - L)$ $= 2 {(\frac{ω d r}{d θ})}^{2} + {(ω r)}^{2}$ $\Rightarrow ω^{2} = \frac{2 g (r \sin θ + r - L)}{2 {(\frac{d r}{d θ})}^{2} + r^{2}}$ $\frac{2 ω d ω}{d θ} = \frac{2 g (\frac{d r}{d θ} \sin θ + r \cos θ + \frac{d r}{d θ}) {2 {(\frac{d r}{d θ})}^{2} + r^{2}} - 2 g (r \sin θ + r - L) {4 (\frac{d r}{d θ}) (\frac{d^{2} r}{d θ^{2}}) + 2 r {(\frac{d r}{d θ})}^{2}}}{{2 {(\frac{d r}{d θ})}^{2} + r^{2}}^{2}}$ $= \frac{2 g \cos θ}{r}$ $\Rightarrow$ $(\frac{r d r}{d θ}) (1 + \sin θ)$ $+ r^{2} \cos θ {2 {(\frac{d r}{d θ})}^{2} + r^{2}}$ $- (r^{2} \sin θ + r^{2} - L r) {4 (\frac{d r}{d θ}) (\frac{d^{2} r}{d θ^{2}}) + 2 r {(\frac{d r}{d θ})}^{2}}$ $= \cos θ {2 {(\frac{d r}{d θ})}^{2} + r^{2}}^{2}$ $d i f f i c u l t D . E ., s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum