Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 147971 by mathmax by abdo last updated on 24/Jul/21

find ∫_(−∞) ^(+∞) ((x^3 dx)/((x^2 +x+1)^4 ))

$$\mathrm{find}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{3}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$

Commented by tabata last updated on 24/Jul/21

msr abdo can help me in question 147915 plese ?

$${msr}\:{abdo}\:{can}\:{help}\:{me}\:{in}\:{question}\:\mathrm{147915}\:{plese}\:? \\ $$

Commented by mathmax by abdo last updated on 24/Jul/21

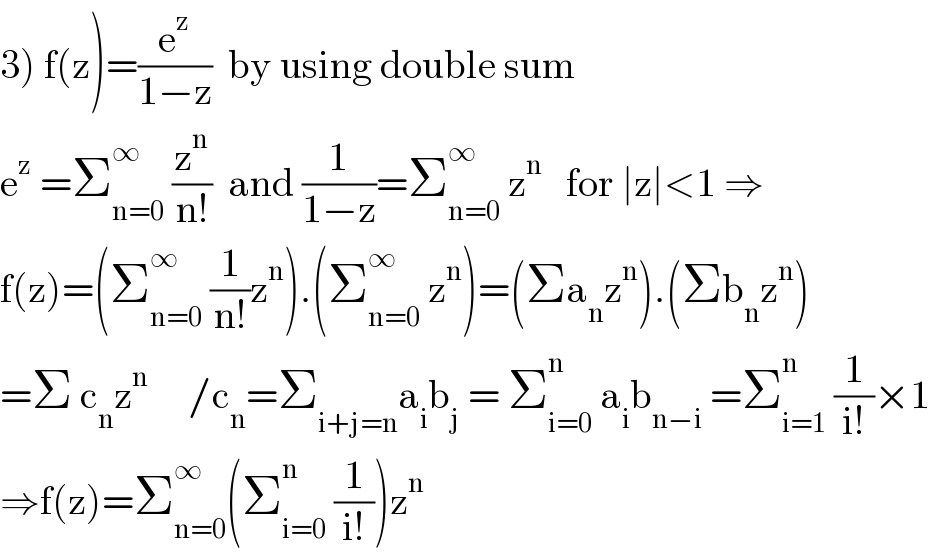
3) f(z)=(e^z /(1−z)) by using double sum e^z =Σ_(n=0) ^∞ (z^n /(n!)) and (1/(1−z))=Σ_(n=0) ^∞ z^n for ∣z∣<1 ⇒ f(z)=(Σ_(n=0) ^∞ (1/(n!))z^n ).(Σ_(n=0) ^∞ z^n )=(Σa_n z^n ).(Σb_n z^n ) =Σ c_n z^n /c_n =Σ_(i+j=n) a_i b_j = Σ_(i=0) ^n a_i b_(n−i) =Σ_(i=1) ^n (1/(i!))×1 ⇒f(z)=Σ_(n=0) ^∞ (Σ_(i=0) ^n (1/(i!)))z^n

$$\left.\mathrm{3}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{z}} }{\mathrm{1}−\mathrm{z}}\:\:\mathrm{by}\:\mathrm{using}\:\mathrm{double}\:\mathrm{sum} \\ $$$$\mathrm{e}^{\mathrm{z}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{n}!}\:\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{n}} \:\:\:\mathrm{for}\:\mid\mathrm{z}\mid<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}!}\mathrm{z}^{\mathrm{n}} \right).\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{n}} \right)=\left(\Sigma\mathrm{a}_{\mathrm{n}} \mathrm{z}^{\mathrm{n}} \right).\left(\Sigma\mathrm{b}_{\mathrm{n}} \mathrm{z}^{\mathrm{n}} \right) \\ $$$$=\Sigma\:\mathrm{c}_{\mathrm{n}} \mathrm{z}^{\mathrm{n}} \:\:\:\:\:/\mathrm{c}_{\mathrm{n}} =\sum_{\mathrm{i}+\mathrm{j}=\mathrm{n}} \mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{j}} \:=\:\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{n}−\mathrm{i}} \:=\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{i}!}×\mathrm{1} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{i}!}\right)\mathrm{z}^{\mathrm{n}} \\ $$

Commented by mathmax by abdo last updated on 24/Jul/21

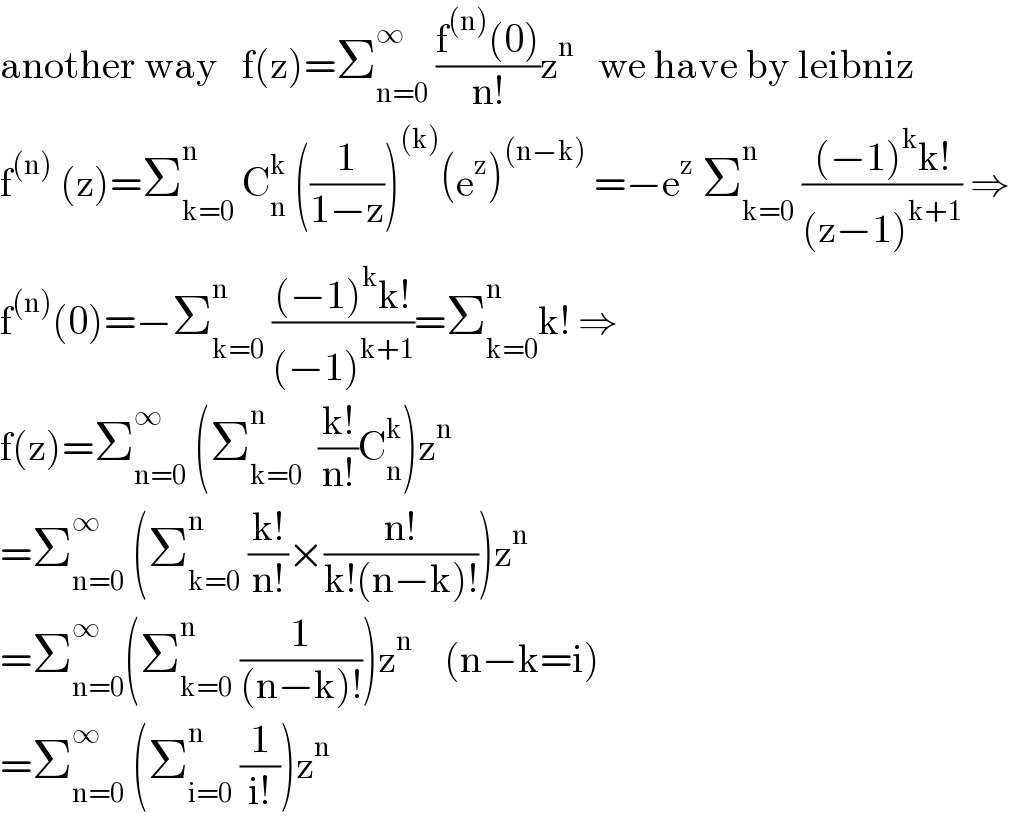
another way f(z)=Σ_(n=0) ^∞ ((f^((n)) (0))/(n!))z^n we have by leibniz f^((n)) (z)=Σ_(k=0) ^n C_n ^k ((1/(1−z)))^((k)) (e^z )^((n−k)) =−e^z Σ_(k=0) ^n (((−1)^k k!)/((z−1)^(k+1) )) ⇒ f^((n)) (0)=−Σ_(k=0) ^n (((−1)^k k!)/((−1)^(k+1) ))=Σ_(k=0) ^n k! ⇒ f(z)=Σ_(n=0) ^∞ (Σ_(k=0) ^n ((k!)/(n!))C_n ^k )z^n =Σ_(n=0) ^∞ (Σ_(k=0) ^n ((k!)/(n!))×((n!)/(k!(n−k)!)))z^n =Σ_(n=0) ^∞ (Σ_(k=0) ^n (1/((n−k)!)))z^n (n−k=i) =Σ_(n=0) ^∞ (Σ_(i=0) ^n (1/(i!)))z^n

$$\mathrm{another}\:\mathrm{way}\:\:\:\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\mathrm{z}^{\mathrm{n}} \:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{by}\:\mathrm{leibniz} \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \:\left(\mathrm{z}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}\right)^{\left(\mathrm{k}\right)} \left(\mathrm{e}^{\mathrm{z}} \right)^{\left(\mathrm{n}−\mathrm{k}\right)} \:=−\mathrm{e}^{\mathrm{z}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{k}!}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)=−\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{k}!}{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} }=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{k}!\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\:\frac{\mathrm{k}!}{\mathrm{n}!}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \right)\mathrm{z}^{\mathrm{n}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{k}!}{\mathrm{n}!}×\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!}\right)\mathrm{z}^{\mathrm{n}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{k}\right)!}\right)\mathrm{z}^{\mathrm{n}} \:\:\:\:\left(\mathrm{n}−\mathrm{k}=\mathrm{i}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{i}!}\right)\mathrm{z}^{\mathrm{n}} \\ $$

Commented by mathmax by abdo last updated on 24/Jul/21

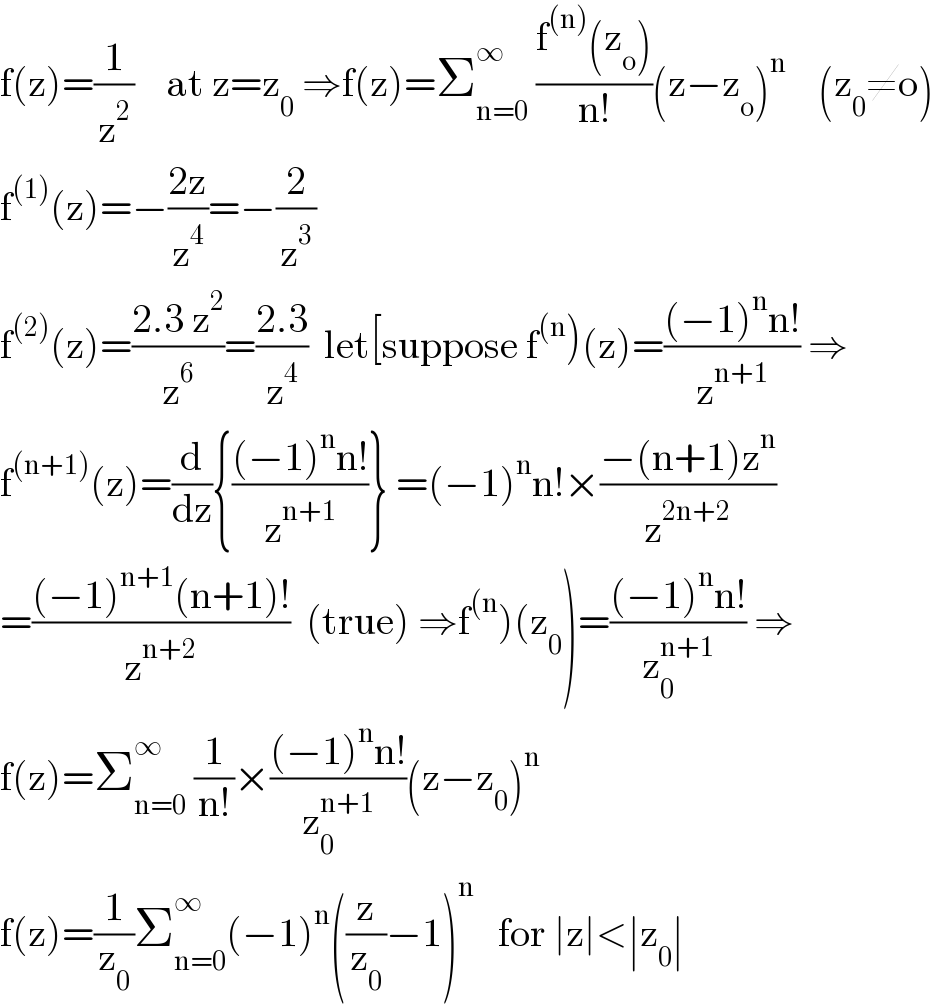
f(z)=(1/z^2 ) at z=z_0 ⇒f(z)=Σ_(n=0) ^∞ ((f^((n)) (z_o ))/(n!))(z−z_o )^n (z_0 ≠o) f^((1)) (z)=−((2z)/z^4 )=−(2/z^3 ) f^((2)) (z)=((2.3 z^2 )/z^6 )=((2.3)/z^4 ) let[suppose f^((n) )(z)=(((−1)^n n!)/z^(n+1) ) ⇒ f^((n+1)) (z)=(d/dz){(((−1)^n n!)/z^(n+1) )} =(−1)^n n!×((−(n+1)z^n )/z^(2n+2) ) =(((−1)^(n+1) (n+1)!)/z^(n+2) ) (true) ⇒f^((n) )(z_0 )=(((−1)^n n!)/z_0 ^(n+1) ) ⇒ f(z)=Σ_(n=0) ^∞ (1/(n!))×(((−1)^n n!)/z_0 ^(n+1) )(z−z_0 )^n f(z)=(1/z_0 )Σ_(n=0) ^∞ (−1)^n ((z/z_0 )−1)^n for ∣z∣<∣z_0 ∣

$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\:\:\:\:\mathrm{at}\:\mathrm{z}=\mathrm{z}_{\mathrm{0}} \:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{z}_{\mathrm{o}} \right)}{\mathrm{n}!}\left(\mathrm{z}−\mathrm{z}_{\mathrm{o}} \right)^{\mathrm{n}} \:\:\:\:\left(\mathrm{z}_{\mathrm{0}} \neq\mathrm{o}\right) \\ $$$$\mathrm{f}^{\left(\mathrm{1}\right)} \left(\mathrm{z}\right)=−\frac{\mathrm{2z}}{\mathrm{z}^{\mathrm{4}} }=−\frac{\mathrm{2}}{\mathrm{z}^{\mathrm{3}} } \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{z}\right)=\frac{\mathrm{2}.\mathrm{3}\:\mathrm{z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{6}} }=\frac{\mathrm{2}.\mathrm{3}}{\mathrm{z}^{\mathrm{4}} }\:\:\mathrm{let}\left[\mathrm{suppose}\:\mathrm{f}^{\left(\mathrm{n}\right.} \right)\left(\mathrm{z}\right)=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\mathrm{z}^{\mathrm{n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}+\mathrm{1}\right)} \left(\mathrm{z}\right)=\frac{\mathrm{d}}{\mathrm{dz}}\left\{\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\mathrm{z}^{\mathrm{n}+\mathrm{1}} }\right\}\:=\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!×\frac{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{z}^{\mathrm{n}} }{\mathrm{z}^{\mathrm{2n}+\mathrm{2}} } \\ $$$$\left.=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \left(\mathrm{n}+\mathrm{1}\right)!}{\mathrm{z}^{\mathrm{n}+\mathrm{2}} }\:\:\left(\mathrm{true}\right)\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right.} \right)\left(\mathrm{z}_{\mathrm{0}} \right)=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\mathrm{z}_{\mathrm{0}} ^{\mathrm{n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}!}×\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{n}!}{\mathrm{z}_{\mathrm{0}} ^{\mathrm{n}+\mathrm{1}} }\left(\mathrm{z}−\mathrm{z}_{\mathrm{0}} \right)^{\mathrm{n}} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{0}} }\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\mathrm{z}}{\mathrm{z}_{\mathrm{0}} }−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\mathrm{for}\:\mid\mathrm{z}\mid<\mid\mathrm{z}_{\mathrm{0}} \mid \\ $$

Commented by tabata last updated on 25/Jul/21

thank you msr mathmax by abd thank you very much msr are you there tomorrow at 12 oclock at after noon ?

$${thank}\:{you}\:{msr}\:{mathmax}\:{by}\:{abd}\:{thank}\:{you} \\ $$$${very}\:{much}\: \\ $$$$ \\ $$$${msr}\:{are}\:{you}\:{there}\:{tomorrow}\:{at}\:\mathrm{12}\:{oclock} \\ $$$${at}\:{after}\:{noon}\:? \\ $$

Commented by mathmax by abdo last updated on 25/Jul/21

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com