
Question and Answers Forum
Question Number 147992 by Sozan last updated on 24/Jul/21
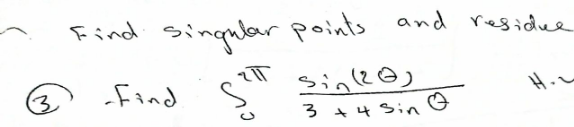
Commented by Sozan last updated on 25/Jul/21
Answered by mathmax by abdo last updated on 25/Jul/21
![Ψ=∫_0 ^(2π) ((sin(2x))/(3+4sinx)) ⇒Ψ=∫_0 ^(2π) ((2sinx.cosx)/(3+4sinx))dx =_(e^(ix) =z) ∫_(∣z∣=1) ((2((z−z^(−1) )/(2i)).((z+z^(−1) )/2))/(3+4((z−z^(−1) )/(2i)))) (dz/(iz)) =∫_(∣z∣=1) ((z^2 −z^(−2) )/(iz(6i+4z−4z^(−1) )))dz =−i∫_(∣z∣=1) ((z^2 −z^(−2) )/(6iz+4z^2 −4))dz =−(i/2)∫_(∣z∣=1) ((z^2 −z^(−2) )/(2z^2 +3iz−2))dz let ϕ(z)=((z^2 −z^(−2) )/(2z^2 +3iz−2)) poles? Δ=−9−4(−4) =16−9=7 ⇒z_1 =((−3i+(√7))/4) z_2 =((−3i−(√7))/4) ∣z_1 ∣−1 =(1/4)(√(9+7))−1 =0 ⇒∣z_1 ∣=1 z_1 z_2 =1 ⇒∣z_2 ∣=1 residus ⇒∫_(∣z∣=1) ϕ(z)dz=2iπ{Res(ϕ,z_1 )+Res(ϕ,z_2 )} but Re(ϕ,z_2 )=−Res(ϕ,z_1 )⇒∫_(∣z∣=1) ϕ(z)dz=0 ⇒Ψ=0 another way Ψ=∫_0 ^π ()dx +∫_π ^(2π) ()dx =_(x=π+α) ∫_0 ^π ((sin2x)/(3+4sinx))dx +∫_0 ^π ((sin(2α))/(3−4sinα))dα =∫_0 ^π sin(2x){(1/(3+4sinx))+(1/(3−4sinx))}dx =∫_0 ^π ((6sin(2x))/(9−16sin^2 x))dx =∫_0 ^π ((6sin(2x))/(9−16(1−cos^2 x)))dx =∫_0 ^π ((6sin(2x))/(16cos^2 x−7))dx =∫_0 ^π ((6sin(2x))/(16.((1+cos(2x))/2)−7))dx =∫_0 ^π ((6sin(2x))/(1+8cos(2x)))dx =(6/(16))∫_0 ^π ((16sin(2x))/(8cos(2x)+1))dx =(3/8)[ln∣8cos(2x)+1∣]_0 ^π =(3/8){ln9−log9}=0](Q148006.png)
Commented by tabata last updated on 25/Jul/21
| ||
Question and Answers Forum | ||
Question Number 147992 by Sozan last updated on 24/Jul/21 | ||
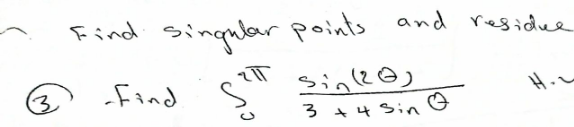 | ||
Commented by Sozan last updated on 25/Jul/21 | ||
 | ||
Answered by mathmax by abdo last updated on 25/Jul/21 | ||
![Ψ=∫_0 ^(2π) ((sin(2x))/(3+4sinx)) ⇒Ψ=∫_0 ^(2π) ((2sinx.cosx)/(3+4sinx))dx =_(e^(ix) =z) ∫_(∣z∣=1) ((2((z−z^(−1) )/(2i)).((z+z^(−1) )/2))/(3+4((z−z^(−1) )/(2i)))) (dz/(iz)) =∫_(∣z∣=1) ((z^2 −z^(−2) )/(iz(6i+4z−4z^(−1) )))dz =−i∫_(∣z∣=1) ((z^2 −z^(−2) )/(6iz+4z^2 −4))dz =−(i/2)∫_(∣z∣=1) ((z^2 −z^(−2) )/(2z^2 +3iz−2))dz let ϕ(z)=((z^2 −z^(−2) )/(2z^2 +3iz−2)) poles? Δ=−9−4(−4) =16−9=7 ⇒z_1 =((−3i+(√7))/4) z_2 =((−3i−(√7))/4) ∣z_1 ∣−1 =(1/4)(√(9+7))−1 =0 ⇒∣z_1 ∣=1 z_1 z_2 =1 ⇒∣z_2 ∣=1 residus ⇒∫_(∣z∣=1) ϕ(z)dz=2iπ{Res(ϕ,z_1 )+Res(ϕ,z_2 )} but Re(ϕ,z_2 )=−Res(ϕ,z_1 )⇒∫_(∣z∣=1) ϕ(z)dz=0 ⇒Ψ=0 another way Ψ=∫_0 ^π ()dx +∫_π ^(2π) ()dx =_(x=π+α) ∫_0 ^π ((sin2x)/(3+4sinx))dx +∫_0 ^π ((sin(2α))/(3−4sinα))dα =∫_0 ^π sin(2x){(1/(3+4sinx))+(1/(3−4sinx))}dx =∫_0 ^π ((6sin(2x))/(9−16sin^2 x))dx =∫_0 ^π ((6sin(2x))/(9−16(1−cos^2 x)))dx =∫_0 ^π ((6sin(2x))/(16cos^2 x−7))dx =∫_0 ^π ((6sin(2x))/(16.((1+cos(2x))/2)−7))dx =∫_0 ^π ((6sin(2x))/(1+8cos(2x)))dx =(6/(16))∫_0 ^π ((16sin(2x))/(8cos(2x)+1))dx =(3/8)[ln∣8cos(2x)+1∣]_0 ^π =(3/8){ln9−log9}=0](Q148006.png) | ||
| ||
Commented by tabata last updated on 25/Jul/21 | ||
 | ||