
Question and Answers Forum
Question Number 148000 by vvvv last updated on 25/Jul/21
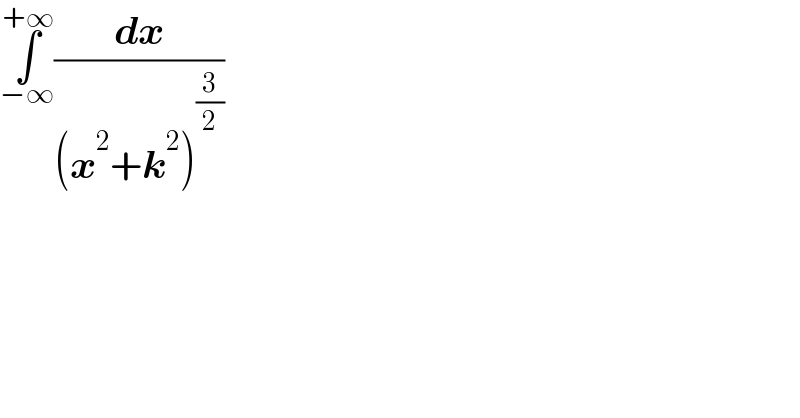
Answered by gsk2684 last updated on 25/Jul/21
![2∫_(x=0) ^∞ (dx/(x^3 (1+(k^2 /x^2 ))^(3/2) )) changement 1+(k^2 /x^2 )=t ⇒ −((2k^2 )/x^3 )dx=dt 2∫_(t=∞) ^1 t^(−(3/2)) (dt/(−2k^2 ))=((−1)/k^2 )[(t^(((−3)/2)+1) /(−(3/2)+1))]_∞ ^1 =((−1)/k^2 )[(t^(−(1/2)) /(−(1/2)))]_∞ ^1 =(2/k^2 )[(1/( (√t)))]_∞ ^1 =(2/k^2 )[1−0]=(2/k^2 )](Q148002.png)
Answered by mathmax by abdo last updated on 25/Jul/21
![U_k =∫_(−∞) ^(+∞) (dx/((x^2 +k^2 )^(3/2) )) changement x=ktanθ give U_k =∫_(−(π/2)) ^(π/2) ((k(1+tan^2 θ))/(k^3 (1+tan^2 θ)^(3/2) ))dθ =(1/k^2 )∫_(−(π/2)) ^(π/2) (dθ/( (√(1+tan^2 θ)))) =(1/k^2 )∫_(−(π/2)) ^(π/2) cosθ dθ =(1/k^2 )[sinθ]_(−(π/2)) ^(π/2) =(1/k^2 )(1−(−1)) =(2/k^2 ) (k≠0)](Q148003.png)
| ||
Question and Answers Forum | ||
Question Number 148000 by vvvv last updated on 25/Jul/21 | ||
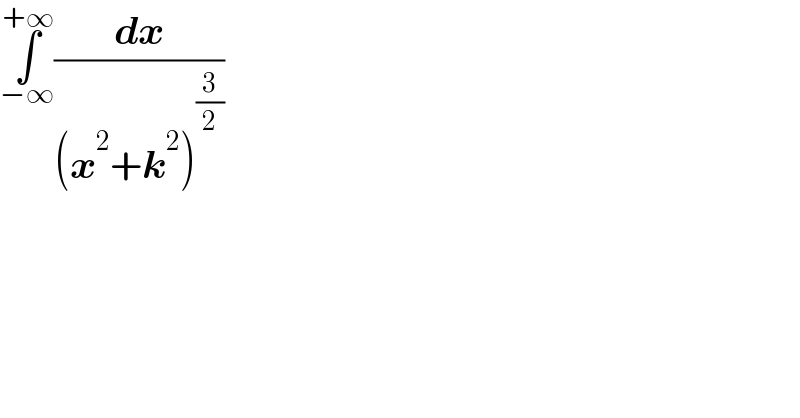 | ||
Answered by gsk2684 last updated on 25/Jul/21 | ||
![2∫_(x=0) ^∞ (dx/(x^3 (1+(k^2 /x^2 ))^(3/2) )) changement 1+(k^2 /x^2 )=t ⇒ −((2k^2 )/x^3 )dx=dt 2∫_(t=∞) ^1 t^(−(3/2)) (dt/(−2k^2 ))=((−1)/k^2 )[(t^(((−3)/2)+1) /(−(3/2)+1))]_∞ ^1 =((−1)/k^2 )[(t^(−(1/2)) /(−(1/2)))]_∞ ^1 =(2/k^2 )[(1/( (√t)))]_∞ ^1 =(2/k^2 )[1−0]=(2/k^2 )](Q148002.png) | ||
| ||
Answered by mathmax by abdo last updated on 25/Jul/21 | ||
![U_k =∫_(−∞) ^(+∞) (dx/((x^2 +k^2 )^(3/2) )) changement x=ktanθ give U_k =∫_(−(π/2)) ^(π/2) ((k(1+tan^2 θ))/(k^3 (1+tan^2 θ)^(3/2) ))dθ =(1/k^2 )∫_(−(π/2)) ^(π/2) (dθ/( (√(1+tan^2 θ)))) =(1/k^2 )∫_(−(π/2)) ^(π/2) cosθ dθ =(1/k^2 )[sinθ]_(−(π/2)) ^(π/2) =(1/k^2 )(1−(−1)) =(2/k^2 ) (k≠0)](Q148003.png) | ||
| ||