Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148068 by tabata last updated on 25/Jul/21

Answered by Olaf_Thorendsen last updated on 25/Jul/21

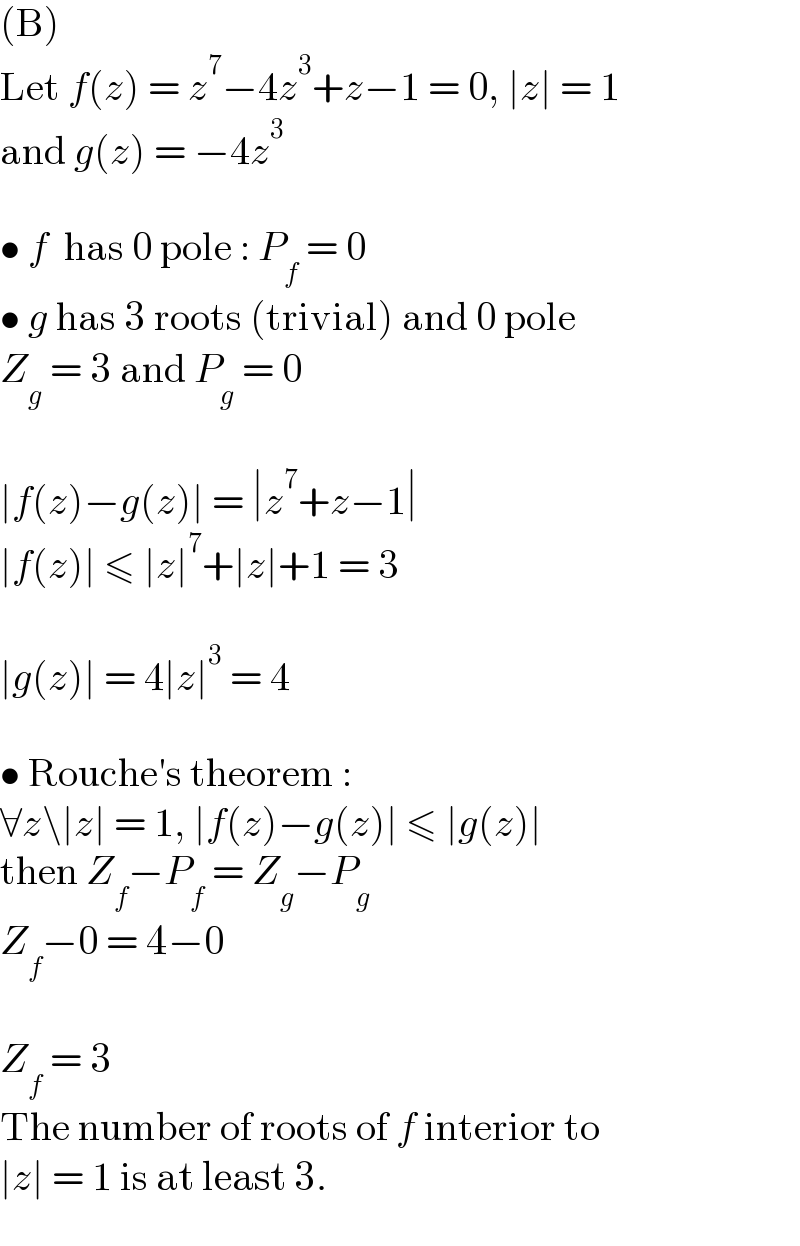
(B) Let f(z) = z^7 −4z^3 +z−1 = 0, ∣z∣ = 1 and g(z) = −4z^3 • f has 0 pole : P_f = 0 • g has 3 roots (trivial) and 0 pole Z_g = 3 and P_g = 0 ∣f(z)−g(z)∣ = ∣z^7 +z−1∣ ∣f(z)∣ ≤ ∣z∣^7 +∣z∣+1 = 3 ∣g(z)∣ = 4∣z∣^3 = 4 • Rouche′s theorem : ∀z\∣z∣ = 1, ∣f(z)−g(z)∣ ≤ ∣g(z)∣ then Z_f −P_f = Z_g −P_g Z_f −0 = 4−0 Z_f = 3 The number of roots of f interior to ∣z∣ = 1 is at least 3.

$$\left(\mathrm{B}\right) \\ $$$$\mathrm{Let}\:{f}\left({z}\right)\:=\:{z}^{\mathrm{7}} −\mathrm{4}{z}^{\mathrm{3}} +{z}−\mathrm{1}\:=\:\mathrm{0},\:\mid{z}\mid\:=\:\mathrm{1} \\ $$$$\mathrm{and}\:{g}\left({z}\right)\:=\:−\mathrm{4}{z}^{\mathrm{3}} \\ $$$$ \\ $$$$\bullet\:{f}\:\:\mathrm{has}\:\mathrm{0}\:\mathrm{pole}\::\:{P}_{{f}} \:=\:\mathrm{0} \\ $$$$\bullet\:{g}\:\mathrm{has}\:\mathrm{3}\:\mathrm{roots}\:\left(\mathrm{trivial}\right)\:\mathrm{and}\:\mathrm{0}\:\mathrm{pole} \\ $$$${Z}_{{g}} \:=\:\mathrm{3}\:\mathrm{and}\:{P}_{{g}} \:=\:\mathrm{0} \\ $$$$ \\ $$$$\mid{f}\left({z}\right)−{g}\left({z}\right)\mid\:=\:\mid{z}^{\mathrm{7}} +{z}−\mathrm{1}\mid\: \\ $$$$\mid{f}\left({z}\right)\mid\:\leqslant\:\mid{z}\mid^{\mathrm{7}} +\mid{z}\mid+\mathrm{1}\:=\:\mathrm{3} \\ $$$$ \\ $$$$\mid{g}\left({z}\right)\mid\:=\:\mathrm{4}\mid{z}\mid^{\mathrm{3}} \:=\:\mathrm{4} \\ $$$$ \\ $$$$\bullet\:\mathrm{Rouche}'\mathrm{s}\:\mathrm{theorem}\:: \\ $$$$\forall{z}\backslash\mid{z}\mid\:=\:\mathrm{1},\:\mid{f}\left({z}\right)−{g}\left({z}\right)\mid\:\leqslant\:\mid{g}\left({z}\right)\mid \\ $$$$\mathrm{then}\:{Z}_{{f}} −{P}_{{f}} \:=\:{Z}_{{g}} −{P}_{{g}} \\ $$$${Z}_{{f}} −\mathrm{0}\:=\:\mathrm{4}−\mathrm{0} \\ $$$$ \\ $$$${Z}_{{f}} \:=\:\mathrm{3} \\ $$$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{roots}\:\mathrm{of}\:{f}\:\mathrm{interior}\:\mathrm{to} \\ $$$$\mid{z}\mid\:=\:\mathrm{1}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{3}. \\ $$

Commented by tabata last updated on 25/Jul/21

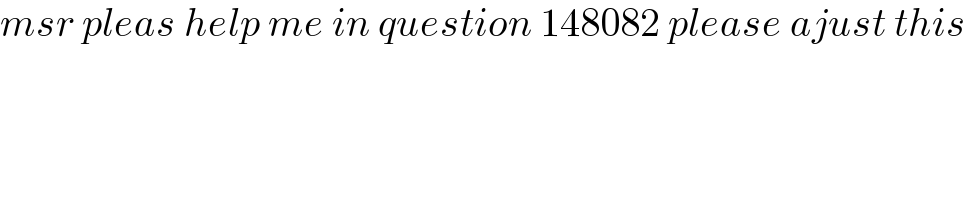
msr pleas help me in question 148082 please ajust this

$${msr}\:{pleas}\:{help}\:{me}\:{in}\:{question}\:\mathrm{148082}\:{please}\:{ajust}\:{this} \\ $$

Answered by Olaf_Thorendsen last updated on 25/Jul/21

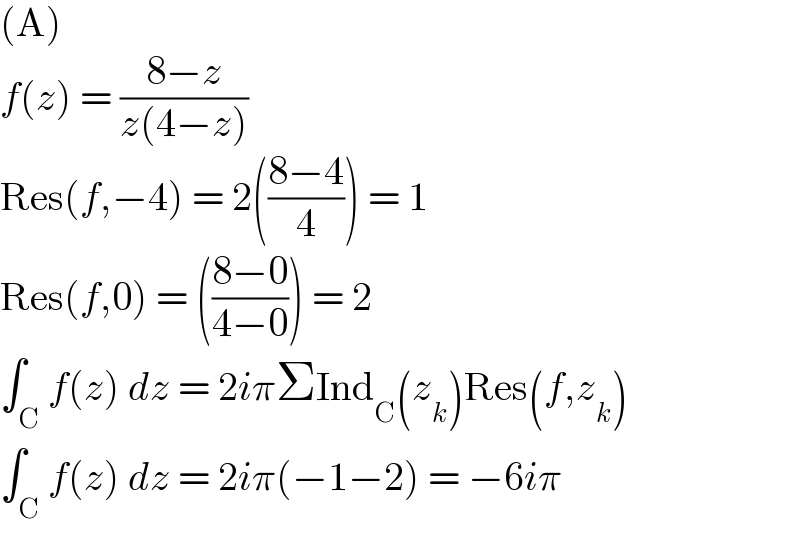
(A) f(z) = ((8−z)/(z(4−z))) Res(f,−4) = 2(((8−4)/4)) = 1 Res(f,0) = (((8−0)/(4−0))) = 2 ∫_C f(z) dz = 2iπΣInd_C (z_k )Res(f,z_k ) ∫_C f(z) dz = 2iπ(−1−2) = −6iπ

$$\left(\mathrm{A}\right) \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{8}−{z}}{{z}\left(\mathrm{4}−{z}\right)} \\ $$$$\mathrm{Res}\left({f},−\mathrm{4}\right)\:=\:\mathrm{2}\left(\frac{\mathrm{8}−\mathrm{4}}{\mathrm{4}}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{Res}\left({f},\mathrm{0}\right)\:=\:\left(\frac{\mathrm{8}−\mathrm{0}}{\mathrm{4}−\mathrm{0}}\right)\:=\:\mathrm{2} \\ $$$$\int_{\mathrm{C}} {f}\left({z}\right)\:{dz}\:=\:\mathrm{2}{i}\pi\Sigma\mathrm{Ind}_{\mathrm{C}} \left({z}_{{k}} \right)\mathrm{Res}\left({f},{z}_{{k}} \right) \\ $$$$\int_{\mathrm{C}} {f}\left({z}\right)\:{dz}\:=\:\mathrm{2}{i}\pi\left(−\mathrm{1}−\mathrm{2}\right)\:=\:−\mathrm{6}{i}\pi \\ $$

Answered by mathmax by abdo last updated on 26/Jul/21

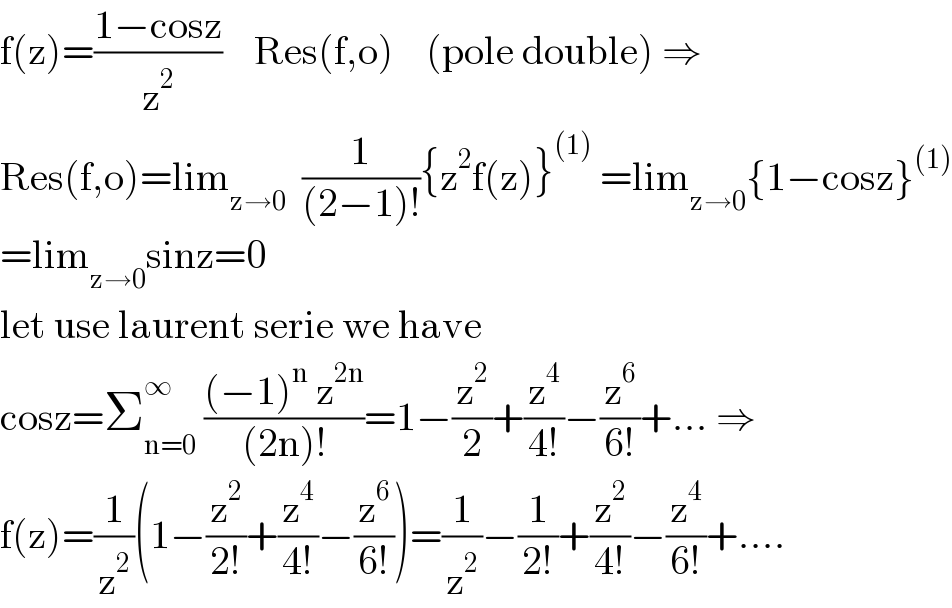
f(z)=((1−cosz)/z^2 ) Res(f,o) (pole double) ⇒ Res(f,o)=lim_(z→0) (1/((2−1)!)){z^2 f(z)}^((1)) =lim_(z→0) {1−cosz}^((1)) =lim_(z→0) sinz=0 let use laurent serie we have cosz=Σ_(n=0) ^∞ (((−1)^n z^(2n) )/((2n)!))=1−(z^2 /2)+(z^4 /(4!))−(z^6 /(6!))+... ⇒ f(z)=(1/z^2 )(1−(z^2 /(2!))+(z^4 /(4!))−(z^6 /(6!)))=(1/z^2 )−(1/(2!))+(z^2 /(4!))−(z^4 /(6!))+....

$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}−\mathrm{cosz}}{\mathrm{z}^{\mathrm{2}} }\:\:\:\:\mathrm{Res}\left(\mathrm{f},\mathrm{o}\right)\:\:\:\:\left(\mathrm{pole}\:\mathrm{double}\right)\:\Rightarrow \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{o}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\mathrm{z}^{\mathrm{2}} \mathrm{f}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \left\{\mathrm{1}−\mathrm{cosz}\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \mathrm{sinz}=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{use}\:\mathrm{laurent}\:\mathrm{serie}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{cosz}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}=\mathrm{1}−\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{z}^{\mathrm{4}} }{\mathrm{4}!}−\frac{\mathrm{z}^{\mathrm{6}} }{\mathrm{6}!}+...\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{z}^{\mathrm{4}} }{\mathrm{4}!}−\frac{\mathrm{z}^{\mathrm{6}} }{\mathrm{6}!}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{4}!}−\frac{\mathrm{z}^{\mathrm{4}} }{\mathrm{6}!}+.... \\ $$

Commented by mathmax by abdo last updated on 26/Jul/21

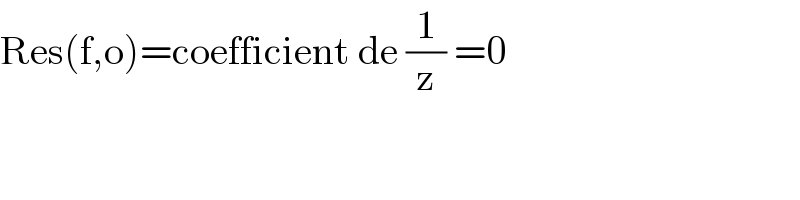
Res(f,o)=coefficient de (1/z) =0

$$\mathrm{Res}\left(\mathrm{f},\mathrm{o}\right)=\mathrm{coefficient}\:\mathrm{de}\:\frac{\mathrm{1}}{\mathrm{z}}\:=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com