Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 148302 by mathmax by abdo last updated on 26/Jul/21

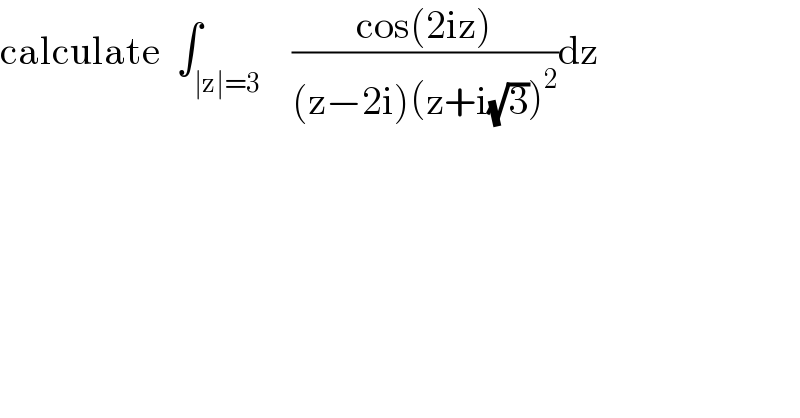
calculate ∫_(∣z∣=3) ((cos(2iz))/((z−2i)(z+i(√3))^2 ))dz

$$\mathrm{calculate}\:\:\int_{\mid\mathrm{z}\mid=\mathrm{3}} \:\:\:\frac{\mathrm{cos}\left(\mathrm{2iz}\right)}{\left(\mathrm{z}−\mathrm{2i}\right)\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{dz} \\ $$

Answered by Olaf_Thorendsen last updated on 27/Jul/21

f(z) = ((cos(2iz))/((z−2i)(z+i(√3))^2 )) Res(f,2i) = lim_(z→2i) ((cos(2iz))/((z+i(√3))^2 )) Res(f,2i) = ((cos(4))/((2i+i(√3))^2 )) Res(f,2i) = ((cos(4))/(−7−4(√3))) Res(f,2i) = −cos(4)(7−4(√3)) Res(f,−i(√3)) = lim_(z→−i(√3)) (∂/∂z).((cos(2iz))/(z−2i)) Res(f,−i(√3)) = lim_(z→−i(√3)) ((−2isin(2iz)(z−2i)−cos(2iz))/((z−2i)^2 )) Res(f,−i(√3)) = ((2(2+(√3))sin(2(√3))−cos(2(√3)))/(−7−4(√3))) Res(f,−i(√3)) = −[2(2+(√3))sin(2(√3))−cos(2(√3))(7−4(√3)) Res(f,−i(√3)) = (7−4(√3))cos(2(√3))−2(2−(√3))sin(2(√3)) Ω = ∫_(∣z∣=3) f(z) dz Ω = 2iπ(Res(f,2i)+Res(f,−i(√3))) Ω = 2iπ[(7−4(√3))(cos(2(√3))−cos(4)) −2(2−(√3))sin(2(√3))]

$${f}\left({z}\right)\:=\:\frac{\mathrm{cos}\left(\mathrm{2}{iz}\right)}{\left({z}−\mathrm{2}{i}\right)\left({z}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left({f},\mathrm{2}{i}\right)\:=\:\underset{{z}\rightarrow\mathrm{2}{i}} {\mathrm{lim}}\:\frac{\mathrm{cos}\left(\mathrm{2}{iz}\right)}{\left({z}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left({f},\mathrm{2}{i}\right)\:=\:\frac{\mathrm{cos}\left(\mathrm{4}\right)}{\left(\mathrm{2}{i}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left({f},\mathrm{2}{i}\right)\:=\:\frac{\mathrm{cos}\left(\mathrm{4}\right)}{−\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Res}\left({f},\mathrm{2}{i}\right)\:=\:−\mathrm{cos}\left(\mathrm{4}\right)\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right) \\ $$$$ \\ $$$$\mathrm{Res}\left({f},−{i}\sqrt{\mathrm{3}}\right)\:=\:\underset{{z}\rightarrow−{i}\sqrt{\mathrm{3}}} {\mathrm{lim}}\:\frac{\partial}{\partial{z}}.\frac{\mathrm{cos}\left(\mathrm{2}{iz}\right)}{{z}−\mathrm{2}{i}} \\ $$$$\mathrm{Res}\left({f},−{i}\sqrt{\mathrm{3}}\right)\:=\:\underset{{z}\rightarrow−{i}\sqrt{\mathrm{3}}} {\mathrm{lim}}\:\frac{−\mathrm{2}{i}\mathrm{sin}\left(\mathrm{2}{iz}\right)\left({z}−\mathrm{2}{i}\right)−\mathrm{cos}\left(\mathrm{2}{iz}\right)}{\left({z}−\mathrm{2}{i}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Res}\left({f},−{i}\sqrt{\mathrm{3}}\right)\:=\:\frac{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)−\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)}{−\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Res}\left({f},−{i}\sqrt{\mathrm{3}}\right)\:=\:−\left[\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)−\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)\right. \\ $$$$\mathrm{Res}\left({f},−{i}\sqrt{\mathrm{3}}\right)\:=\:\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)−\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right) \\ $$$$ \\ $$$$\Omega\:=\:\int_{\mid{z}\mid=\mathrm{3}} {f}\left({z}\right)\:{dz} \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi\left(\mathrm{Res}\left({f},\mathrm{2}{i}\right)+\mathrm{Res}\left({f},−{i}\sqrt{\mathrm{3}}\right)\right) \\ $$$$ \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi\left[\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)\left(\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)−\mathrm{cos}\left(\mathrm{4}\right)\right)\right. \\ $$$$\left.−\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\right] \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 27/Jul/21

thank sir

$$\mathrm{thank}\:\mathrm{sir} \\ $$

Answered by mathmax by abdo last updated on 27/Jul/21

Ψ=∫_(∣z∣=3) ((cos(2iz))/((z−2i)(z+i(√3))^2 ))dx and ϕ(z)=((cos(2iz))/((z−2i)(z+i(√3))^2 )) les poles de ϕ sont 2i(simple) et −i(√3)(double) en appliquant le theoreme des residus on obtient ∫_(∣z∣=3) ϕ(z)dz=2iπ {Res(ϕ,2i)+Res(ϕ,−i(√3))} Res(ϕ,2i)=lim_(z→2i) (z−2i)ϕ(z)=lim_(z→2i) ((cos(2iz))/((z+i(√3))^2 )) =((cos(4))/((2i+i(√3))^2 ))=−((cos4)/((2+(√3))^2 ))=−((cos4)/(4+4(√3)+3))=−((cos4)/(7+4(√3))) Res(ϕ,−i(√3)) =lim_(z→−i(√3)) (1/((2−1)!)){(z−i(√3))ϕ(z)}^((1)) =lim_(z→−i(√3)) {((cos(2iz))/(z−2i))}^((1)) =lim_(z→−i(√3)) {((−2isin(2iz)(z−2i)−cos(2iz))/((z−2i)^2 ))} =((−2isin(2i(−i(√3))(−i(√3)−2i)−cos(2i(−i(√3))))/((−i(√3)−2i)^2 )) =((−2sin(2(√3))(2+(√3))−cos(2(√3)))/(−(2+(√3))^2 )) =(((4+2(√3))sin(2(√3))+cos(2(√3)))/(7+4(√3))) ⇒ ∫_C ϕ(z)dz=2iπ{−((cos4)/(7+4(√3)))+(((4+2(√3))sin(2(√3))+cos(2(√3)))/(7+4(√3)))} =((2iπ)/(7+4(√3)))(−cos4+(4+2(√3))sin(2(√3))+cos(2(√3)))=Ψ

$$\Psi=\int_{\mid\mathrm{z}\mid=\mathrm{3}} \:\:\frac{\mathrm{cos}\left(\mathrm{2iz}\right)}{\left(\mathrm{z}−\mathrm{2i}\right)\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{and}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{cos}\left(\mathrm{2iz}\right)}{\left(\mathrm{z}−\mathrm{2i}\right)\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{les}\:\mathrm{poles}\:\mathrm{de}\:\varphi\:\mathrm{sont}\:\mathrm{2i}\left(\mathrm{simple}\right)\:\:\mathrm{et}\:−\mathrm{i}\sqrt{\mathrm{3}}\left(\mathrm{double}\right) \\ $$$$\mathrm{en}\:\mathrm{appliquant}\:\mathrm{le}\:\mathrm{theoreme}\:\mathrm{des}\:\mathrm{residus}\:\:\mathrm{on}\:\mathrm{obtient} \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{3}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\:\left\{\mathrm{Res}\left(\varphi,\mathrm{2i}\right)+\mathrm{Res}\left(\varphi,−\mathrm{i}\sqrt{\mathrm{3}}\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{2i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2i}} \left(\mathrm{z}−\mathrm{2i}\right)\varphi\left(\mathrm{z}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2i}} \:\:\frac{\mathrm{cos}\left(\mathrm{2iz}\right)}{\left(\mathrm{z}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{cos}\left(\mathrm{4}\right)}{\left(\mathrm{2i}+\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=−\frac{\mathrm{cos4}}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=−\frac{\mathrm{cos4}}{\mathrm{4}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{3}}=−\frac{\mathrm{cos4}}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Res}\left(\varphi,−\mathrm{i}\sqrt{\mathrm{3}}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\sqrt{\mathrm{3}}\right)\varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:\left\{\frac{\mathrm{cos}\left(\mathrm{2iz}\right)}{\mathrm{z}−\mathrm{2i}}\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{i}\sqrt{\mathrm{3}}} \:\:\:\left\{\frac{−\mathrm{2isin}\left(\mathrm{2iz}\right)\left(\mathrm{z}−\mathrm{2i}\right)−\mathrm{cos}\left(\mathrm{2iz}\right)}{\left(\mathrm{z}−\mathrm{2i}\right)^{\mathrm{2}} }\right\} \\ $$$$=\frac{−\mathrm{2isin}\left(\mathrm{2i}\left(−\mathrm{i}\sqrt{\mathrm{3}}\right)\left(−\mathrm{i}\sqrt{\mathrm{3}}−\mathrm{2i}\right)−\mathrm{cos}\left(\mathrm{2i}\left(−\mathrm{i}\sqrt{\mathrm{3}}\right)\right)\right.}{\left(−\mathrm{i}\sqrt{\mathrm{3}}−\mathrm{2i}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)−\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)}{−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)+\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{\mathrm{C}} \varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\left\{−\frac{\mathrm{cos4}}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}}+\frac{\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)+\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}}\right\} \\ $$$$=\frac{\mathrm{2i}\pi}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}}\left(−\mathrm{cos4}+\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)+\mathrm{cos}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\right)=\Psi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com