
Question and Answers Forum
Question Number 148408 by cesarL last updated on 27/Jul/21
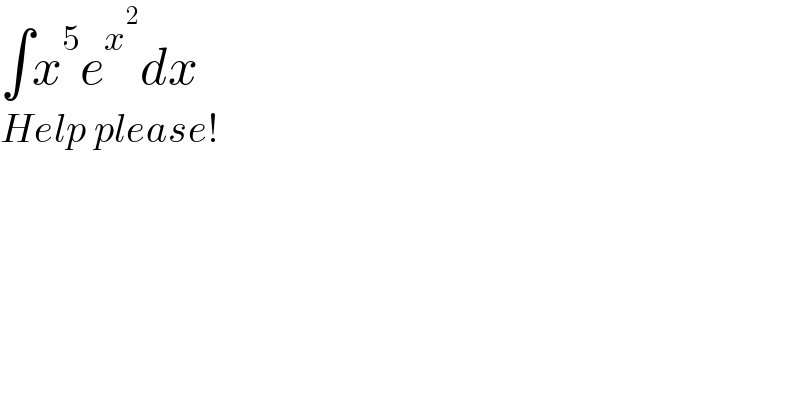
Answered by Olaf_Thorendsen last updated on 27/Jul/21
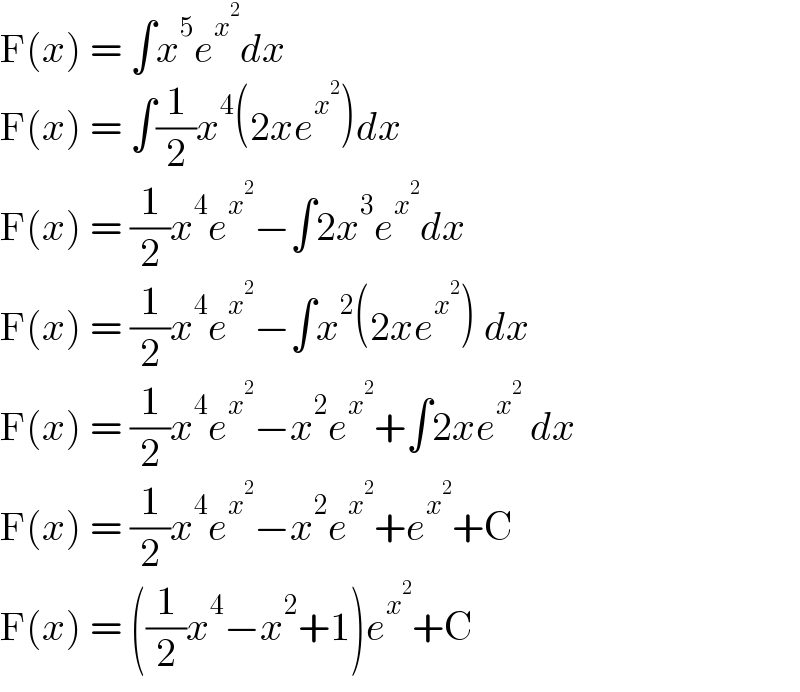
Commented by cesarL last updated on 27/Jul/21

Answered by Math_Freak last updated on 27/Jul/21

| ||
Question and Answers Forum | ||
Question Number 148408 by cesarL last updated on 27/Jul/21 | ||
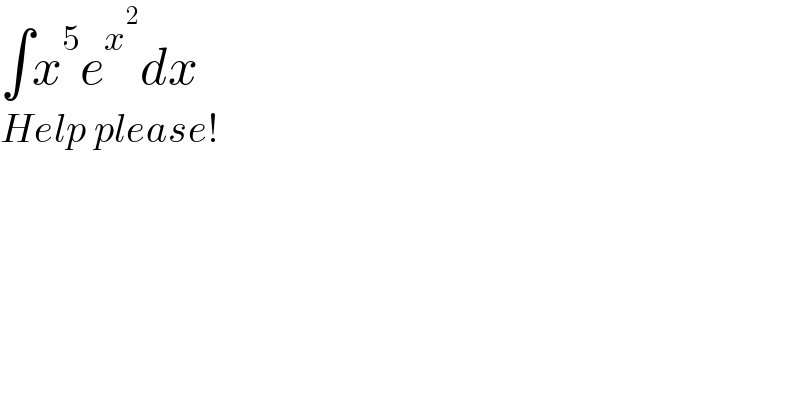 | ||
Answered by Olaf_Thorendsen last updated on 27/Jul/21 | ||
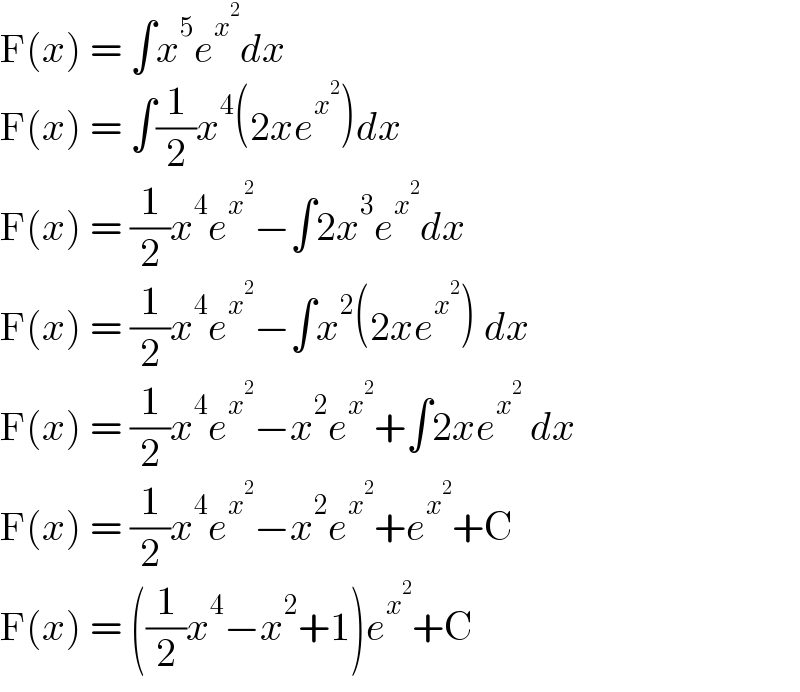 | ||
| ||
Commented by cesarL last updated on 27/Jul/21 | ||
 | ||
Answered by Math_Freak last updated on 27/Jul/21 | ||
 | ||
| ||