
Question and Answers Forum
Question Number 148427 by Rustambek last updated on 27/Jul/21

Answered by Ar Brandon last updated on 27/Jul/21
=2+Σ_(k=2) ^(2020) [(k+1)!−k!] =2+[(3!−2!)+(4!−3!)+∙∙∙(2021!−2020!)] =2021!](Q148429.png)
Commented by Rustambek last updated on 27/Jul/21

Answered by Olaf_Thorendsen last updated on 27/Jul/21
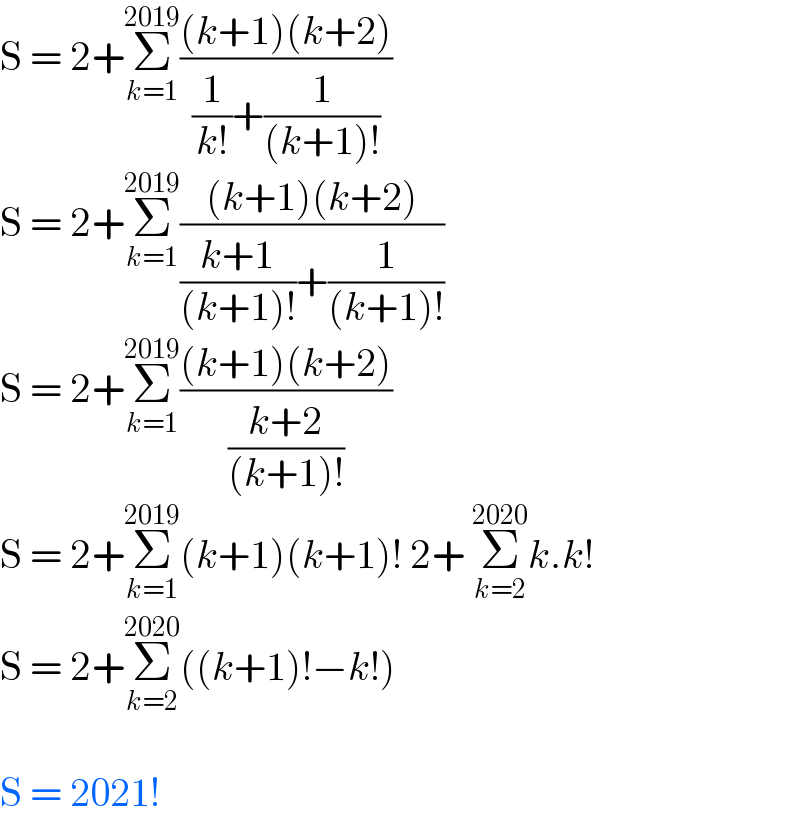
| ||
Question and Answers Forum | ||
Question Number 148427 by Rustambek last updated on 27/Jul/21 | ||
 | ||
Answered by Ar Brandon last updated on 27/Jul/21 | ||
=2+Σ_(k=2) ^(2020) [(k+1)!−k!] =2+[(3!−2!)+(4!−3!)+∙∙∙(2021!−2020!)] =2021!](Q148429.png) | ||
| ||
Commented by Rustambek last updated on 27/Jul/21 | ||
 | ||
Answered by Olaf_Thorendsen last updated on 27/Jul/21 | ||
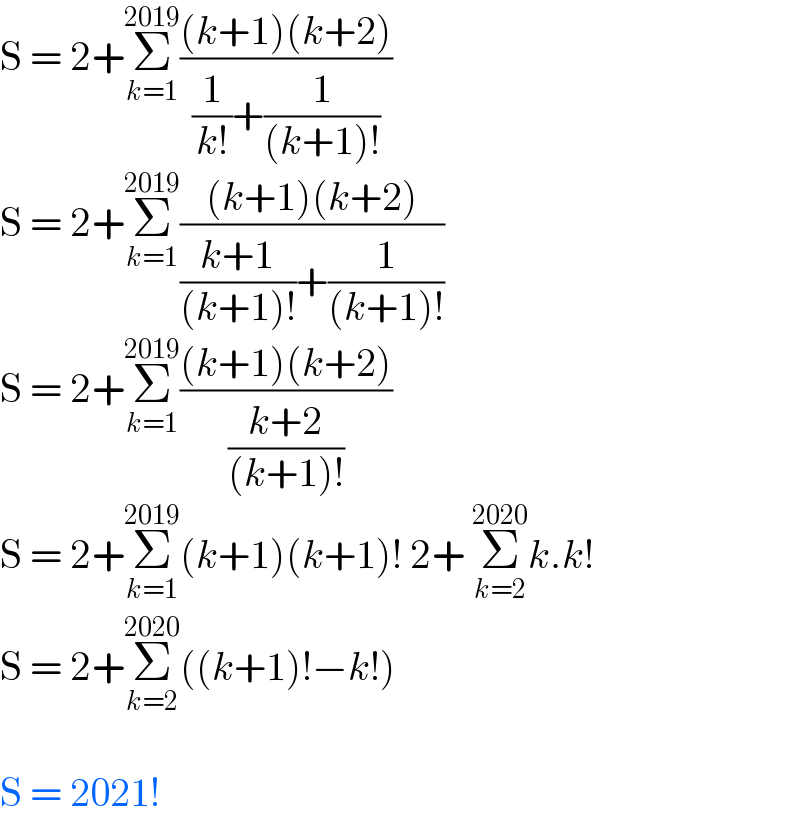 | ||
| ||