
Question and Answers Forum
Question Number 148467 by bramlexs22 last updated on 28/Jul/21
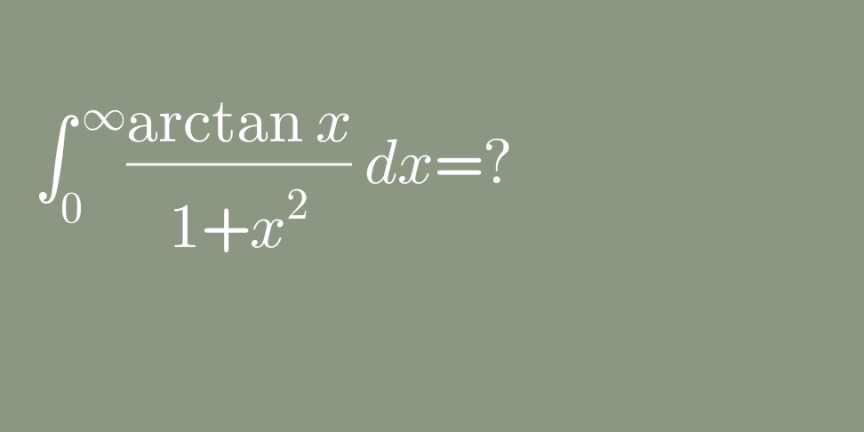
Answered by puissant last updated on 28/Jul/21
![x=tan(t)⇒dx=1+tan^2 (t)dt 0≤x≤∞ ⇒ 0≤t≤(π/2) ⇒I=∫_0 ^(π/2) ((arctan(tan(t)))/(1+tan^2 (t)))(1+tan^2 (t))dt =∫_0 ^(π/2) tdt = (1/2)[t^2 ]_0 ^(π/2) = (1/2)×(π^2 /4)=(π^2 /8) ⇒I = (π^2 /8)....Trivial.](Q148471.png)
Answered by Ar Brandon last updated on 28/Jul/21
![I=∫_0 ^∞ ((arctanx)/(1+x^2 ))dx =∫_0 ^(π/2) udu=[(u^2 /2)]_0 ^(π/2) =(π^2 /8)](Q148484.png)
Commented by Ar Brandon last updated on 28/Jul/21
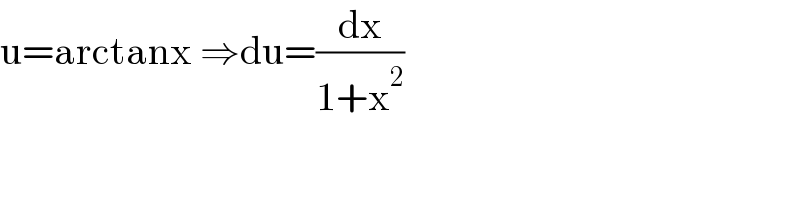
| ||
Question and Answers Forum | ||
Question Number 148467 by bramlexs22 last updated on 28/Jul/21 | ||
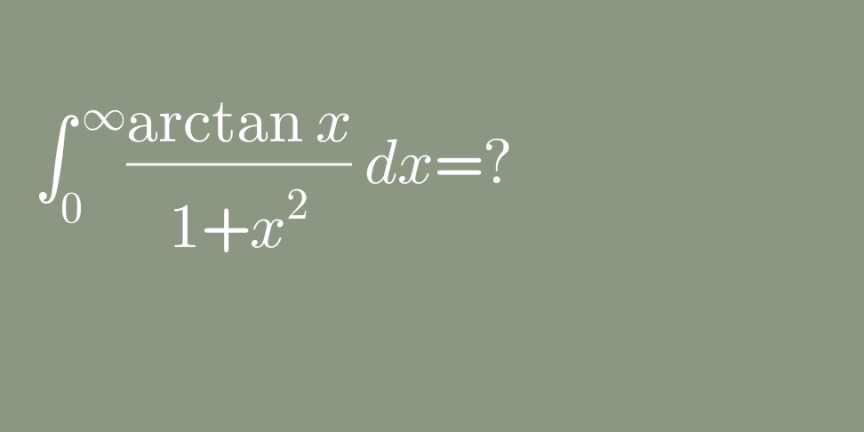 | ||
Answered by puissant last updated on 28/Jul/21 | ||
![x=tan(t)⇒dx=1+tan^2 (t)dt 0≤x≤∞ ⇒ 0≤t≤(π/2) ⇒I=∫_0 ^(π/2) ((arctan(tan(t)))/(1+tan^2 (t)))(1+tan^2 (t))dt =∫_0 ^(π/2) tdt = (1/2)[t^2 ]_0 ^(π/2) = (1/2)×(π^2 /4)=(π^2 /8) ⇒I = (π^2 /8)....Trivial.](Q148471.png) | ||
| ||
Answered by Ar Brandon last updated on 28/Jul/21 | ||
![I=∫_0 ^∞ ((arctanx)/(1+x^2 ))dx =∫_0 ^(π/2) udu=[(u^2 /2)]_0 ^(π/2) =(π^2 /8)](Q148484.png) | ||
| ||
Commented by Ar Brandon last updated on 28/Jul/21 | ||
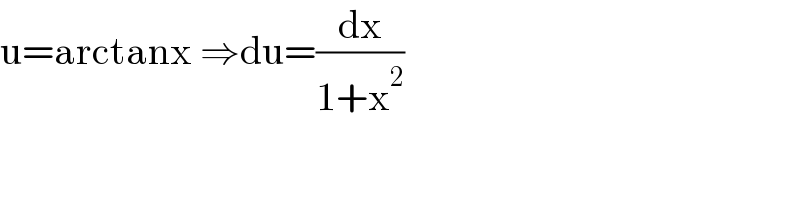 | ||