
Question and Answers Forum
Question Number 148565 by mathmax by abdo last updated on 29/Jul/21
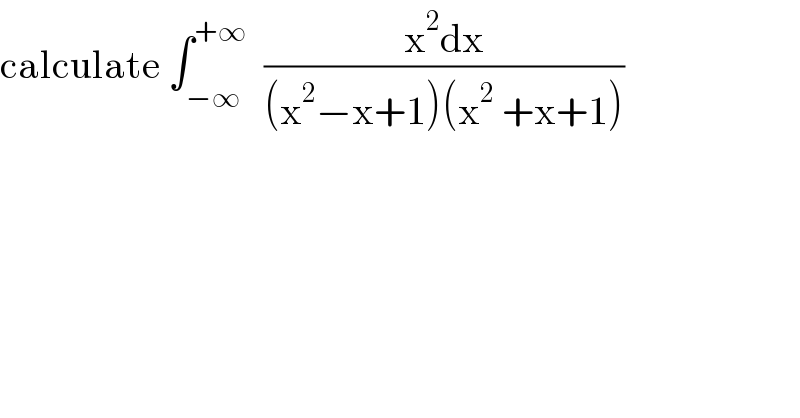
Answered by Ar Brandon last updated on 29/Jul/21
![Υ=∫_(−∞) ^(+∞) ((x^2 dx)/((x^2 −x+1)(x^2 +x+1)))=2∫_0 ^∞ ((x^2 dx)/((x^2 −x+1)(x^2 +x+1))) =2∫_0 ^1 ((x^2 dx)/((x^2 −x+1)(x^2 +x+1)))+2∫_1 ^∞ ((x^2 dx)/((x^2 −x+1)(x^2 +x+1))) =2∫_0 ^1 ((x^2 dx)/((x^2 −x+1)(x^2 +x+1)))+2∫_0 ^1 (dx/((x^2 −x+1)(x^2 +x+1))) =2∫_0 ^1 ((x^2 +1)/((x^2 −x+1)(x^2 +x+1)))dx=2∫_0 ^1 ((x^2 +1)/(x^4 +x^2 +1))dx =2∫_0 ^1 ((1+(1/x^2 ))/(x^2 +1+(1/x^2 )))dx=2∫_0 ^1 ((1+(1/x^2 ))/((x−(1/x))^2 +3))dx =2∫_0 ^1 ((d(x−(1/x)))/((x−(1/x))^2 +3))=(2/( (√3)))[arctan(((x^2 −1)/( (√3)x)))]_0 ^1 =(π/( (√3)))](Q148605.png)
Answered by mathmax by abdo last updated on 29/Jul/21

| ||
Question and Answers Forum | ||
Question Number 148565 by mathmax by abdo last updated on 29/Jul/21 | ||
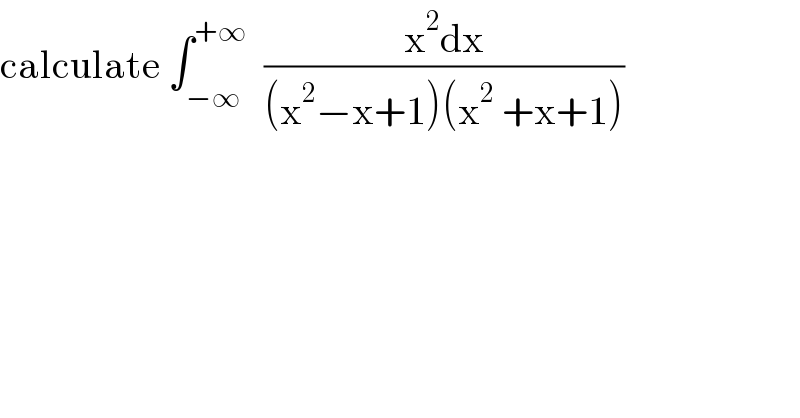 | ||
Answered by Ar Brandon last updated on 29/Jul/21 | ||
![Υ=∫_(−∞) ^(+∞) ((x^2 dx)/((x^2 −x+1)(x^2 +x+1)))=2∫_0 ^∞ ((x^2 dx)/((x^2 −x+1)(x^2 +x+1))) =2∫_0 ^1 ((x^2 dx)/((x^2 −x+1)(x^2 +x+1)))+2∫_1 ^∞ ((x^2 dx)/((x^2 −x+1)(x^2 +x+1))) =2∫_0 ^1 ((x^2 dx)/((x^2 −x+1)(x^2 +x+1)))+2∫_0 ^1 (dx/((x^2 −x+1)(x^2 +x+1))) =2∫_0 ^1 ((x^2 +1)/((x^2 −x+1)(x^2 +x+1)))dx=2∫_0 ^1 ((x^2 +1)/(x^4 +x^2 +1))dx =2∫_0 ^1 ((1+(1/x^2 ))/(x^2 +1+(1/x^2 )))dx=2∫_0 ^1 ((1+(1/x^2 ))/((x−(1/x))^2 +3))dx =2∫_0 ^1 ((d(x−(1/x)))/((x−(1/x))^2 +3))=(2/( (√3)))[arctan(((x^2 −1)/( (√3)x)))]_0 ^1 =(π/( (√3)))](Q148605.png) | ||
| ||
Answered by mathmax by abdo last updated on 29/Jul/21 | ||
 | ||
| ||