
Question Number 148594 by mathdanisur last updated on 29/Jul/21
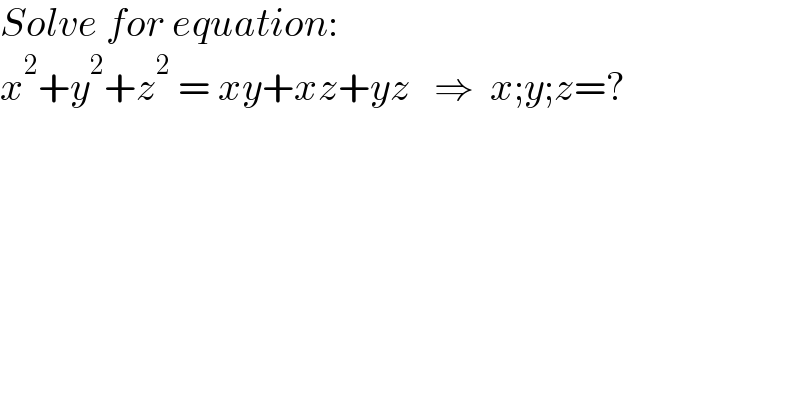
$${Solve}\:{for}\:{equation}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:=\:{xy}+{xz}+{yz}\:\:\:\Rightarrow\:\:{x};{y};{z}=? \\ $$
Commented by Rasheed.Sindhi last updated on 29/Jul/21
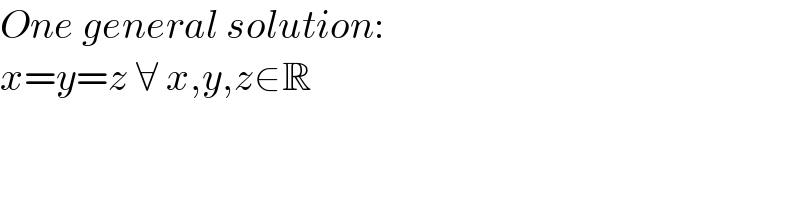
$${One}\:{general}\:{solution}: \\ $$$${x}={y}={z}\:\forall\:{x},{y},{z}\in\mathbb{R} \\ $$
Commented by mathdanisur last updated on 29/Jul/21
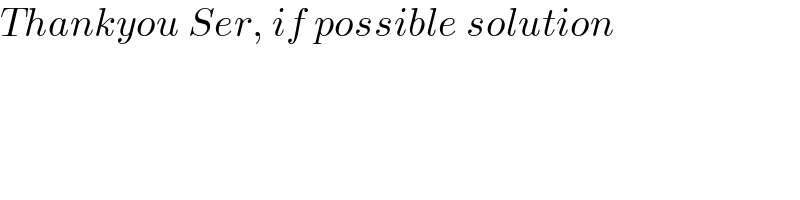
$${Thankyou}\:{Ser},\:{if}\:{possible}\:{solution} \\ $$
Answered by ajfour last updated on 29/Jul/21
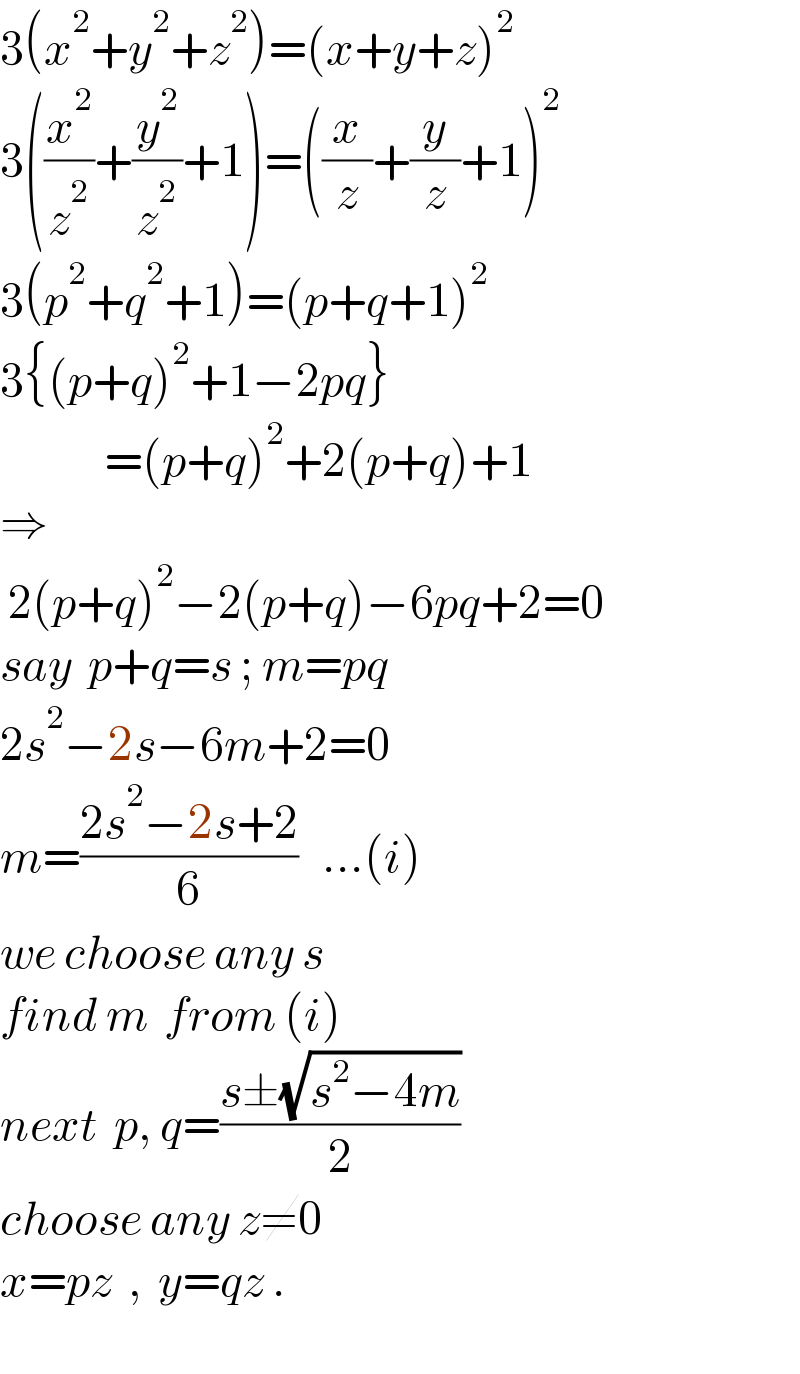
$$\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)=\left({x}+{y}+{z}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}\left(\frac{{x}^{\mathrm{2}} }{{z}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} }+\mathrm{1}\right)=\left(\frac{{x}}{{z}}+\frac{{y}}{{z}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{1}\right)=\left({p}+{q}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}\left\{\left({p}+{q}\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{pq}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({p}+{q}\right)^{\mathrm{2}} +\mathrm{2}\left({p}+{q}\right)+\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\:\mathrm{2}\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}\left({p}+{q}\right)−\mathrm{6}{pq}+\mathrm{2}=\mathrm{0} \\ $$$${say}\:\:{p}+{q}={s}\:;\:{m}={pq} \\ $$$$\mathrm{2}{s}^{\mathrm{2}} −\mathrm{2}{s}−\mathrm{6}{m}+\mathrm{2}=\mathrm{0} \\ $$$${m}=\frac{\mathrm{2}{s}^{\mathrm{2}} −\mathrm{2}{s}+\mathrm{2}}{\mathrm{6}}\:\:\:...\left({i}\right) \\ $$$${we}\:{choose}\:{any}\:{s} \\ $$$${find}\:{m}\:\:{from}\:\left({i}\right) \\ $$$${next}\:\:{p},\:{q}=\frac{{s}\pm\sqrt{{s}^{\mathrm{2}} −\mathrm{4}{m}}}{\mathrm{2}} \\ $$$${choose}\:{any}\:{z}\neq\mathrm{0} \\ $$$${x}={pz}\:\:,\:\:{y}={qz}\:. \\ $$$$ \\ $$
Commented by mathdanisur last updated on 29/Jul/21
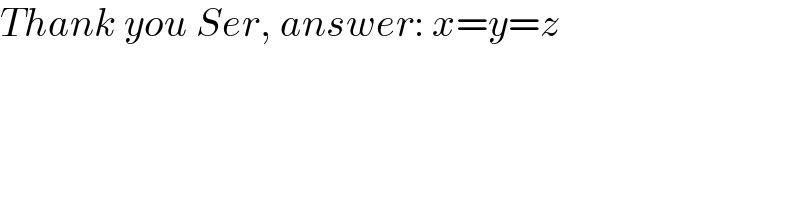
$${Thank}\:{you}\:{Ser},\:{answer}:\:{x}={y}={z} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Jul/21
![Assumed x,y,z∈R x^2 +y^2 +z^2 =xy+yz+zx x^2 −(y+z)x+y^2 −yz+z^2 =0 x=(((y+z)±(√((y+z)^2 −4(y^2 −yz+z^2 ))))/2) x=(((y+z)±(√(y^2 +2yz+z^2 −4y^2 +4yz−4z^2 )))/2) x=(((y+z)±(√(−3y^2 +6yz−3z^2 )))/2) x=(((y+z)±(√(−3(y^2 −2yz+z^2 ))))/2) x=(((y+z)±(√(−3(y−z)^2 )))/2) Since x∈R , (y−z)^2 =0 [(y−z)^2 >0⇒x∉R (y−z)^2 ≮0 ∵ y,z∈R ∴ (y−z)^2 =0 ] or y=z...........(i) x=((y+y)/2)=((2y)/2)=y.........(ii) From (i) & (ii): x=y=z](Q148665.png)
$${Assumed}\:{x},{y},{z}\in\mathbb{R} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={xy}+{yz}+{zx} \\ $$$${x}^{\mathrm{2}} −\left({y}+{z}\right){x}+{y}^{\mathrm{2}} −{yz}+{z}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{\left({y}+{z}\right)\pm\sqrt{\left({y}+{z}\right)^{\mathrm{2}} −\mathrm{4}\left({y}^{\mathrm{2}} −{yz}+{z}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$${x}=\frac{\left({y}+{z}\right)\pm\sqrt{{y}^{\mathrm{2}} +\mathrm{2}{yz}+{z}^{\mathrm{2}} −\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{yz}−\mathrm{4}{z}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${x}=\frac{\left({y}+{z}\right)\pm\sqrt{−\mathrm{3}{y}^{\mathrm{2}} +\mathrm{6}{yz}−\mathrm{3}{z}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${x}=\frac{\left({y}+{z}\right)\pm\sqrt{−\mathrm{3}\left({y}^{\mathrm{2}} −\mathrm{2}{yz}+{z}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$${x}=\frac{\left({y}+{z}\right)\pm\sqrt{−\mathrm{3}\left({y}−{z}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${Since}\:{x}\in\mathbb{R}\:,\:\left({y}−{z}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\left[\left({y}−{z}\right)^{\mathrm{2}} >\mathrm{0}\Rightarrow{x}\notin\mathbb{R}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\left({y}−{z}\right)^{\mathrm{2}} \nless\mathrm{0}\:\:\:\because\:{y},{z}\in\mathbb{R} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\left({y}−{z}\right)^{\mathrm{2}} =\mathrm{0}\:\right] \\ $$$$\:\:\:\:{or}\:\:\:{y}={z}...........\left({i}\right) \\ $$$${x}=\frac{{y}+{y}}{\mathrm{2}}=\frac{\mathrm{2}{y}}{\mathrm{2}}={y}.........\left({ii}\right) \\ $$$${From}\:\left({i}\right)\:\&\:\left({ii}\right): \\ $$$$\:\:\:\:\:{x}={y}={z} \\ $$
Commented by mathdanisur last updated on 30/Jul/21

$${Thank}\:{You}\:{Ser} \\ $$
