
Question and Answers Forum
Question Number 148609 by learner001 last updated on 29/Jul/21
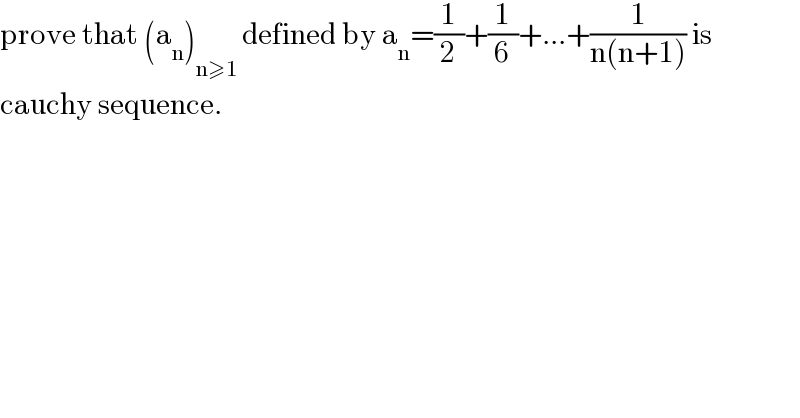
Commented by learner001 last updated on 29/Jul/21
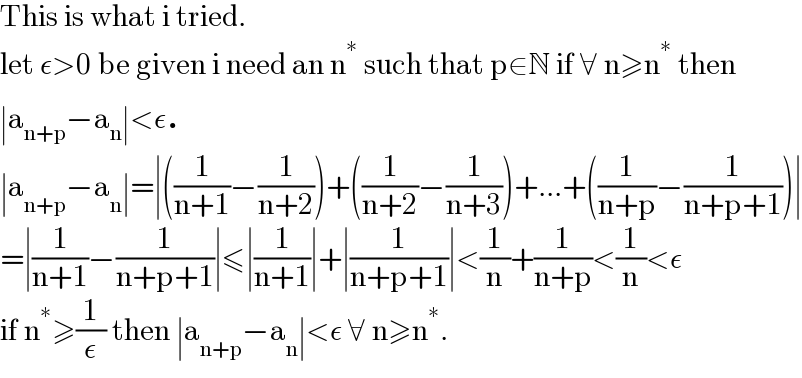
Commented by learner001 last updated on 29/Jul/21
is this correct?
| ||
Question and Answers Forum | ||
Question Number 148609 by learner001 last updated on 29/Jul/21 | ||
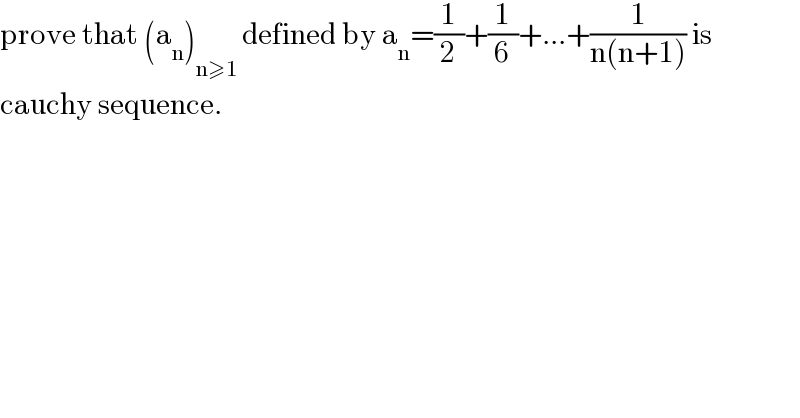 | ||
Commented by learner001 last updated on 29/Jul/21 | ||
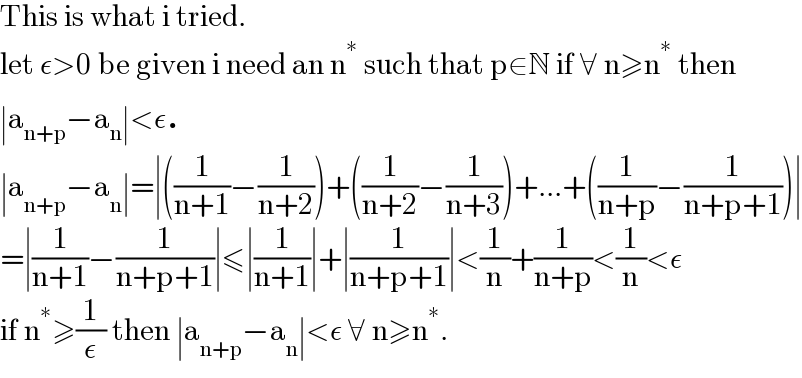 | ||
Commented by learner001 last updated on 29/Jul/21 | ||
is this correct? | ||