Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148645 by metamorfose last updated on 29/Jul/21

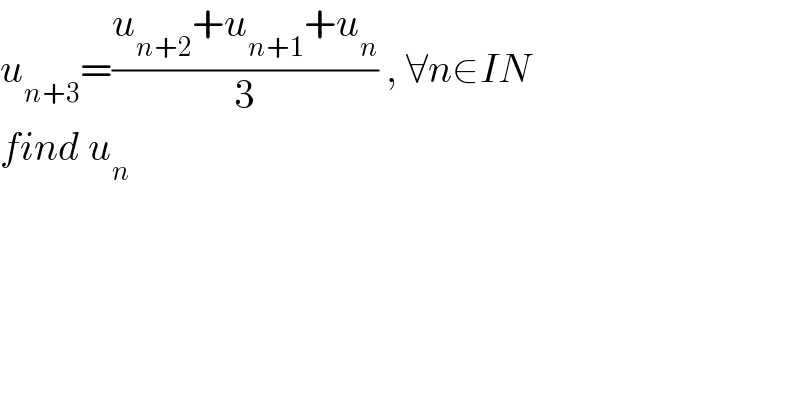
u_(n+3) =((u_(n+2) +u_(n+1) +u_n )/3) , ∀n∈IN find u_n

$${u}_{{n}+\mathrm{3}} =\frac{{u}_{{n}+\mathrm{2}} +{u}_{{n}+\mathrm{1}} +{u}_{{n}} }{\mathrm{3}}\:,\:\forall{n}\in{IN} \\ $$$${find}\:{u}_{{n}} \: \\ $$

Answered by Olaf_Thorendsen last updated on 29/Jul/21

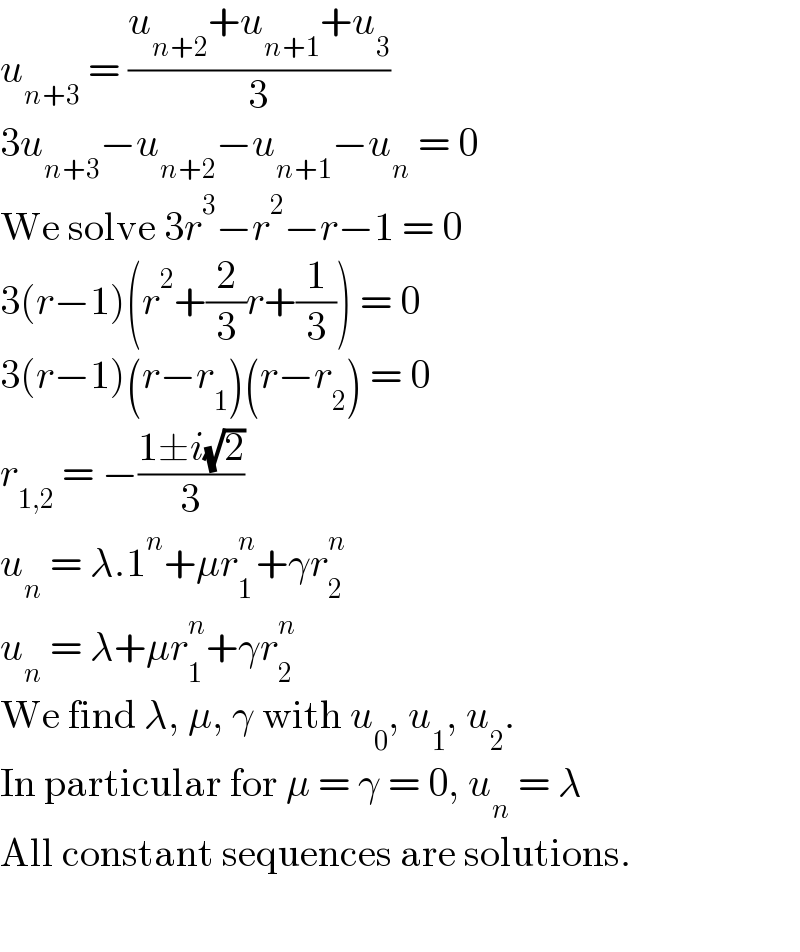
u_(n+3) = ((u_(n+2) +u_(n+1) +u_3 )/3) 3u_(n+3) −u_(n+2) −u_(n+1) −u_n = 0 We solve 3r^3 −r^2 −r−1 = 0 3(r−1)(r^2 +(2/3)r+(1/3)) = 0 3(r−1)(r−r_1 )(r−r_2 ) = 0 r_(1,2) = −((1±i(√2))/3) u_n = λ.1^n +μr_1 ^n +γr_2 ^n u_n = λ+μr_1 ^n +γr_2 ^n We find λ, μ, γ with u_0 , u_1 , u_2 . In particular for μ = γ = 0, u_n = λ All constant sequences are solutions.

$${u}_{{n}+\mathrm{3}} \:=\:\frac{{u}_{{n}+\mathrm{2}} +{u}_{{n}+\mathrm{1}} +{u}_{\mathrm{3}} }{\mathrm{3}} \\ $$$$\mathrm{3}{u}_{{n}+\mathrm{3}} −{u}_{{n}+\mathrm{2}} −{u}_{{n}+\mathrm{1}} −{u}_{{n}} \:=\:\mathrm{0} \\ $$$$\mathrm{We}\:\mathrm{solve}\:\mathrm{3}{r}^{\mathrm{3}} −{r}^{\mathrm{2}} −{r}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{3}\left({r}−\mathrm{1}\right)\left({r}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}{r}+\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{3}\left({r}−\mathrm{1}\right)\left({r}−{r}_{\mathrm{1}} \right)\left({r}−{r}_{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$${r}_{\mathrm{1},\mathrm{2}} \:=\:−\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${u}_{{n}} \:=\:\lambda.\mathrm{1}^{{n}} +\mu{r}_{\mathrm{1}} ^{{n}} +\gamma{r}_{\mathrm{2}} ^{{n}} \\ $$$${u}_{{n}} \:=\:\lambda+\mu{r}_{\mathrm{1}} ^{{n}} +\gamma{r}_{\mathrm{2}} ^{{n}} \\ $$$$\mathrm{We}\:\mathrm{find}\:\lambda,\:\mu,\:\gamma\:\mathrm{with}\:{u}_{\mathrm{0}} ,\:{u}_{\mathrm{1}} ,\:{u}_{\mathrm{2}} . \\ $$$$\mathrm{In}\:\mathrm{particular}\:\mathrm{for}\:\mu\:=\:\gamma\:=\:\mathrm{0},\:{u}_{{n}} \:=\:\lambda \\ $$$$\mathrm{All}\:\mathrm{constant}\:\mathrm{sequences}\:\mathrm{are}\:\mathrm{solutions}. \\ $$$$ \\ $$

Commented by Olaf_Thorendsen last updated on 29/Jul/21

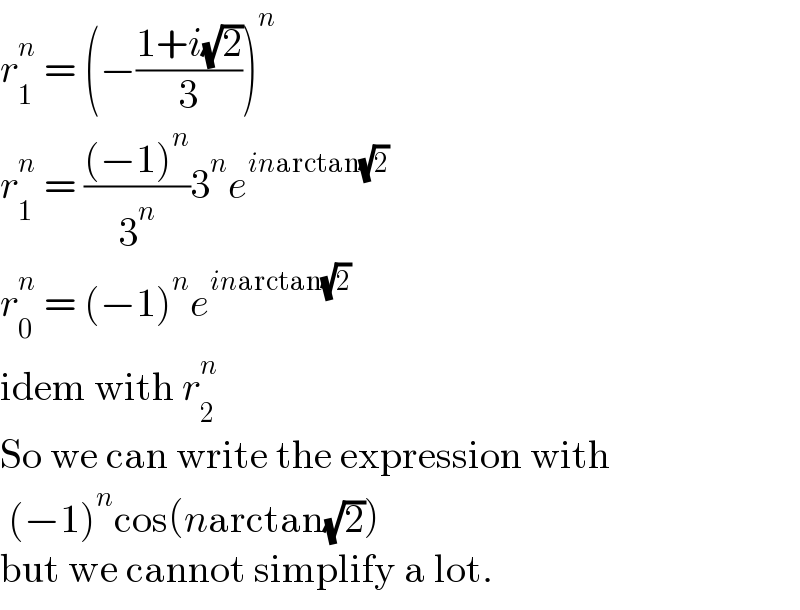
r_1 ^n = (−((1+i(√2))/3))^n r_1 ^n = (((−1)^n )/3^n )3^n e^(inarctan(√2)) r_0 ^n = (−1)^n e^(inarctan(√2)) idem with r_2 ^n So we can write the expression with (−1)^n cos(narctan(√2)) but we cannot simplify a lot.

$${r}_{\mathrm{1}} ^{{n}} \:=\:\left(−\frac{\mathrm{1}+{i}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{{n}} \\ $$$${r}_{\mathrm{1}} ^{{n}} \:=\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}^{{n}} }\mathrm{3}^{{n}} {e}^{{in}\mathrm{arctan}\sqrt{\mathrm{2}}} \\ $$$${r}_{\mathrm{0}} ^{{n}} \:=\:\left(−\mathrm{1}\right)^{{n}} {e}^{{in}\mathrm{arctan}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{idem}\:\mathrm{with}\:{r}_{\mathrm{2}} ^{{n}} \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{can}\:\mathrm{write}\:\mathrm{the}\:\mathrm{expression}\:\mathrm{with} \\ $$$$\:\left(−\mathrm{1}\right)^{{n}} \mathrm{cos}\left({n}\mathrm{arctan}\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{simplify}\:\mathrm{a}\:\mathrm{lot}. \\ $$

Commented by metamorfose last updated on 29/Jul/21

thank u sir.

$${thank}\:{u}\:{sir}. \\ $$

Commented by metamorfose last updated on 29/Jul/21

i thought the expression would be with cos

$${i}\:{thought}\:{the}\:{expression}\:{would}\:{be}\:{with}\:{cos} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com