Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 148655 by mathdanisur last updated on 29/Jul/21

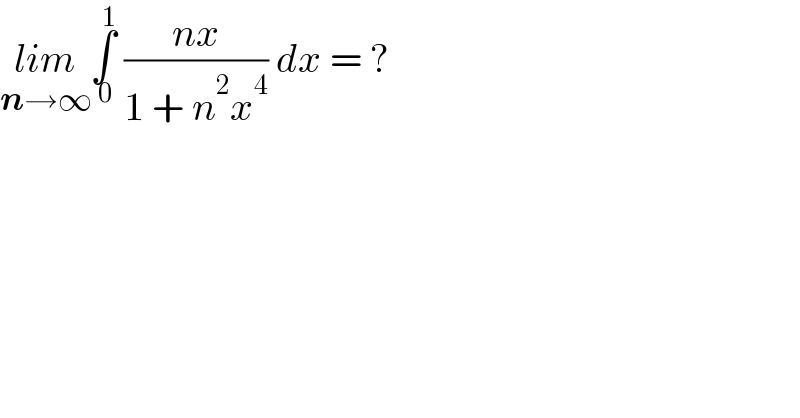
lim_(n→∞) ∫_( 0) ^( 1) ((nx)/(1 + n^2 x^4 )) dx = ?

$$\underset{\boldsymbol{{n}}\rightarrow\infty} {{lim}}\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{{nx}}{\mathrm{1}\:+\:{n}^{\mathrm{2}} {x}^{\mathrm{4}} }\:{dx}\:=\:? \\ $$

Answered by ArielVyny last updated on 29/Jul/21

n∫_0 ^1 (x/(1+(nx^2 )^2 ))dx=_(nx^2 =t) n∫_0 ^n ((√(t/n))/(1+t^2 )) n2xdx=dt→dx=(1/(2nx))dt=(1/(2n(√(t/n))))dt n∫_0 ^n ((√(t/n))/(1+t^2 ))×(1/(2n(√(t/n))))dt=(1/2)∫_0 ^n (1/(1+t^2 ))dt=(1/2)arctg(n) conclusion lim_(n→∞) ∫_0 ^1 ((nx)/(1+n^2 x^4 ))dx=(π/4)

$${n}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}+\left({nx}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=_{{nx}^{\mathrm{2}} ={t}} {n}\int_{\mathrm{0}} ^{{n}} \frac{\sqrt{\frac{{t}}{{n}}}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${n}\mathrm{2}{xdx}={dt}\rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{2}{nx}}{dt}=\frac{\mathrm{1}}{\mathrm{2}{n}\sqrt{\frac{{t}}{{n}}}}{dt} \\ $$$${n}\int_{\mathrm{0}} ^{{n}} \frac{\sqrt{\frac{{t}}{{n}}}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{2}{n}\sqrt{\frac{{t}}{{n}}}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{n}} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}{arctg}\left({n}\right) \\ $$$${conclusion}\:{li}\underset{{n}\rightarrow\infty} {{m}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{nx}}{\mathrm{1}+{n}^{\mathrm{2}} {x}^{\mathrm{4}} }{dx}=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$

Commented by mathdanisur last updated on 29/Jul/21

Thankyou Ser No solution or (π/4) .?

$${Thankyou}\:{Ser} \\ $$$${No}\:{solution}\:\:{or}\:\:\frac{\pi}{\mathrm{4}}\:.? \\ $$

Commented by ArielVyny last updated on 29/Jul/21

if you have any solutions you can post sir but i think the solution is (π/4)

$${if}\:{you}\:{have}\:{any}\:{solutions}\:{you}\:{can}\:{post}\:{sir} \\ $$$${but}\:{i}\:{think}\:{the}\:{solution}\:{is}\:\frac{\pi}{\mathrm{4}} \\ $$

Commented by mathdanisur last updated on 29/Jul/21

Thanks Ser

$${Thanks}\:{Ser} \\ $$

Answered by Ar Brandon last updated on 30/Jul/21

L=lim_(n→∞) ∫_0 ^1 ((nx)/(1+n^2 x^4 ))dx=(1/2)lim_(n→∞) ∫_0 ^1 ((2nx)/(1+(nx^2 )^2 ))dx =(1/2)lim_(n→∞) [arctan(nx^2 )]_0 ^1 =(1/2)[lim_(n→∞) arctan(n)−lim_(n→∞, x→0) arctan(nx^2 )] =(π/4)−(1/2)lim_(n→∞, x→0) arctan(nx^2 ) No solution L oscillates within 0≤L≤(π/4)

$$\mathscr{L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{nx}}{\mathrm{1}+{n}^{\mathrm{2}} {x}^{\mathrm{4}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{nx}}{\mathrm{1}+\left({nx}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{arctan}\left({nx}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{{n}\rightarrow\infty} {\mathrm{lim}arctan}\left({n}\right)−\underset{{n}\rightarrow\infty,\:{x}\rightarrow\mathrm{0}} {\mathrm{lim}arctan}\left({nx}^{\mathrm{2}} \right)\right] \\ $$$$\:\:\:\:\:=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty,\:{x}\rightarrow\mathrm{0}} {\mathrm{lim}arctan}\left({nx}^{\mathrm{2}} \right) \\ $$$$\mathrm{No}\:\mathrm{solution}\:\mathscr{L}\:\mathrm{oscillates}\:\mathrm{within}\:\mathrm{0}\leqslant\mathscr{L}\leqslant\frac{\pi}{\mathrm{4}} \\ $$

Commented by mathdanisur last updated on 29/Jul/21

Thank you Ser

$${Thank}\:{you}\:{Ser} \\ $$

Commented by mathmax by abdo last updated on 30/Jul/21

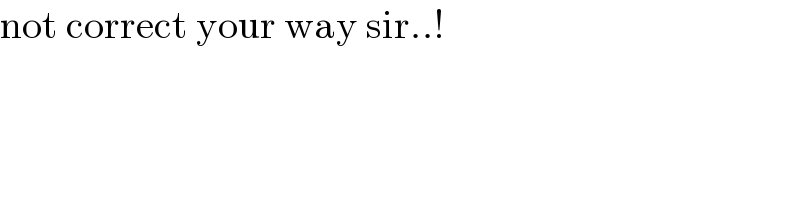
not correct your way sir..!

$$\mathrm{not}\:\mathrm{correct}\:\mathrm{your}\:\mathrm{way}\:\mathrm{sir}..! \\ $$

Commented by Ar Brandon last updated on 02/Aug/21

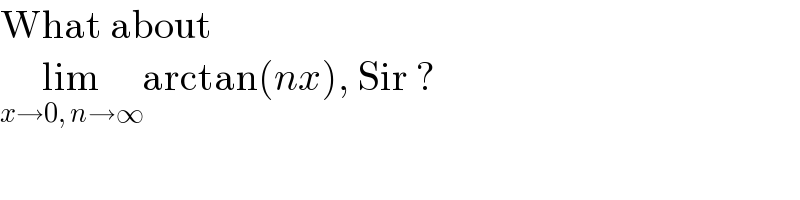
What about lim_(x→0, n→∞) arctan(nx), Sir ?

$$\mathrm{What}\:\mathrm{about} \\ $$$$\underset{{x}\rightarrow\mathrm{0},\:{n}\rightarrow\infty} {\mathrm{lim}arctan}\left({nx}\right),\:\mathrm{Sir}\:? \\ $$

Answered by mathmax by abdo last updated on 30/Jul/21

A_n =∫_0 ^1 ((nx)/(1+n^2 x^4 ))dx changement nx^2 =t give 2nxdx=dt ⇒ A_n =∫_0 ^n (dt/(2(1+t^2 ))) =(1/2)[arctant]_0 ^n =(1/2)arctan(n) ⇒ lim_(n→+∞) A_n =(1/2).(π/2)=(π/4)

$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{nx}}{\mathrm{1}+\mathrm{n}^{\mathrm{2}} \:\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\mathrm{changement}\:\mathrm{nx}^{\mathrm{2}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{2nxdx}=\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{arctant}\right]_{\mathrm{0}} ^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\left(\mathrm{n}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$

Commented by mathdanisur last updated on 31/Jul/21

Thank You Ser but answer: no solution

$${Thank}\:{You}\:{Ser} \\ $$$${but}\:{answer}:\:\:{no}\:{solution} \\ $$

Commented by mathmax by abdo last updated on 31/Jul/21

the answer is (π/4)sir

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\frac{\pi}{\mathrm{4}}\mathrm{sir} \\ $$

Commented by mathdanisur last updated on 01/Aug/21

Thankyou Sir

$${Thankyou}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com