
Question and Answers Forum
Question Number 148849 by EDWIN88 last updated on 31/Jul/21
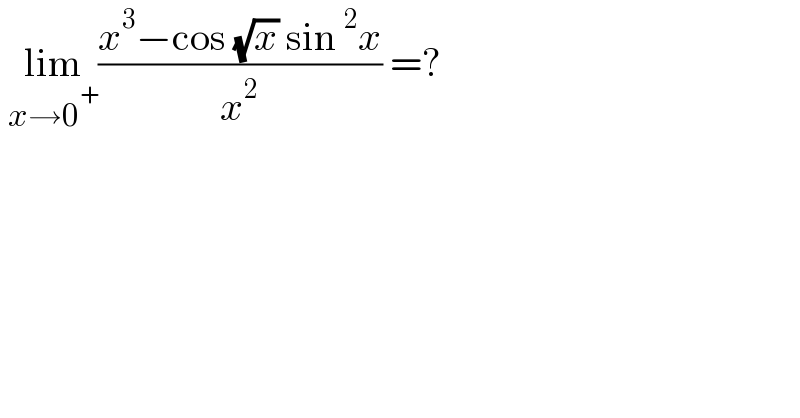
Answered by iloveisrael last updated on 01/Aug/21
![lim_(x→0^+ ) ((x^3 −sin^3 x+sin^3 x−cos (√x) sin^2 x)/x^2 ) =lim_(x→0^+ ) ((x^3 −sin^3 x)/x^2 )+lim_(x→0^+ ) ((sin^2 x(sin x−cos (√x)))/x^2 ) =lim_(x→0^+ ) (((x−sin x)(x^2 +x sin x+sin^2 x))/x^2 )+lim_(x→0^+ ) (sin x−cos (√x) ) =lim_(x→0^+ ) (((((x−sin x)/x^3 )). x^3 (x^2 +x sin x+sin^2 x))/x^2 )−1 =lim_(x→0) (((1/6)x^3 (x^2 +x sin x+sin^2 x))/x^2 )−1 =(1/6)[lim_(x→0^+ ) (x(x^2 +x sin x+sin^2 x)]−1= −1.](Q148870.png)
Answered by mathmax by abdo last updated on 01/Aug/21
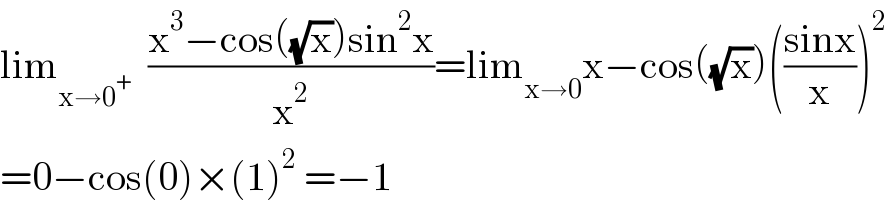
| ||
Question and Answers Forum | ||
Question Number 148849 by EDWIN88 last updated on 31/Jul/21 | ||
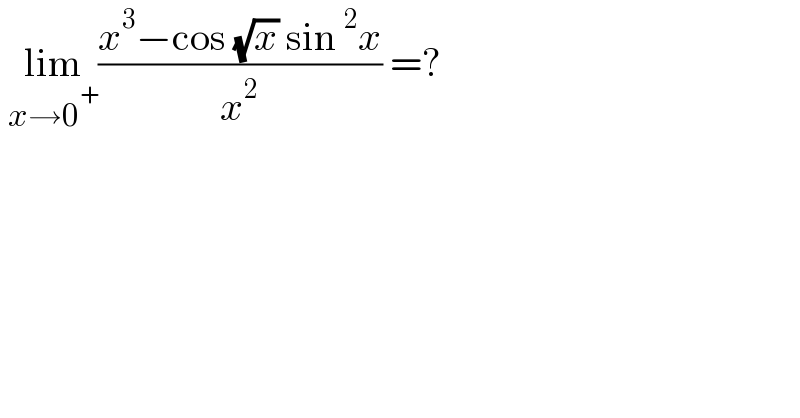 | ||
Answered by iloveisrael last updated on 01/Aug/21 | ||
![lim_(x→0^+ ) ((x^3 −sin^3 x+sin^3 x−cos (√x) sin^2 x)/x^2 ) =lim_(x→0^+ ) ((x^3 −sin^3 x)/x^2 )+lim_(x→0^+ ) ((sin^2 x(sin x−cos (√x)))/x^2 ) =lim_(x→0^+ ) (((x−sin x)(x^2 +x sin x+sin^2 x))/x^2 )+lim_(x→0^+ ) (sin x−cos (√x) ) =lim_(x→0^+ ) (((((x−sin x)/x^3 )). x^3 (x^2 +x sin x+sin^2 x))/x^2 )−1 =lim_(x→0) (((1/6)x^3 (x^2 +x sin x+sin^2 x))/x^2 )−1 =(1/6)[lim_(x→0^+ ) (x(x^2 +x sin x+sin^2 x)]−1= −1.](Q148870.png) | ||
| ||
Answered by mathmax by abdo last updated on 01/Aug/21 | ||
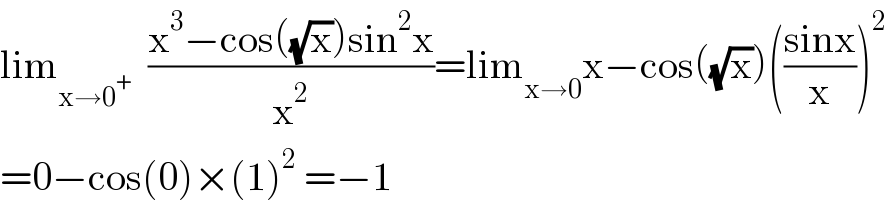 | ||
| ||