Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 149191 by mnjuly1970 last updated on 03/Aug/21

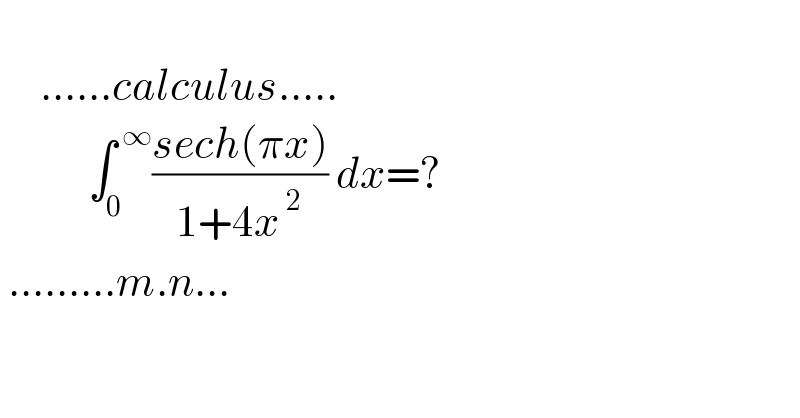
......calculus..... ∫_0 ^( ∞) ((sech(πx))/(1+4x^( 2) )) dx=? .........m.n...

$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:......{calculus}..... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sech}\left(\pi{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\:\mathrm{2}} }\:{dx}=? \\ $$$$\:.........{m}.{n}... \\ $$

Answered by mindispower last updated on 03/Aug/21

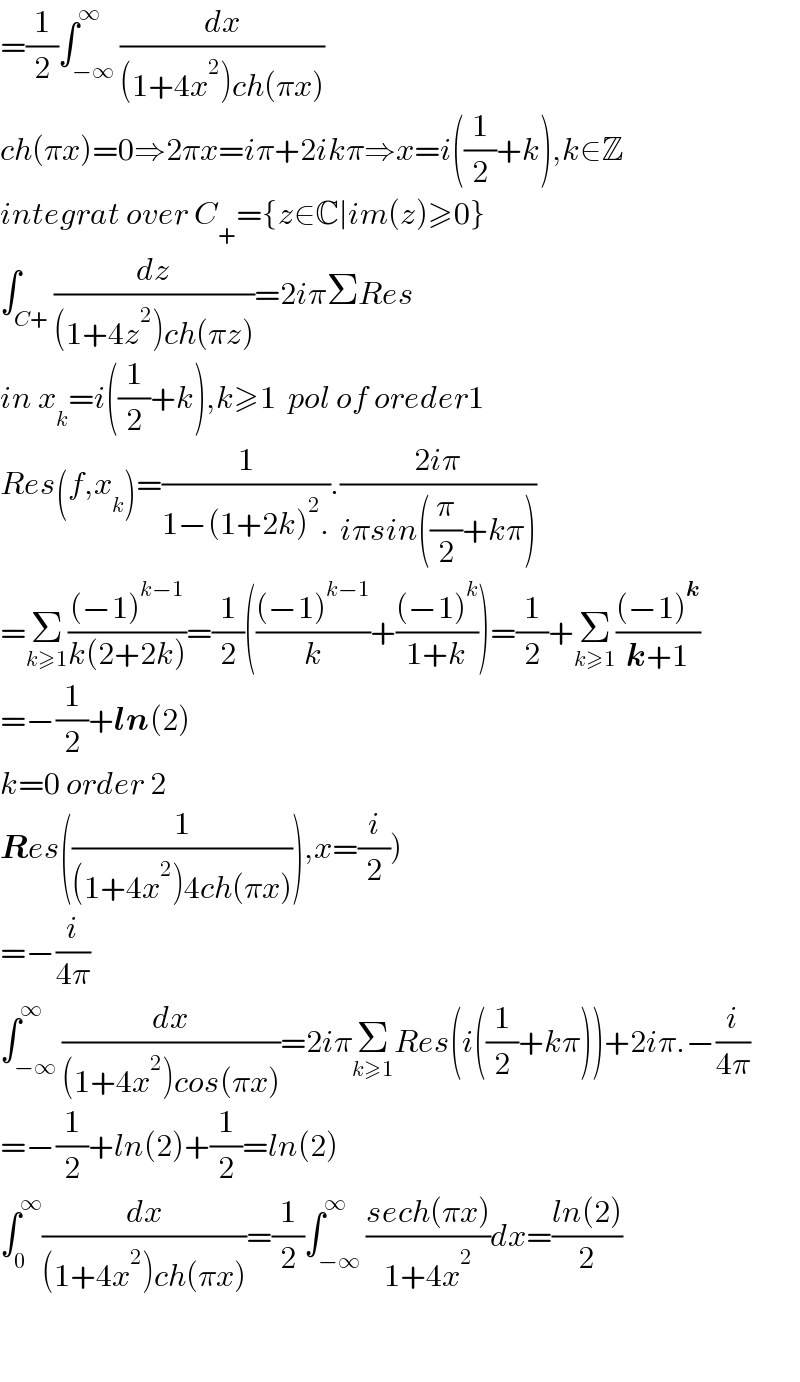
=(1/2)∫_(−∞) ^∞ (dx/((1+4x^2 )ch(πx))) ch(πx)=0⇒2πx=iπ+2ikπ⇒x=i((1/2)+k),k∈Z integrat over C_+ ={z∈C∣im(z)≥0} ∫_(C+) (dz/((1+4z^2 )ch(πz)))=2iπΣRes in x_k =i((1/2)+k),k≥1 pol of oreder1 Res(f,x_k )=(1/(1−(1+2k)^2 .)).((2iπ)/(iπsin((π/2)+kπ))) =Σ_(k≥1) (((−1)^(k−1) )/(k(2+2k)))=(1/2)((((−1)^(k−1) )/k)+(((−1)^k )/(1+k)))=(1/2)+Σ_(k≥1) (((−1)^k )/(k+1)) =−(1/2)+ln(2) k=0 order 2 Res((1/((1+4x^2 )4ch(πx)))),x=(i/2)) =−(i/(4π)) ∫_(−∞) ^∞ (dx/((1+4x^2 )cos(πx)))=2iπΣ_(k≥1) Res(i((1/2)+kπ))+2iπ.−(i/(4π)) =−(1/2)+ln(2)+(1/2)=ln(2) ∫_0 ^∞ (dx/((1+4x^2 )ch(πx)))=(1/2)∫_(−∞) ^∞ ((sech(πx))/(1+4x^2 ))dx=((ln(2))/2)

$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right){ch}\left(\pi{x}\right)} \\ $$$${ch}\left(\pi{x}\right)=\mathrm{0}\Rightarrow\mathrm{2}\pi{x}={i}\pi+\mathrm{2}{ik}\pi\Rightarrow{x}={i}\left(\frac{\mathrm{1}}{\mathrm{2}}+{k}\right),{k}\in\mathbb{Z} \\ $$$${integrat}\:{over}\:{C}_{+} =\left\{{z}\in\mathbb{C}\mid{im}\left({z}\right)\geqslant\mathrm{0}\right\} \\ $$$$\int_{{C}+} \frac{{dz}}{\left(\mathrm{1}+\mathrm{4}{z}^{\mathrm{2}} \right){ch}\left(\pi{z}\right)}=\mathrm{2}{i}\pi\Sigma{Res} \\ $$$${in}\:{x}_{{k}} ={i}\left(\frac{\mathrm{1}}{\mathrm{2}}+{k}\right),{k}\geqslant\mathrm{1}\:\:{pol}\:{of}\:{oreder}\mathrm{1} \\ $$$${Res}\left({f},{x}_{{k}} \right)=\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{1}+\mathrm{2}{k}\right)^{\mathrm{2}} .}.\frac{\mathrm{2}{i}\pi}{{i}\pi{sin}\left(\frac{\pi}{\mathrm{2}}+{k}\pi\right)} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}\left(\mathrm{2}+\mathrm{2}{k}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}+\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{1}+{k}}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{k}}} }{\boldsymbol{{k}}+\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}+\boldsymbol{{ln}}\left(\mathrm{2}\right) \\ $$$${k}=\mathrm{0}\:{order}\:\mathrm{2} \\ $$$$\left.\boldsymbol{{R}}{es}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)\mathrm{4}{ch}\left(\pi{x}\right)}\right),{x}=\frac{{i}}{\mathrm{2}}\right) \\ $$$$=−\frac{{i}}{\mathrm{4}\pi} \\ $$$$\int_{−\infty} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right){cos}\left(\pi{x}\right)}=\mathrm{2}{i}\pi\underset{{k}\geqslant\mathrm{1}} {\sum}{Res}\left({i}\left(\frac{\mathrm{1}}{\mathrm{2}}+{k}\pi\right)\right)+\mathrm{2}{i}\pi.−\frac{{i}}{\mathrm{4}\pi} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}+{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}={ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right){ch}\left(\pi{x}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{{sech}\left(\pi{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 06/Aug/21

thanks alot sir power..

$$\:\:\:\:{thanks}\:{alot}\:{sir}\:{power}.. \\ $$

Answered by Kamel last updated on 03/Aug/21

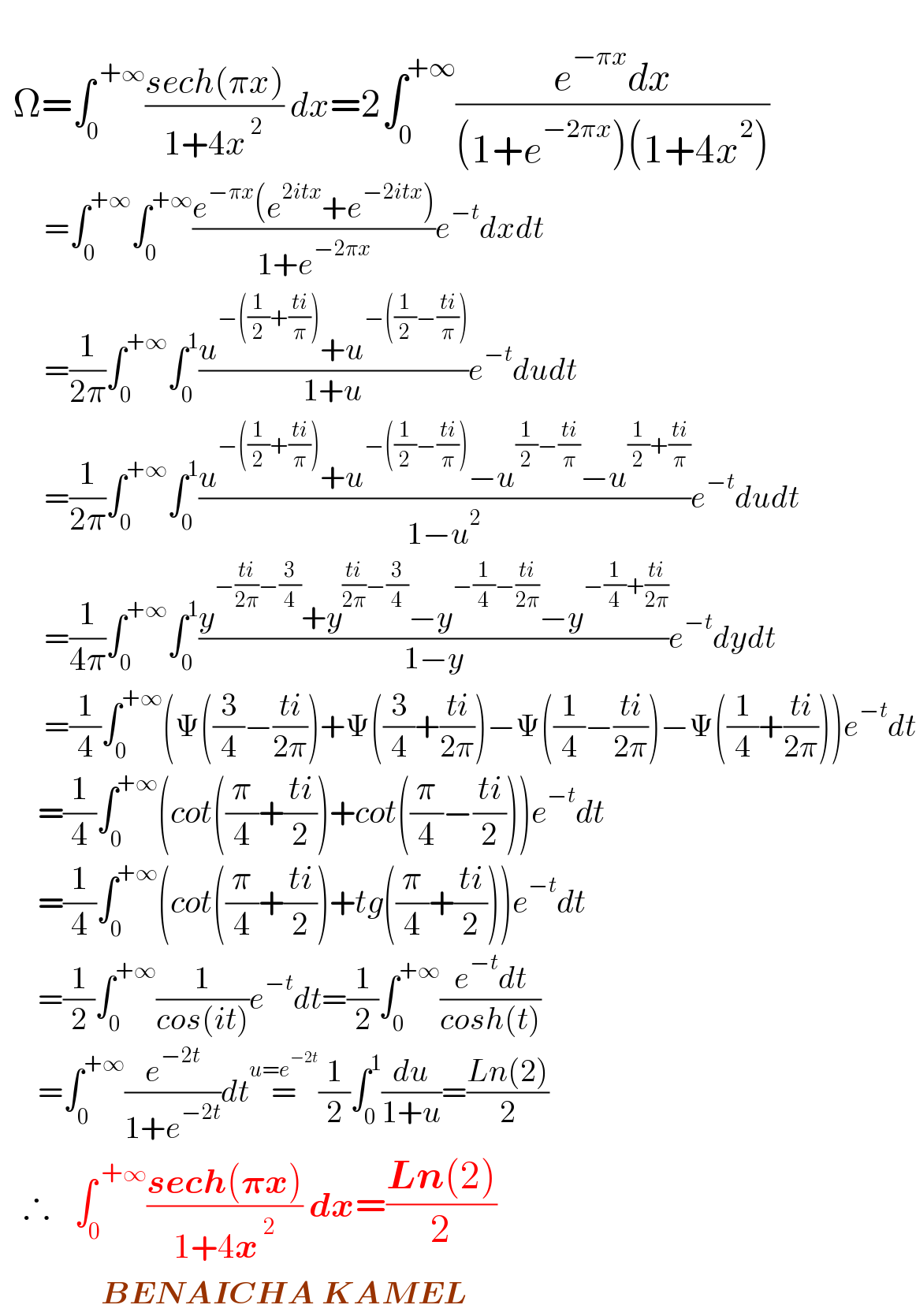
Ω=∫_0 ^( +∞) ((sech(πx))/(1+4x^( 2) )) dx=2∫_0 ^(+∞) ((e^(−πx) dx)/((1+e^(−2πx) )(1+4x^2 ))) =∫_0 ^(+∞) ∫_0 ^(+∞) ((e^(−πx) (e^(2itx) +e^(−2itx) ))/(1+e^(−2πx) ))e^(−t) dxdt =(1/(2π))∫_0 ^(+∞) ∫_0 ^1 ((u^(−((1/2)+((ti)/π))) +u^(−((1/2)−((ti)/π))) )/(1+u))e^(−t) dudt =(1/(2π))∫_0 ^(+∞) ∫_0 ^1 ((u^(−((1/2)+((ti)/π))) +u^(−((1/2)−((ti)/π))) −u^((1/2)−((ti)/π)) −u^((1/2)+((ti)/π)) )/(1−u^2 ))e^(−t) dudt =(1/(4π))∫_0 ^(+∞) ∫_0 ^1 ((y^(−((ti)/(2π))−(3/4)) +y^(((ti)/(2π))−(3/4)) −y^(−(1/4)−((ti)/(2π))) −y^(−(1/4)+((ti)/(2π))) )/(1−y))e^(−t) dydt =(1/4)∫_0 ^(+∞) (Ψ((3/4)−((ti)/(2π)))+Ψ((3/4)+((ti)/(2π)))−Ψ((1/4)−((ti)/(2π)))−Ψ((1/4)+((ti)/(2π))))e^(−t) dt =(1/4)∫_0 ^(+∞) (cot((π/4)+((ti)/2))+cot((π/4)−((ti)/2)))e^(−t) dt =(1/4)∫_0 ^(+∞) (cot((π/4)+((ti)/2))+tg((π/4)+((ti)/2)))e^(−t) dt =(1/2)∫_0 ^(+∞) (1/(cos(it)))e^(−t) dt=(1/2)∫_0 ^(+∞) ((e^(−t) dt)/(cosh(t))) =∫_0 ^(+∞) (e^(−2t) /(1+e^(−2t) ))dt=^(u=e^(−2t) ) (1/2)∫_0 ^1 (du/(1+u))=((Ln(2))/2) ∴ ∫_0 ^( +∞) ((sech(𝛑x))/(1+4x^( 2) )) dx=((Ln(2))/2) BENAICHA KAMEL

$$ \\ $$$$\:\:\Omega=\int_{\mathrm{0}} ^{\:+\infty} \frac{{sech}\left(\pi{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\:\mathrm{2}} }\:{dx}=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−\pi{x}} {dx}}{\left(\mathrm{1}+{e}^{−\mathrm{2}\pi{x}} \right)\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−\pi{x}} \left({e}^{\mathrm{2}{itx}} +{e}^{−\mathrm{2}{itx}} \right)}{\mathrm{1}+{e}^{−\mathrm{2}\pi{x}} }{e}^{−{t}} {dxdt} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{ti}}{\pi}\right)} +{u}^{−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{ti}}{\pi}\right)} }{\mathrm{1}+{u}}{e}^{−{t}} {dudt} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{ti}}{\pi}\right)} +{u}^{−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{ti}}{\pi}\right)} −{u}^{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{ti}}{\pi}} −{u}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{ti}}{\pi}} }{\mathrm{1}−{u}^{\mathrm{2}} }{e}^{−{t}} {dudt} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}\pi}\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{y}^{−\frac{{ti}}{\mathrm{2}\pi}−\frac{\mathrm{3}}{\mathrm{4}}} +{y}^{\frac{{ti}}{\mathrm{2}\pi}−\frac{\mathrm{3}}{\mathrm{4}}} −{y}^{−\frac{\mathrm{1}}{\mathrm{4}}−\frac{{ti}}{\mathrm{2}\pi}} −{y}^{−\frac{\mathrm{1}}{\mathrm{4}}+\frac{{ti}}{\mathrm{2}\pi}} }{\mathrm{1}−{y}}{e}^{−{t}} {dydt} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{+\infty} \left(\Psi\left(\frac{\mathrm{3}}{\mathrm{4}}−\frac{{ti}}{\mathrm{2}\pi}\right)+\Psi\left(\frac{\mathrm{3}}{\mathrm{4}}+\frac{{ti}}{\mathrm{2}\pi}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{{ti}}{\mathrm{2}\pi}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{{ti}}{\mathrm{2}\pi}\right)\right){e}^{−{t}} {dt} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{+\infty} \left({cot}\left(\frac{\pi}{\mathrm{4}}+\frac{{ti}}{\mathrm{2}}\right)+{cot}\left(\frac{\pi}{\mathrm{4}}−\frac{{ti}}{\mathrm{2}}\right)\right){e}^{−{t}} {dt} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{+\infty} \left({cot}\left(\frac{\pi}{\mathrm{4}}+\frac{{ti}}{\mathrm{2}}\right)+{tg}\left(\frac{\pi}{\mathrm{4}}+\frac{{ti}}{\mathrm{2}}\right)\right){e}^{−{t}} {dt} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{{cos}\left({it}\right)}{e}^{−{t}} {dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{t}} {dt}}{{cosh}\left({t}\right)} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−\mathrm{2}{t}} }{\mathrm{1}+{e}^{−\mathrm{2}{t}} }{dt}\overset{{u}={e}^{−\mathrm{2}{t}} } {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\mathrm{1}+{u}}=\frac{{Ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\:\:\:\therefore\:\:\:\int_{\mathrm{0}} ^{\:+\infty} \frac{\boldsymbol{{sech}}\left(\boldsymbol{\pi{x}}\right)}{\mathrm{1}+\mathrm{4}\boldsymbol{{x}}^{\:\mathrm{2}} }\:\boldsymbol{{dx}}=\frac{\boldsymbol{{Ln}}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{BENAICHA}}\:\boldsymbol{{KAMEL}} \\ $$

Commented by Tawa11 last updated on 03/Aug/21

great

$$\mathrm{great} \\ $$

Commented by mindispower last updated on 03/Aug/21

nice solution sir

$${nice}\:{solution}\:{sir} \\ $$

Commented by mnjuly1970 last updated on 03/Aug/21

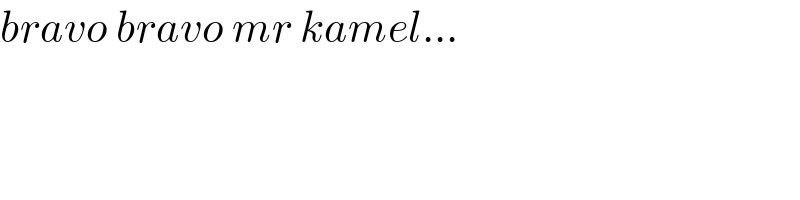
bravo bravo mr kamel...

$${bravo}\:{bravo}\:{mr}\:{kamel}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com