Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 149342 by MJS_new last updated on 04/Aug/21

$$\mathrm{is}\mathrm{this}\mathrm{true}\mathrm{and}\mathrm{is}\mathrm{there}\mathrm{a}\mathrm{proof}?$$ $$\mathrm{\forall }k\in \mathbb{N}\mid k>1$$ $$\frac{\underset{n=1}{\sum ^{k^2-1}}\sqrt{k+\sqrt{n}}}{\underset{n=1}{\sum ^{k^2-1}}\sqrt{k-\sqrt{n}}}=1+\sqrt{2}$$

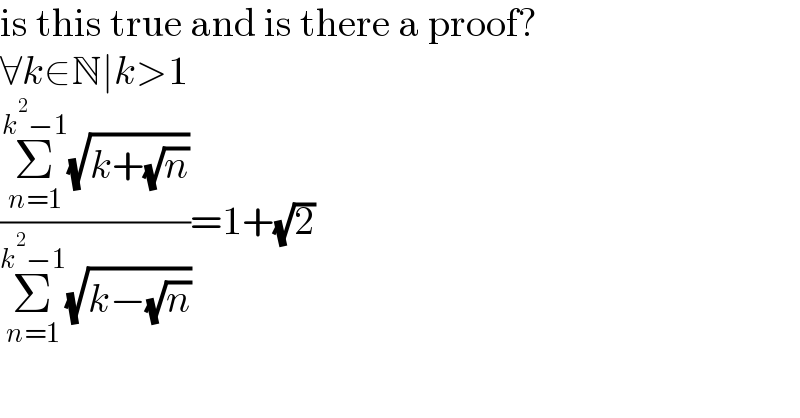
Commented bymr W last updated on 04/Aug/21

$$yes,{it}^{\prime }strue.$$

Answered by mr W last updated on 04/Aug/21

$$proof:$$ $${(\sqrt{k+\sqrt{n}}-\sqrt{k-\sqrt{n}})}^2=2(k-\sqrt{k^2-n})$$ $$\sqrt{k+\sqrt{n}}-\sqrt{k-\sqrt{n}}=\sqrt{2}\times \sqrt{k-\sqrt{k^2-n}}$$ $$\underset{n=1}{\sum ^{k^2-1}}\sqrt{k+\sqrt{n}}-\underset{n=1}{\sum ^{k^2-1}}\sqrt{k-\sqrt{n}}=\sqrt{2}\times \underset{n=k^2-1}{\sum ^1}\sqrt{k-\sqrt{k^2-n}}$$ $$\underset{n=1}{\sum ^{k^2-1}}\sqrt{k+\sqrt{n}}-\underset{n=1}{\sum ^{k^2-1}}\sqrt{k-\sqrt{n}}=\sqrt{2}\times \underset{n=1}{\sum ^{k^2-1}}\sqrt{k-\sqrt{n}}$$ $$\underset{n=1}{\sum ^{k^2-1}}\sqrt{k+\sqrt{n}}=(\sqrt{2}+1)\underset{n=1}{\sum ^{k^2-1}}\sqrt{k-\sqrt{n}}$$ $$\Rightarrow \frac{\underset{n=1}{\sum ^{k^2-1}}\sqrt{k+\sqrt{n}}}{\underset{n=1}{\sum ^{k^2-1}}\sqrt{k-\sqrt{n}}}=\sqrt{2}+1$$

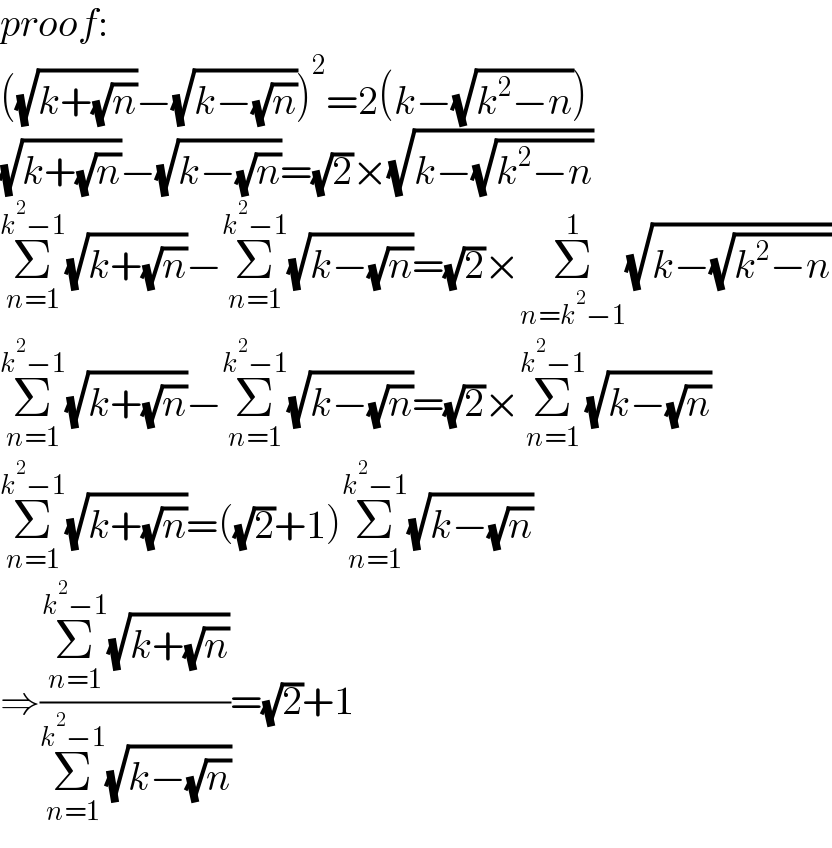
Commented byMJS_new last updated on 04/Aug/21

$$\mathrm{thank}\mathrm{you}!$$

Commented byTawa11 last updated on 06/Nov/21

$$\mathrm{great}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com