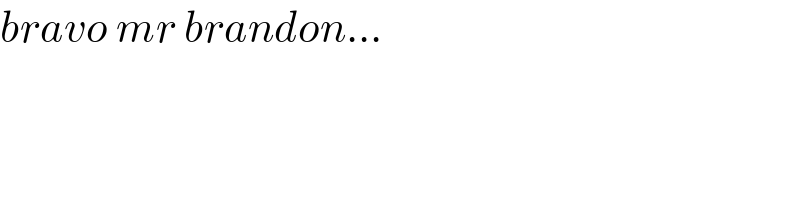Question and Answers Forum
Question Number 149673 by mnjuly1970 last updated on 06/Aug/21
![solve :: [ 1] 𝛗 := ∫_0 ^( ∞ ) ((ln^( 2) (e x ))/(e^( 4) +x^( 2) )) dx =((π k)/e^( 2) ) k:= ? [ 2 ] Ω := ∫_(0 ) ^( ∞) (( ln^( 3) (x ))/( e^( 2) + x^( 2) )) dx = ?](Q149673.png)
Answered by mathmax by abdo last updated on 06/Aug/21

Commented by Ar Brandon last updated on 07/Aug/21
Bravo ��
Commented by Tawa11 last updated on 06/Aug/21

Commented by Ar Brandon last updated on 06/Aug/21
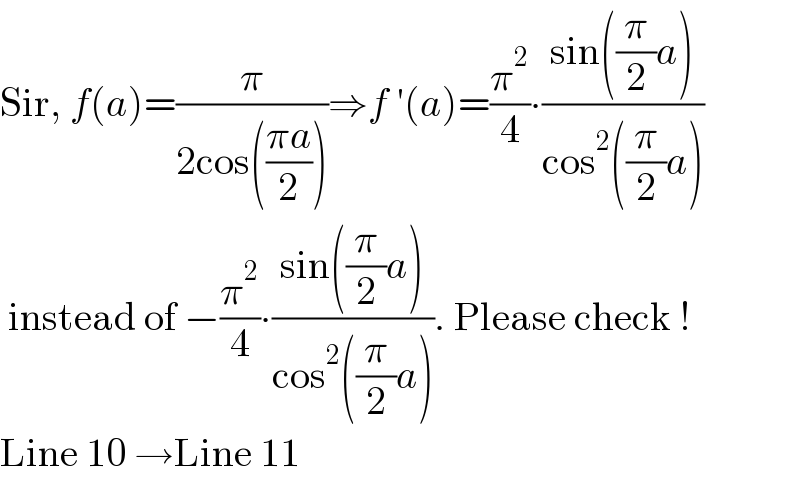
Commented by mathmax by abdo last updated on 07/Aug/21
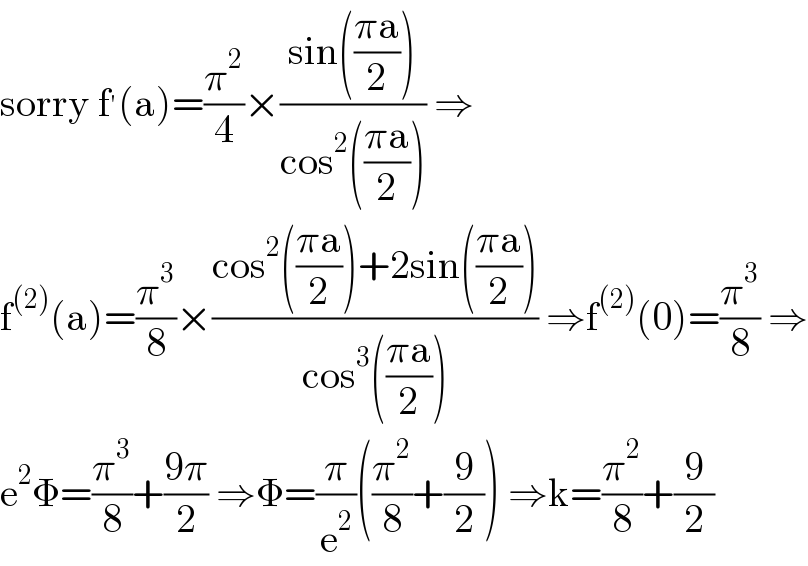
Commented by mathmax by abdo last updated on 07/Aug/21

Answered by Ar Brandon last updated on 06/Aug/21

Commented by Ar Brandon last updated on 06/Aug/21
It was a pleasure, Sir ��
Commented by mnjuly1970 last updated on 06/Aug/21
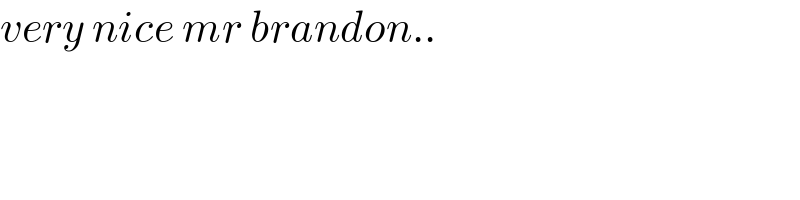
Answered by Ar Brandon last updated on 06/Aug/21

Commented by mnjuly1970 last updated on 06/Aug/21