
Question and Answers Forum
Question Number 149739 by iloveisrael last updated on 07/Aug/21
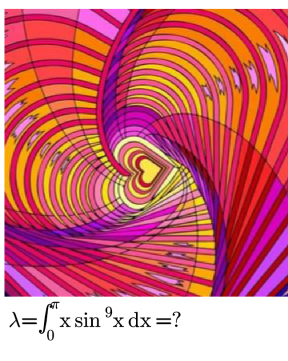
Answered by Olaf_Thorendsen last updated on 07/Aug/21
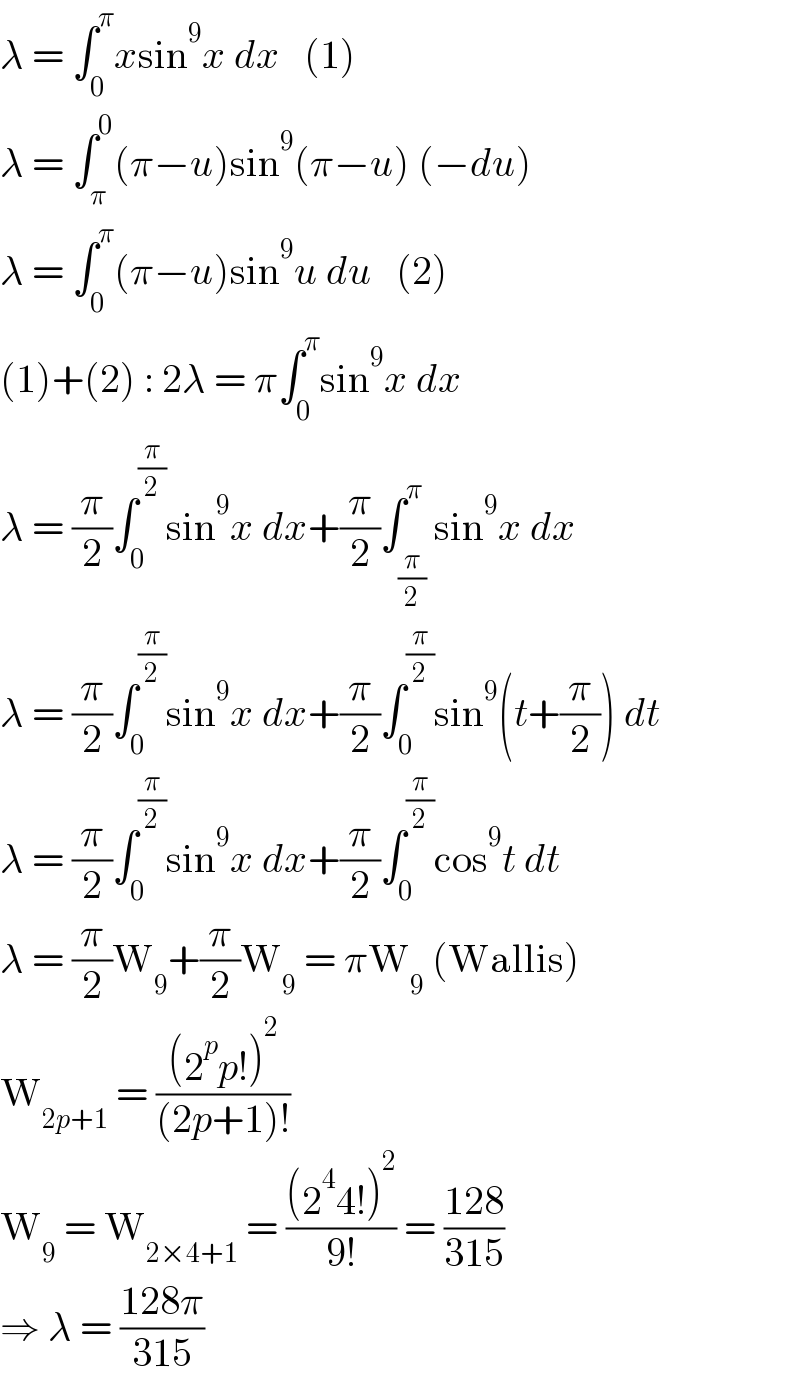
Answered by mathmax by abdo last updated on 07/Aug/21
![Ψ=∫_0 ^π x sin^9 x dx ⇒Ψ=∫_0 ^π x(((e^(ix) −e^(−ix) )/(2i)))^9 dx =(1/((2i)^9 ))∫_0 ^π x(Σ_(k=0) ^9 C_9 ^k (e^(ix) )^k (−e^(−ix) )^(9−k) )dx =(1/((2i)^9 ))Σ_(k=0) ^9 C_9 ^k (−1)^(9−k) ∫_0 ^π x e^(ikx) e^((k−9)ix) dx =−(1/((2i)^9 ))Σ_(k=0) ^9 (−1)^k C_9 ^k u_k u_k =∫_0 ^π x e^((2k−9)ix) dx =[(x/((2k−9)i))e^((2k−9)ix) ]_0 ^π −∫_0 ^π (1/((2k−9)i))e^((2k−9)ix) dx =(π/((2k−9)i))e^((2k−9)iπ) −(1/(((2k−9)i)^2 ))[e^((2k−9)ix) ]_0 ^π =−(π/((2k−9)i))+(1/((2k−9)^2 ))(−2) ⇒ Ψ=−(1/((2i)^9 ))Σ_(k=0) ^9 (−1)^k C_9 ^k (−(π/((2k−9)i))−(2/((2k−9)^2 )))....](Q149746.png)
Answered by gsk2684 last updated on 07/Aug/21
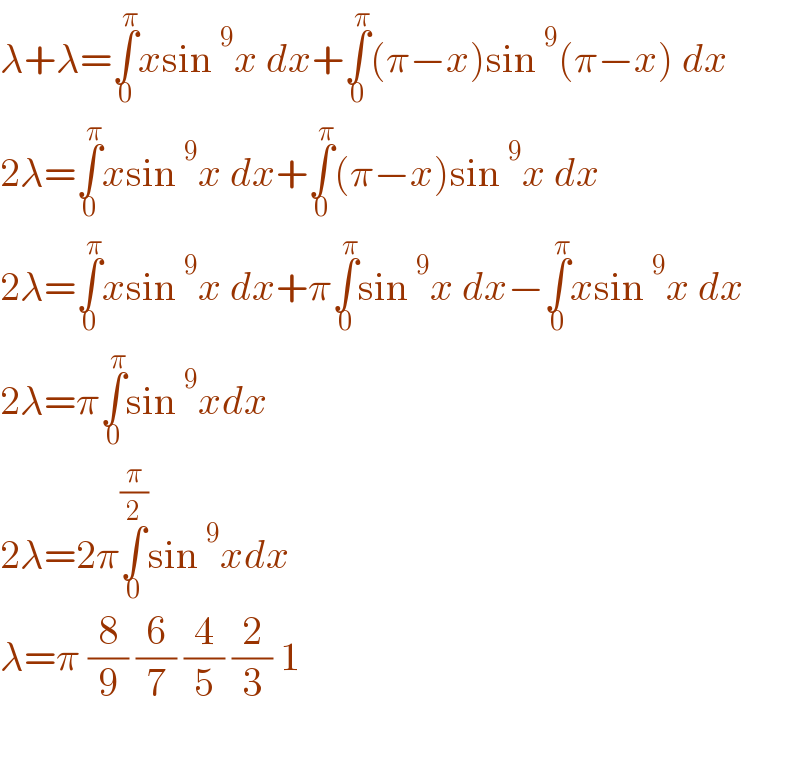
| ||
Question and Answers Forum | ||
Question Number 149739 by iloveisrael last updated on 07/Aug/21 | ||
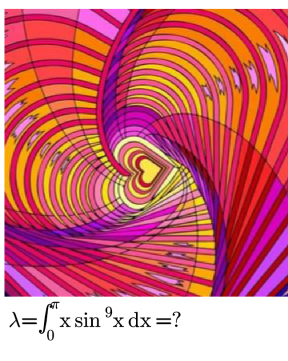 | ||
Answered by Olaf_Thorendsen last updated on 07/Aug/21 | ||
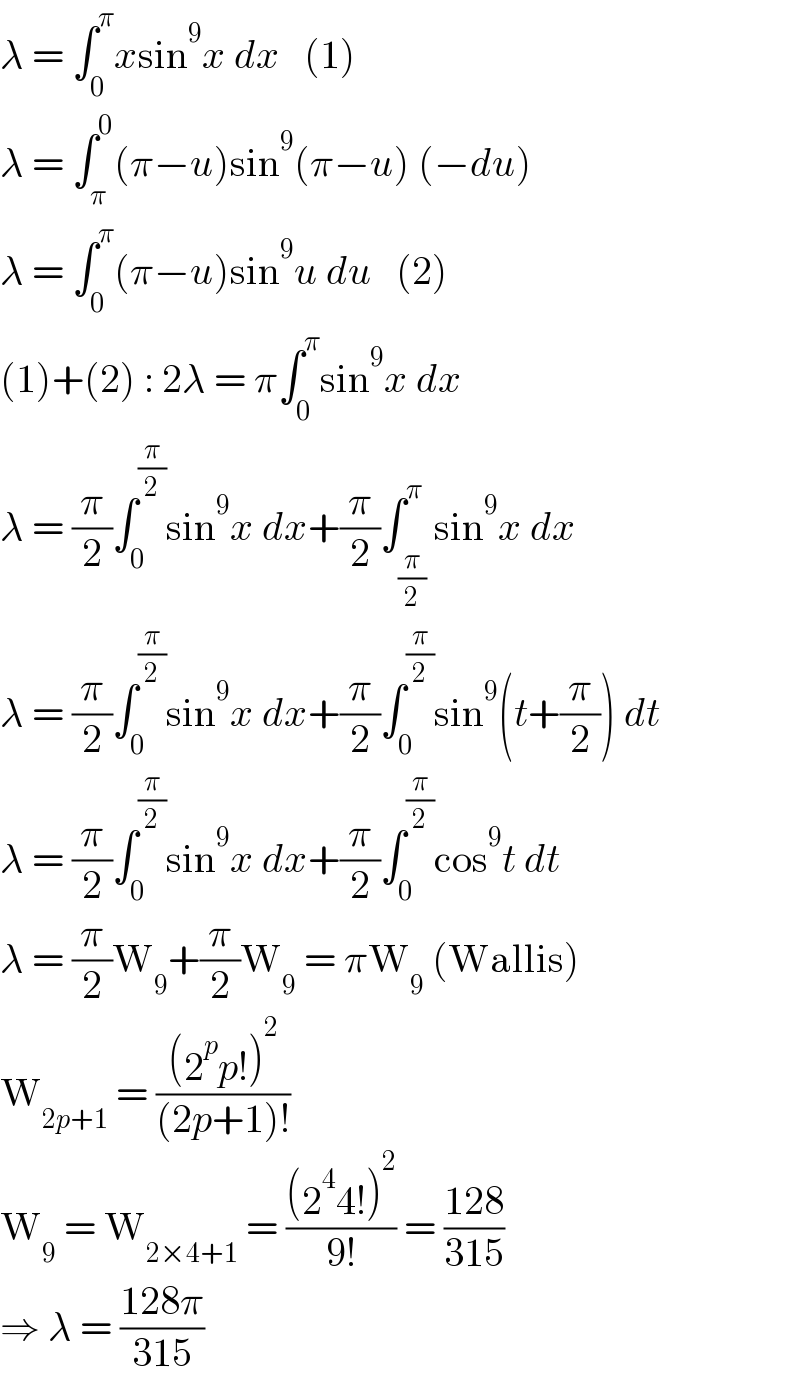 | ||
| ||
Answered by mathmax by abdo last updated on 07/Aug/21 | ||
![Ψ=∫_0 ^π x sin^9 x dx ⇒Ψ=∫_0 ^π x(((e^(ix) −e^(−ix) )/(2i)))^9 dx =(1/((2i)^9 ))∫_0 ^π x(Σ_(k=0) ^9 C_9 ^k (e^(ix) )^k (−e^(−ix) )^(9−k) )dx =(1/((2i)^9 ))Σ_(k=0) ^9 C_9 ^k (−1)^(9−k) ∫_0 ^π x e^(ikx) e^((k−9)ix) dx =−(1/((2i)^9 ))Σ_(k=0) ^9 (−1)^k C_9 ^k u_k u_k =∫_0 ^π x e^((2k−9)ix) dx =[(x/((2k−9)i))e^((2k−9)ix) ]_0 ^π −∫_0 ^π (1/((2k−9)i))e^((2k−9)ix) dx =(π/((2k−9)i))e^((2k−9)iπ) −(1/(((2k−9)i)^2 ))[e^((2k−9)ix) ]_0 ^π =−(π/((2k−9)i))+(1/((2k−9)^2 ))(−2) ⇒ Ψ=−(1/((2i)^9 ))Σ_(k=0) ^9 (−1)^k C_9 ^k (−(π/((2k−9)i))−(2/((2k−9)^2 )))....](Q149746.png) | ||
| ||
Answered by gsk2684 last updated on 07/Aug/21 | ||
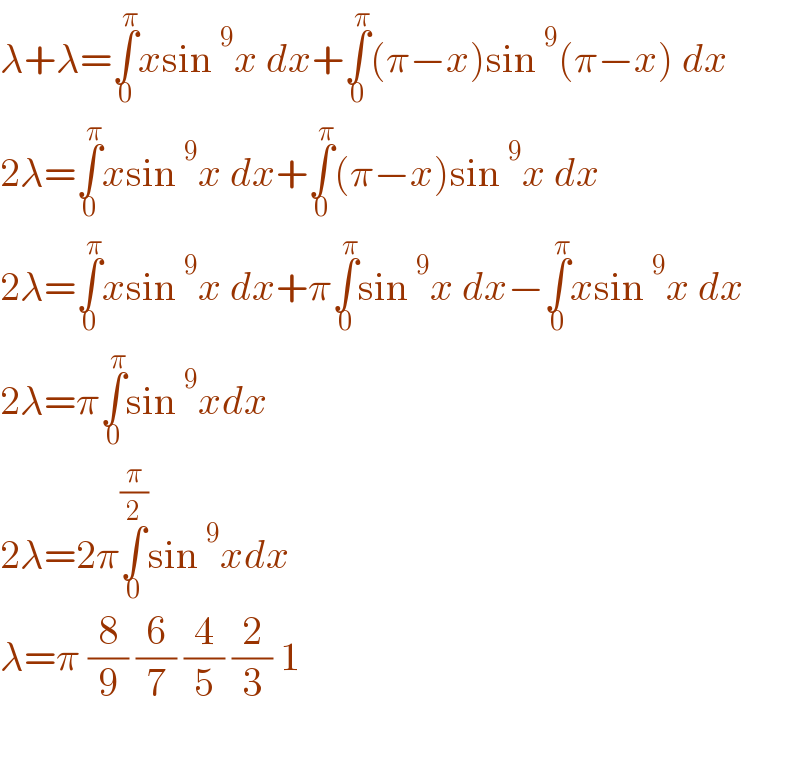 | ||
| ||