Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 149782 by iloveisrael last updated on 07/Aug/21

Answered by john_santu last updated on 07/Aug/21

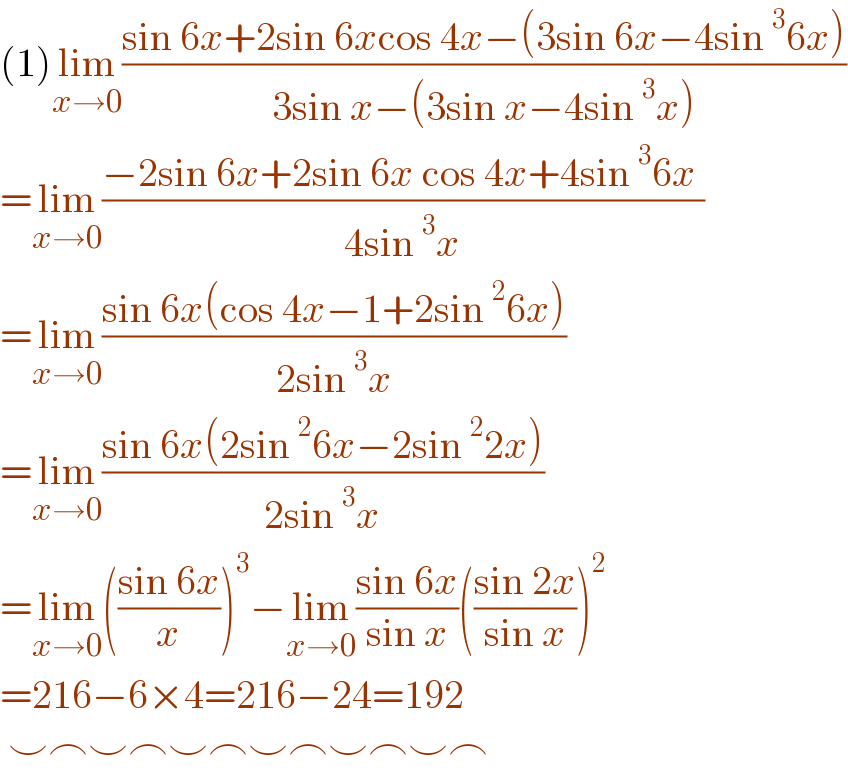
(1)lim_(x→0) ((sin 6x+2sin 6xcos 4x−(3sin 6x−4sin^3 6x))/(3sin x−(3sin x−4sin^3 x))) =lim_(x→0) ((−2sin 6x+2sin 6x cos 4x+4sin^3 6x )/(4sin^3 x)) =lim_(x→0) ((sin 6x(cos 4x−1+2sin^2 6x))/(2sin^3 x)) =lim_(x→0) ((sin 6x(2sin^2 6x−2sin^2 2x))/(2sin^3 x)) =lim_(x→0) (((sin 6x)/x))^3 −lim_(x→0) ((sin 6x)/(sin x))(((sin 2x)/(sin x)))^2 =216−6×4=216−24=192 ⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢

$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{6}{x}+\mathrm{2sin}\:\mathrm{6}{x}\mathrm{cos}\:\mathrm{4}{x}−\left(\mathrm{3sin}\:\mathrm{6}{x}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{6}{x}\right)}{\mathrm{3sin}\:{x}−\left(\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:\mathrm{6}{x}+\mathrm{2sin}\:\mathrm{6}{x}\:\mathrm{cos}\:\mathrm{4}{x}+\mathrm{4sin}\:^{\mathrm{3}} \mathrm{6}{x}\:}{\mathrm{4sin}\:^{\mathrm{3}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{6}{x}\left(\mathrm{cos}\:\mathrm{4}{x}−\mathrm{1}+\mathrm{2sin}\:^{\mathrm{2}} \mathrm{6}{x}\right)}{\mathrm{2sin}\:^{\mathrm{3}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{6}{x}\left(\mathrm{2sin}\:^{\mathrm{2}} \mathrm{6}{x}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}\right)}{\mathrm{2sin}\:^{\mathrm{3}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{6}{x}}{{x}}\right)^{\mathrm{3}} −\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{6}{x}}{\mathrm{sin}\:{x}}\left(\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{sin}\:{x}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{216}−\mathrm{6}×\mathrm{4}=\mathrm{216}−\mathrm{24}=\mathrm{192} \\ $$$$\:\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown \\ $$

Answered by john_santu last updated on 08/Aug/21

(2)lim_(x→0) ((1−cos ((π/2)x+sin x))/(2x^2 )) = lim_(x→0) ((2sin^2 (((πx+2sin x)/4)))/(2x^2 )) =lim_(x→0) (((sin (((πx+2sin x)/4)))/((πx+2sin x)/4)))^2 ×lim_(x→0) ((((πx+2sin x)/4)/x))^2 =lim_(x→0) (((πx+2sin x)/(4x)))^2 = (((π+2)/4))^2 =(((π+2)^2 )/(16))

$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}{x}+\mathrm{sin}\:{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\pi{x}+\mathrm{2sin}\:{x}}{\mathrm{4}}\right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\left(\frac{\pi{x}+\mathrm{2sin}\:{x}}{\mathrm{4}}\right)}{\frac{\pi{x}+\mathrm{2sin}\:{x}}{\mathrm{4}}}\right)^{\mathrm{2}} ×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{\pi{x}+\mathrm{2sin}\:{x}}{\mathrm{4}}}{{x}}\right)^{\mathrm{2}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\pi{x}+\mathrm{2sin}\:{x}}{\mathrm{4}{x}}\right)^{\mathrm{2}} =\:\left(\frac{\pi+\mathrm{2}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$=\frac{\left(\pi+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{16}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com