
Question Number 149817 by ajfour last updated on 07/Aug/21
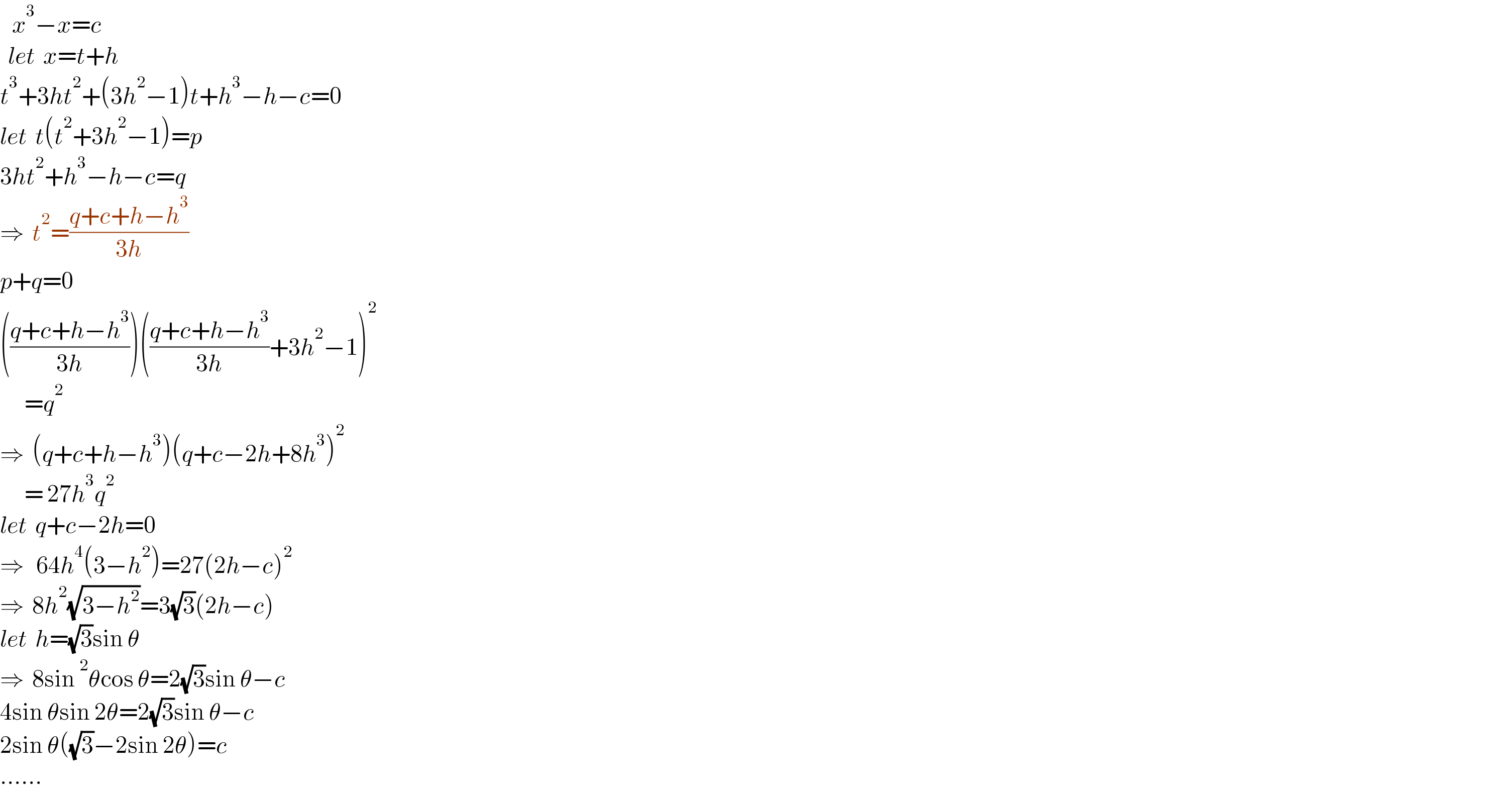
$$\:\:\:{x}^{\mathrm{3}} −{x}={c} \\ $$$$\:\:{let}\:\:{x}={t}+{h} \\ $$$${t}^{\mathrm{3}} +\mathrm{3}{ht}^{\mathrm{2}} +\left(\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right){t}+{h}^{\mathrm{3}} −{h}−{c}=\mathrm{0} \\ $$$${let}\:\:{t}\left({t}^{\mathrm{2}} +\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right)={p} \\ $$$$\mathrm{3}{ht}^{\mathrm{2}} +{h}^{\mathrm{3}} −{h}−{c}={q} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{2}} =\frac{{q}+{c}+{h}−{h}^{\mathrm{3}} }{\mathrm{3}{h}} \\ $$$${p}+{q}=\mathrm{0} \\ $$$$\left(\frac{{q}+{c}+{h}−{h}^{\mathrm{3}} }{\mathrm{3}{h}}\right)\left(\frac{{q}+{c}+{h}−{h}^{\mathrm{3}} }{\mathrm{3}{h}}+\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:={q}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left({q}+{c}+{h}−{h}^{\mathrm{3}} \right)\left({q}+{c}−\mathrm{2}{h}+\mathrm{8}{h}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{27}{h}^{\mathrm{3}} {q}^{\mathrm{2}} \\ $$$${let}\:\:{q}+{c}−\mathrm{2}{h}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{64}{h}^{\mathrm{4}} \left(\mathrm{3}−{h}^{\mathrm{2}} \right)=\mathrm{27}\left(\mathrm{2}{h}−{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{8}{h}^{\mathrm{2}} \sqrt{\mathrm{3}−{h}^{\mathrm{2}} }=\mathrm{3}\sqrt{\mathrm{3}}\left(\mathrm{2}{h}−{c}\right) \\ $$$${let}\:\:{h}=\sqrt{\mathrm{3}}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{8sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:\theta=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−{c} \\ $$$$\mathrm{4sin}\:\theta\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−{c} \\ $$$$\mathrm{2sin}\:\theta\left(\sqrt{\mathrm{3}}−\mathrm{2sin}\:\mathrm{2}\theta\right)={c} \\ $$$$...... \\ $$
