Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 149870 by mathdanisur last updated on 07/Aug/21

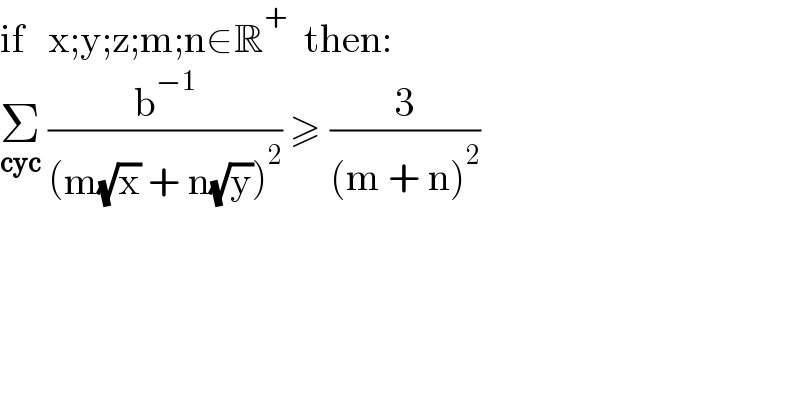
if x;y;z;m;n∈R^+ then: Σ_(cyc) (b^(−1) /((m(√x) + n(√y))^2 )) ≥ (3/((m + n)^2 ))

$$\mathrm{if}\:\:\:\mathrm{x};\mathrm{y};\mathrm{z};\mathrm{m};\mathrm{n}\in\mathbb{R}^{+} \:\:\mathrm{then}: \\ $$$$\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{b}^{−\mathrm{1}} }{\left(\mathrm{m}\sqrt{\mathrm{x}}\:+\:\mathrm{n}\sqrt{\mathrm{y}}\right)^{\mathrm{2}} }\:\geqslant\:\frac{\mathrm{3}}{\left(\mathrm{m}\:+\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$

Commented by mathdanisur last updated on 08/Aug/21

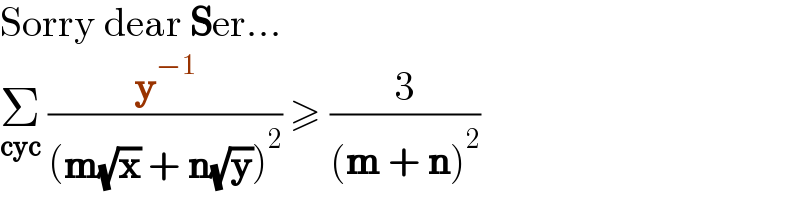
Sorry dear Ser... Σ_(cyc) (y^(−1) /((m(√x) + n(√y))^2 )) ≥ (3/((m + n)^2 ))

$$\mathrm{Sorry}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}... \\ $$$$\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\boldsymbol{\mathrm{y}}^{−\mathrm{1}} }{\left(\boldsymbol{\mathrm{m}}\sqrt{\boldsymbol{\mathrm{x}}}\:+\:\boldsymbol{\mathrm{n}}\sqrt{\boldsymbol{\mathrm{y}}}\right)^{\mathrm{2}} }\:\geqslant\:\frac{\mathrm{3}}{\left(\boldsymbol{\mathrm{m}}\:+\:\boldsymbol{\mathrm{n}}\right)^{\mathrm{2}} } \\ $$

Commented by mathdanisur last updated on 08/Aug/21

Σ_(cyc) (y^(−1) /((m(√x)+n(√y))^2 ))≥^(am-gm) Σ_(cyc) (1/((((m(x+y))/2)+ny)^2 )) = 4Σ_(cyc) (1/((mx+(m+2n)y)^2 )) ≥ 4∙(((1+1+1)^3 )/((Σ_(cyc) (mx+(m+2n)y)^2 )) = ((27)/((m+n)^2 (x+y+z)^2 )) (1) 3=x^2 +y^2 +z^2 ≥(((x+y+z)^2 )/3) ⇔ 9≥(x+y+z)^2 (2) (1) and (2) we obtain Σ_(cyc) (y^(−1) /((m(√x)+n(√y))^2 ))≥((27)/((n+m)^2 ∙9))=(3/((m+n)^2 )) Dear Ser, wrong or true.?

$$\underset{{cyc}} {\sum}\frac{{y}^{−\mathrm{1}} }{\left({m}\sqrt{{x}}+{n}\sqrt{{y}}\right)^{\mathrm{2}} }\overset{{am}-{gm}} {\geqslant}\underset{{cyc}} {\sum}\frac{\mathrm{1}}{\left(\frac{{m}\left({x}+{y}\right)}{\mathrm{2}}+{ny}\right)^{\mathrm{2}} }\:=\:\mathrm{4}\underset{{cyc}} {\sum}\frac{\mathrm{1}}{\left({mx}+\left({m}+\mathrm{2}{n}\right){y}\right)^{\mathrm{2}} } \\ $$$$\geqslant\:\mathrm{4}\centerdot\frac{\left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{3}} }{\left(\underset{{cyc}} {\sum}\left({mx}+\left({m}+\mathrm{2}{n}\right){y}\right)^{\mathrm{2}} \right.}\:=\:\frac{\mathrm{27}}{\left({m}+{n}\right)^{\mathrm{2}} \left({x}+{y}+{z}\right)^{\mathrm{2}} }\:\left(\mathrm{1}\right) \\ $$$$\mathrm{3}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \geqslant\frac{\left({x}+{y}+{z}\right)^{\mathrm{2}} }{\mathrm{3}}\:\Leftrightarrow\:\mathrm{9}\geqslant\left({x}+{y}+{z}\right)^{\mathrm{2}} \:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\:{we}\:{obtain}\:\underset{{cyc}} {\sum}\frac{{y}^{−\mathrm{1}} }{\left({m}\sqrt{{x}}+{n}\sqrt{{y}}\right)^{\mathrm{2}} }\geqslant\frac{\mathrm{27}}{\left({n}+{m}\right)^{\mathrm{2}} \centerdot\mathrm{9}}=\frac{\mathrm{3}}{\left({m}+{n}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Dear}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{wrong}\:\mathrm{or}\:\mathrm{true}.? \\ $$

Commented by mathdanisur last updated on 08/Aug/21

Thank you very much dear Ser...

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com