Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 1499 by 112358 last updated on 14/Aug/15

Use the ε−δ definition of the limit to show that lim_(x→3) (x/(6−x))=1 . (I′m hoping to better understand this concept by example so please help me by explaning the reasoning behind your steps.)

$${Use}\:{the}\:\epsilon−\delta\:{definition}\:{of}\:{the} \\ $$$${limit}\:{to}\:{show}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{{x}}{\mathrm{6}−{x}}=\mathrm{1}\:. \\ $$$$\left({I}'{m}\:{hoping}\:{to}\:{better}\:{understand}\right. \\ $$$${this}\:{concept}\:{by}\:{example}\:{so}\:{please} \\ $$$${help}\:{me}\:{by}\:{explaning}\:{the}\: \\ $$$$\left.{reasoning}\:{behind}\:{your}\:{steps}.\right) \\ $$

Commented by 123456 last updated on 14/Aug/15

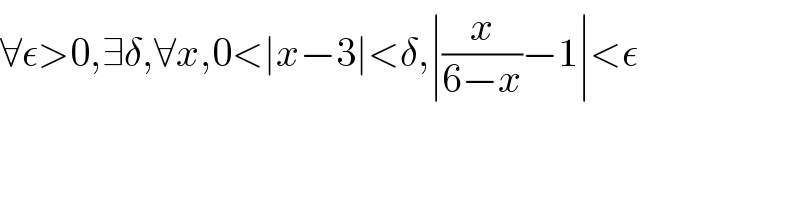
∀ε>0,∃δ,∀x,0<∣x−3∣<δ,∣(x/(6−x))−1∣<ε

$$\forall\epsilon>\mathrm{0},\exists\delta,\forall{x},\mathrm{0}<\mid{x}−\mathrm{3}\mid<\delta,\mid\frac{{x}}{\mathrm{6}−{x}}−\mathrm{1}\mid<\epsilon \\ $$

Commented by 123456 last updated on 14/Aug/15

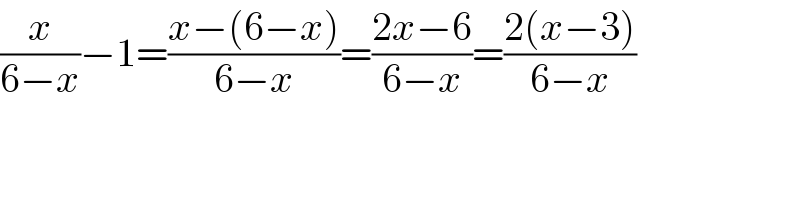
(x/(6−x))−1=((x−(6−x))/(6−x))=((2x−6)/(6−x))=((2(x−3))/(6−x))

$$\frac{{x}}{\mathrm{6}−{x}}−\mathrm{1}=\frac{{x}−\left(\mathrm{6}−{x}\right)}{\mathrm{6}−{x}}=\frac{\mathrm{2}{x}−\mathrm{6}}{\mathrm{6}−{x}}=\frac{\mathrm{2}\left({x}−\mathrm{3}\right)}{\mathrm{6}−{x}} \\ $$

Commented by 123456 last updated on 14/Aug/15

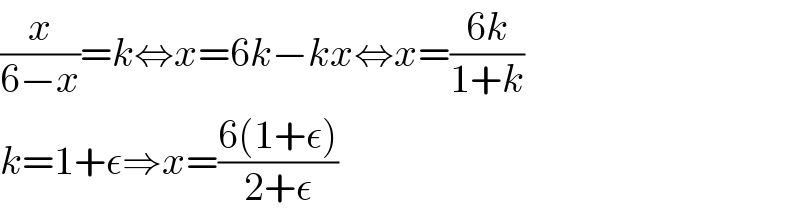
(x/(6−x))=k⇔x=6k−kx⇔x=((6k)/(1+k)) k=1+ε⇒x=((6(1+ε))/(2+ε))

$$\frac{{x}}{\mathrm{6}−{x}}={k}\Leftrightarrow{x}=\mathrm{6}{k}−{kx}\Leftrightarrow{x}=\frac{\mathrm{6}{k}}{\mathrm{1}+{k}} \\ $$$${k}=\mathrm{1}+\epsilon\Rightarrow{x}=\frac{\mathrm{6}\left(\mathrm{1}+\epsilon\right)}{\mathrm{2}+\epsilon} \\ $$

Answered by 123456 last updated on 16/Aug/15

lim_(x→3) (x/(6−x))=1⇒∃ε>0,∀δ,0<∣x−3∣<δ⇒∣(x/(6−x))−1∣<ε lets simplyfy things a little ∣(x/(6−x))−1∣=∣((x−(6−x))/(6−x))∣=∣((x−6+x)/(6−x))∣=∣((2x−6)/(6−x))∣ =((2∣x−3∣)/(∣6−x∣))<ε ∣x−3∣<((∣6−x∣ε)/2) then ∣x−3∣<1⇒2<x<4⇒−4<x<−2⇒2<6−x<4⇒2<∣6−x∣<4 ∣x−3∣<((∣6−x∣ε)/2)<((2ε)/2)=ε then lets δ=min(1,ε) if δ=1, then 1<ε⇒ε>1 ∣x−3∣<1⇒((2∣x−3∣)/(∣6−x∣))<(2/(∣6−x∣)) 2<x<4⇒2<6−x<4⇒(1/4)<(1/(6−x))<(1/2)⇒(1/4)<(1/(∣6−x∣))<(1/2) ((2∣x−3∣)/(∣6−x∣))<(2/(∣6−x∣))<(2/2)<1<ε ∣(x/(6−x))−1∣<ε then suppose that δ=ε ∣x−3∣<δ⇒((2∣x−3∣)/(∣6−x∣))<((2ε)/2)=ε ∣(x/(6−x))−1∣<ε

$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{{x}}{\mathrm{6}−{x}}=\mathrm{1}\Rightarrow\exists\epsilon>\mathrm{0},\forall\delta,\mathrm{0}<\mid{x}−\mathrm{3}\mid<\delta\Rightarrow\mid\frac{{x}}{\mathrm{6}−{x}}−\mathrm{1}\mid<\epsilon \\ $$$$\mathrm{lets}\:\mathrm{simplyfy}\:\mathrm{things}\:\mathrm{a}\:\mathrm{little} \\ $$$$\mid\frac{{x}}{\mathrm{6}−{x}}−\mathrm{1}\mid=\mid\frac{{x}−\left(\mathrm{6}−{x}\right)}{\mathrm{6}−{x}}\mid=\mid\frac{{x}−\mathrm{6}+{x}}{\mathrm{6}−{x}}\mid=\mid\frac{\mathrm{2}{x}−\mathrm{6}}{\mathrm{6}−{x}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\mid{x}−\mathrm{3}\mid}{\mid\mathrm{6}−{x}\mid}<\epsilon \\ $$$$\mid{x}−\mathrm{3}\mid<\frac{\mid\mathrm{6}−{x}\mid\epsilon}{\mathrm{2}} \\ $$$$\mathrm{then} \\ $$$$\mid{x}−\mathrm{3}\mid<\mathrm{1}\Rightarrow\mathrm{2}<{x}<\mathrm{4}\Rightarrow−\mathrm{4}<{x}<−\mathrm{2}\Rightarrow\mathrm{2}<\mathrm{6}−{x}<\mathrm{4}\Rightarrow\mathrm{2}<\mid\mathrm{6}−{x}\mid<\mathrm{4} \\ $$$$\mid{x}−\mathrm{3}\mid<\frac{\mid\mathrm{6}−{x}\mid\epsilon}{\mathrm{2}}<\frac{\mathrm{2}\epsilon}{\mathrm{2}}=\epsilon \\ $$$$\mathrm{then}\:\mathrm{lets} \\ $$$$\delta=\mathrm{min}\left(\mathrm{1},\epsilon\right) \\ $$$$\mathrm{if}\:\delta=\mathrm{1},\:\mathrm{then}\:\mathrm{1}<\epsilon\Rightarrow\epsilon>\mathrm{1} \\ $$$$\mid{x}−\mathrm{3}\mid<\mathrm{1}\Rightarrow\frac{\mathrm{2}\mid{x}−\mathrm{3}\mid}{\mid\mathrm{6}−{x}\mid}<\frac{\mathrm{2}}{\mid\mathrm{6}−{x}\mid} \\ $$$$\mathrm{2}<{x}<\mathrm{4}\Rightarrow\mathrm{2}<\mathrm{6}−{x}<\mathrm{4}\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}<\frac{\mathrm{1}}{\mathrm{6}−{x}}<\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}<\frac{\mathrm{1}}{\mid\mathrm{6}−{x}\mid}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{2}\mid{x}−\mathrm{3}\mid}{\mid\mathrm{6}−{x}\mid}<\frac{\mathrm{2}}{\mid\mathrm{6}−{x}\mid}<\frac{\mathrm{2}}{\mathrm{2}}<\mathrm{1}<\epsilon \\ $$$$\mid\frac{{x}}{\mathrm{6}−{x}}−\mathrm{1}\mid<\epsilon \\ $$$$\mathrm{then}\:\mathrm{suppose}\:\mathrm{that}\:\delta=\epsilon \\ $$$$\mid{x}−\mathrm{3}\mid<\delta\Rightarrow\frac{\mathrm{2}\mid{x}−\mathrm{3}\mid}{\mid\mathrm{6}−{x}\mid}<\frac{\mathrm{2}\epsilon}{\mathrm{2}}=\epsilon \\ $$$$\mid\frac{{x}}{\mathrm{6}−{x}}−\mathrm{1}\mid<\epsilon \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com