Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 149959 by Mathfinity last updated on 08/Aug/21

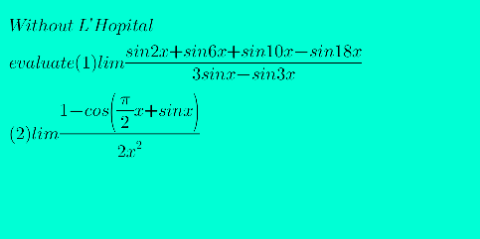
Commented by john_santu last updated on 08/Aug/21

Commented by john_santu last updated on 08/Aug/21

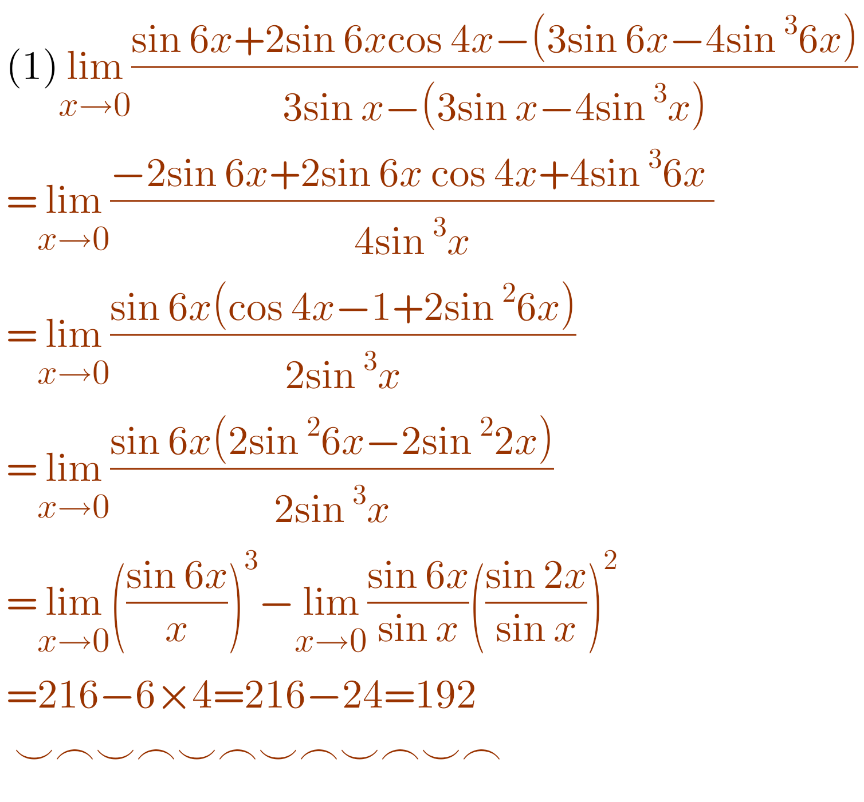
Commented by john_santu last updated on 08/Aug/21

why do you take mr iloveisrael's question?

$$ \\ $$why do you take mr iloveisrael's question?

Answered by gsk2684 last updated on 08/Aug/21

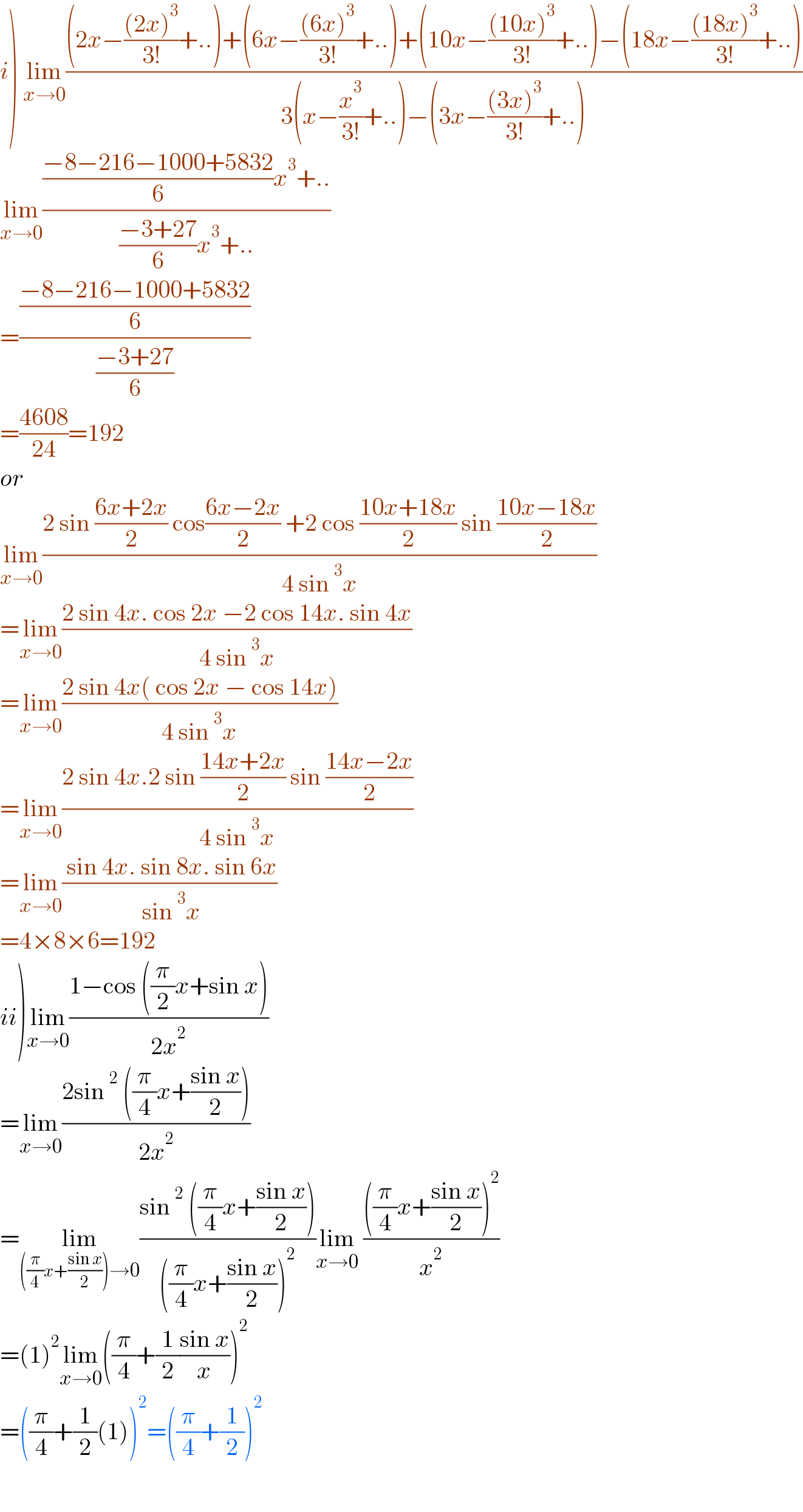
i) lim_(x→0) (((2x−(((2x)^3 )/(3!))+..)+(6x−(((6x)^3 )/(3!))+..)+(10x−(((10x)^3 )/(3!))+..)−(18x−(((18x)^3 )/(3!))+..))/(3(x−(x^3 /(3!))+..)−(3x−(((3x)^3 )/(3!))+..))) lim_(x→0) ((((−8−216−1000+5832)/6)x^3 +..)/(((−3+27)/6)x^3 +..)) =(((−8−216−1000+5832)/6)/((−3+27)/6)) =((4608)/(24))=192 or lim_(x→0) ((2 sin ((6x+2x)/2) cos((6x−2x)/2) +2 cos ((10x+18x)/2) sin ((10x−18x)/2))/(4 sin^3 x)) =lim_(x→0) ((2 sin 4x. cos 2x −2 cos 14x. sin 4x)/(4 sin^3 x)) =lim_(x→0) ((2 sin 4x( cos 2x − cos 14x))/(4 sin^3 x)) =lim_(x→0) ((2 sin 4x.2 sin ((14x+2x)/2) sin ((14x−2x)/2))/(4 sin^3 x)) =lim_(x→0) (( sin 4x. sin 8x. sin 6x)/( sin^3 x)) =4×8×6=192 ii)lim_(x→0) ((1−cos ((π/2)x+sin x))/(2x^2 )) =lim_(x→0) ((2sin^2 ((π/4)x+((sin x)/2)))/(2x^2 )) =lim_(((π/4)x+((sin x)/2))→0) ((sin^2 ((π/4)x+((sin x)/2)))/(((π/4)x+((sin x)/2))^2 ))lim_(x→0) ((((π/4)x+((sin x)/2))^2 )/x^2 ) =(1)^2 lim_(x→0) ((π/4)+(1/2)((sin x)/x))^2 =((π/4)+(1/2)(1))^2 =((π/4)+(1/2))^2

$$\left.{i}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{2}{x}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}+..\right)+\left(\mathrm{6}{x}−\frac{\left(\mathrm{6}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}+..\right)+\left(\mathrm{10}{x}−\frac{\left(\mathrm{10}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}+..\right)−\left(\mathrm{18}{x}−\frac{\left(\mathrm{18}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}+..\right)}{\mathrm{3}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+..\right)−\left(\mathrm{3}{x}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}+..\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{−\mathrm{8}−\mathrm{216}−\mathrm{1000}+\mathrm{5832}}{\mathrm{6}}{x}^{\mathrm{3}} +..}{\frac{−\mathrm{3}+\mathrm{27}}{\mathrm{6}}{x}^{\mathrm{3}} +..} \\ $$$$=\frac{\frac{−\mathrm{8}−\mathrm{216}−\mathrm{1000}+\mathrm{5832}}{\mathrm{6}}}{\frac{−\mathrm{3}+\mathrm{27}}{\mathrm{6}}} \\ $$$$=\frac{\mathrm{4608}}{\mathrm{24}}=\mathrm{192} \\ $$$${or} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{6}{x}+\mathrm{2}{x}}{\mathrm{2}}\:\mathrm{cos}\frac{\mathrm{6}{x}−\mathrm{2}{x}}{\mathrm{2}}\:+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{10}{x}+\mathrm{18}{x}}{\mathrm{2}}\:\mathrm{sin}\:\frac{\mathrm{10}{x}−\mathrm{18}{x}}{\mathrm{2}}}{\mathrm{4}\:\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{4}{x}.\:\mathrm{cos}\:\mathrm{2}{x}\:−\mathrm{2}\:\mathrm{cos}\:\mathrm{14}{x}.\:\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{4}\:\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{4}{x}\left(\:\mathrm{cos}\:\mathrm{2}{x}\:−\:\mathrm{cos}\:\mathrm{14}{x}\right)}{\mathrm{4}\:\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{4}{x}.\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{14}{x}+\mathrm{2}{x}}{\mathrm{2}}\:\mathrm{sin}\:\frac{\mathrm{14}{x}−\mathrm{2}{x}}{\mathrm{2}}}{\mathrm{4}\:\mathrm{sin}\:^{\mathrm{3}} {x}}\:\: \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\:\mathrm{sin}\:\mathrm{4}{x}.\:\mathrm{sin}\:\mathrm{8}{x}.\:\mathrm{sin}\:\mathrm{6}{x}}{\:\mathrm{sin}\:^{\mathrm{3}} {x}}\:\: \\ $$$$=\mathrm{4}×\mathrm{8}×\mathrm{6}=\mathrm{192} \\ $$$$\left.{ii}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}{x}+\mathrm{sin}\:{x}\right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{4}}{x}+\frac{\mathrm{sin}\:{x}}{\mathrm{2}}\right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\underset{\left(\frac{\pi}{\mathrm{4}}{x}+\frac{\mathrm{sin}\:{x}}{\mathrm{2}}\right)\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{4}}{x}+\frac{\mathrm{sin}\:{x}}{\mathrm{2}}\right)}{\left(\frac{\pi}{\mathrm{4}}{x}+\frac{\mathrm{sin}\:{x}}{\mathrm{2}}\right)^{\mathrm{2}} }\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\pi}{\mathrm{4}}{x}+\frac{\mathrm{sin}\:{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$=\left(\mathrm{1}\right)^{\mathrm{2}} \underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} \\ $$$$=\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\right)\right)^{\mathrm{2}} =\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$ \\ $$

Commented by john_santu last updated on 08/Aug/21

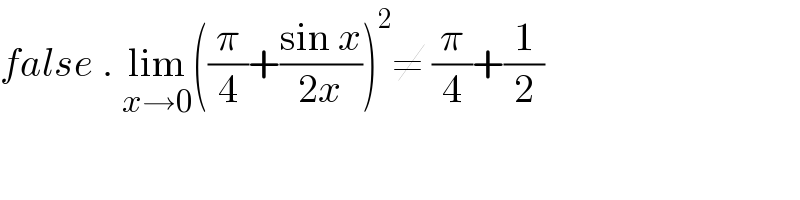
false . lim_(x→0) ((π/4)+((sin x)/(2x)))^2 ≠ (π/4)+(1/2)

$${false}\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{sin}\:{x}}{\mathrm{2}{x}}\right)^{\mathrm{2}} \neq\:\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com