
Question Number 150224 by mnjuly1970 last updated on 10/Aug/21

Answered by Olaf_Thorendsen last updated on 10/Aug/21
![I = ∫_0 ^1 (dx/(1+⌊(x/(1−x))⌋)) I = ∫_0 ^(+∞) (1/(1+⌊u⌋)).(du/((1+u)^2 )) I = Σ_(n=0) ^∞ ∫_n ^(n+1) (1/(1+n)).(du/((1+u)^2 )) I = Σ_(n=0) ^∞ (1/(n+1))[−(1/(1+u))]_n ^(n+1) I = Σ_(n=0) ^∞ (1/(n+1))((1/(n+1))−(1/(n+2))) I = Σ_(n=1) ^∞ (1/(n^2 (n+1))) I = Σ_(n=1) ^∞ ((1/n^2 )−(1/n)+(1/(n+1))) I = (π^2 /6)−1](Q150235.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+\lfloor\frac{{x}}{\mathrm{1}−{x}}\rfloor} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\mathrm{1}+\lfloor{u}\rfloor}.\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{n}}.\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}\left[−\frac{\mathrm{1}}{\mathrm{1}+{u}}\right]_{{n}} ^{{n}+\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 10/Aug/21
$$\:\:{thanks}\:{alot}\:{mr}\:{olaf}\:... \\ $$
Answered by Kamel last updated on 10/Aug/21
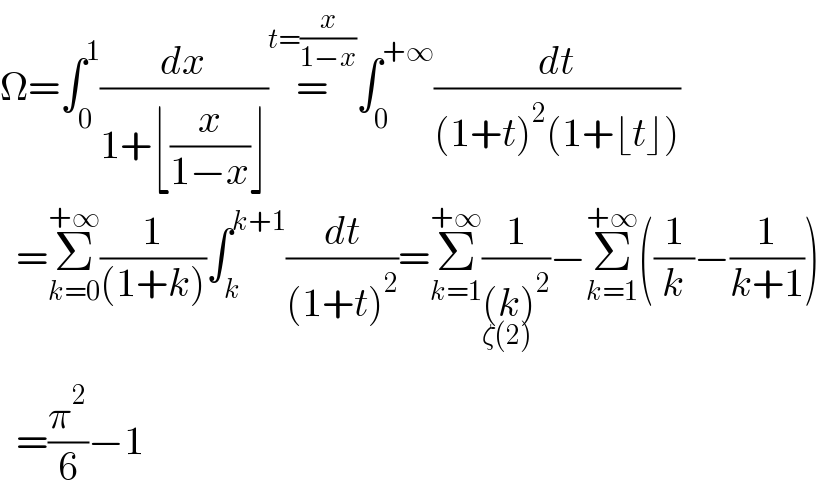
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+\lfloor\frac{{x}}{\mathrm{1}−{x}}\rfloor}\overset{{t}=\frac{{x}}{\mathrm{1}−{x}}} {=}\int_{\mathrm{0}} ^{+\infty} \frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} \left(\mathrm{1}+\lfloor{t}\rfloor\right)} \\ $$$$\:\:=\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{1}+{k}\right)}\int_{{k}} ^{{k}+\mathrm{1}} \frac{{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }=\underset{\zeta\left(\mathrm{2}\overset{} {\right)}} {\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({k}\right)^{\mathrm{2}} }−}\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$\:\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 10/Aug/21

$$\:\:\:\:{tashakor}\:{and}\:{mercey}.... \\ $$
