Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 150259 by mathdanisur last updated on 10/Aug/21

∫_( 0) ^( ∞) ((e^(−st) (cosh(2t)−cosh(5t))dt)/t)=?

$$\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{e}^{−\boldsymbol{\mathrm{st}}} \left(\mathrm{cosh}\left(\mathrm{2t}\right)−\mathrm{cosh}\left(\mathrm{5t}\right)\right)\mathrm{dt}}{\mathrm{t}}=? \\ $$

Answered by Ar Brandon last updated on 10/Aug/21

I(s)=∫_0 ^∞ ((e^(−st) (cosh(2t)−cosh(5t)))/t)dt I ′(s)=−∫_0 ^∞ e^(−st) (cosh(2t)−cosh(5t))dt =−(1/2)∫_0 ^∞ e^(−st) (e^(2t) +e^(−2t) −e^(5t) −e^(−5t) )dt =−(1/2)[(e^(−(s−2)t) /(2−s))−(e^(−(s+2)t) /(s+2))−(e^(−(s−5)t) /(5−s))+(e^(−(s+5)t) /(s+5))]_0 ^∞ =(1/2)((1/(2−s))−(1/(s+2))−(1/(5−s))+(1/(s+5))) I(s)=(1/2)(ln∣s+5∣+ln∣s−5∣−ln∣s+2∣−ln∣s−2∣)+C =(1/2)ln∣((s^2 −25)/(s^2 −4))∣+C. I(+∞)=0=C ⇒I(s)=(1/2)ln∣((s^2 −25)/(s^2 −4))∣

$${I}\left({s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{st}} \left(\mathrm{cosh}\left(\mathrm{2}{t}\right)−\mathrm{cosh}\left(\mathrm{5}{t}\right)\right)}{{t}}{dt} \\ $$$${I}\:'\left({s}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \left(\mathrm{cosh}\left(\mathrm{2}{t}\right)−\mathrm{cosh}\left(\mathrm{5}{t}\right)\right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \left({e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{t}} −{e}^{\mathrm{5}{t}} −{e}^{−\mathrm{5}{t}} \right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{e}^{−\left({s}−\mathrm{2}\right){t}} }{\mathrm{2}−{s}}−\frac{{e}^{−\left({s}+\mathrm{2}\right){t}} }{{s}+\mathrm{2}}−\frac{{e}^{−\left({s}−\mathrm{5}\right){t}} }{\mathrm{5}−{s}}+\frac{{e}^{−\left({s}+\mathrm{5}\right){t}} }{{s}+\mathrm{5}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}−{s}}−\frac{\mathrm{1}}{{s}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{5}−{s}}+\frac{\mathrm{1}}{{s}+\mathrm{5}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{I}\left({s}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\mid{s}+\mathrm{5}\mid+\mathrm{ln}\mid{s}−\mathrm{5}\mid−\mathrm{ln}\mid{s}+\mathrm{2}\mid−\mathrm{ln}\mid{s}−\mathrm{2}\mid\right)+{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{s}^{\mathrm{2}} −\mathrm{25}}{{s}^{\mathrm{2}} −\mathrm{4}}\mid+{C}.\:{I}\left(+\infty\right)=\mathrm{0}={C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{I}\left({s}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{s}^{\mathrm{2}} −\mathrm{25}}{{s}^{\mathrm{2}} −\mathrm{4}}\mid \\ $$

Commented by mathdanisur last updated on 10/Aug/21

Cool Ser, Thank You

$$\mathrm{Cool}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{Thank}\:{Y}\mathrm{ou} \\ $$

Commented by Ar Brandon last updated on 10/Aug/21

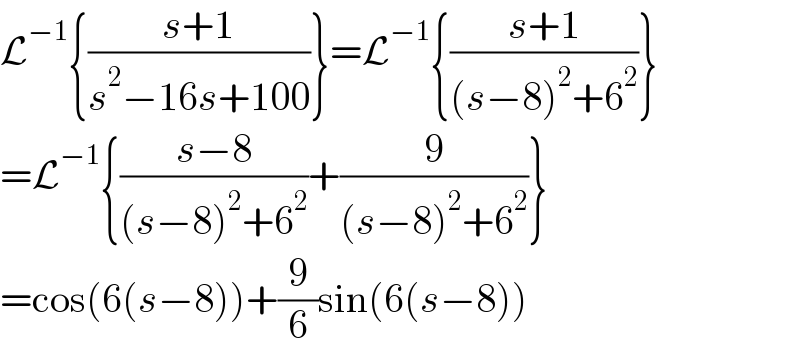
L^(−1) {((s+1)/(s^2 −16s+100))}=L^(−1) {((s+1)/((s−8)^2 +6^2 ))} =L^(−1) {((s−8)/((s−8)^2 +6^2 ))+(9/((s−8)^2 +6^2 ))} =cos(6(s−8))+(9/6)sin(6(s−8))

$$\mathcal{L}^{−\mathrm{1}} \left\{\frac{{s}+\mathrm{1}}{{s}^{\mathrm{2}} −\mathrm{16}{s}+\mathrm{100}}\right\}=\mathcal{L}^{−\mathrm{1}} \left\{\frac{{s}+\mathrm{1}}{\left({s}−\mathrm{8}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }\right\} \\ $$$$=\mathcal{L}^{−\mathrm{1}} \left\{\frac{{s}−\mathrm{8}}{\left({s}−\mathrm{8}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }+\frac{\mathrm{9}}{\left({s}−\mathrm{8}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }\right\} \\ $$$$=\mathrm{cos}\left(\mathrm{6}\left({s}−\mathrm{8}\right)\right)+\frac{\mathrm{9}}{\mathrm{6}}\mathrm{sin}\left(\mathrm{6}\left({s}−\mathrm{8}\right)\right) \\ $$

Commented by Ar Brandon last updated on 10/Aug/21

You deleted your previous post.

$$\mathrm{You}\:\mathrm{deleted}\:\mathrm{your}\:\mathrm{previous}\:\mathrm{post}. \\ $$

Commented by mathdanisur last updated on 10/Aug/21

Cool Ser, Thank You

$$\mathrm{Cool}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{Thank}\:\mathrm{You} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com