Question Number 150263 by dany last updated on 10/Aug/21
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
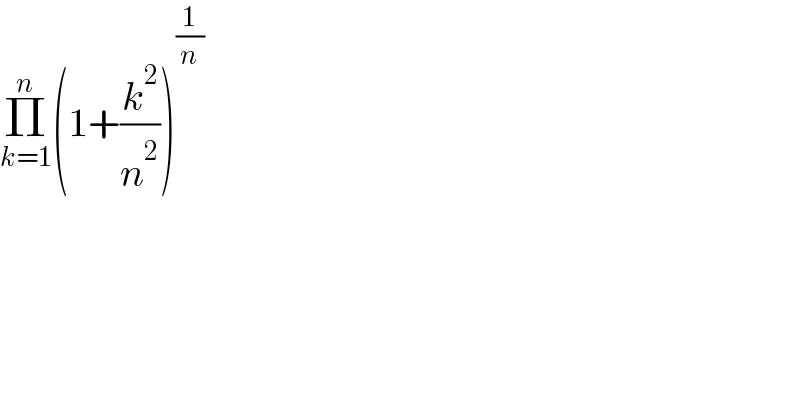
Commented by puissant last updated on 10/Aug/21
$$\mathrm{limite}? \\ $$
Commented by dany last updated on 10/Aug/21
$${yes} \\ $$
Answered by puissant last updated on 11/Aug/21
![U_n =Π_(k=1) ^n (1+(k^2 /n^2 ))^(1/n) let V_n =ln(U_n ) lim_(n→+∞) V_n =lim_(n→+∞) (1/n)Σ_(k=1) ^n ln(1+((k/n))^2 ) (Riemann integral ((b−a)/n)Σ_(k=1) ^n f(a+k((b−a)/n))) we have lim_(n→+∞) V_n = ∫_0 ^1 ln(1+x^2 )dx K=∫_0 ^1 ln(1+x^2 )dx { ((u=ln(1+x^2 ))),((v′=1)) :}⇒ { ((u′=((2x)/(1+x^2 )))),((v=x)) :} K=[xln(1+x^2 )]_0 ^1 −2∫_0 ^1 (x^2 /(1+x^2 ))dx =ln2−2∫_0 ^1 ((x^2 +1)/(x^2 +1))dx+2∫_0 ^1 (1/(1+x^2 ))dx =ln2−2[x]_0 ^1 +2[arctan(x)]_0 ^1 =ln2−2+(π/2).. lim_(n→+∞) V_n =lim_(n→+∞) ln(U_n ) ⇒ lim_(n→+∞) U_n = e^(lim_(n→+∞) V_n ) ⇒ lim_(n→+∞) U_n = e^(ln2−2+(π/2)) lim_(n→+∞) Π_(k=1) ^n (1+(k^2 /n^2 ))^(1/n) = 2e^((π/2)−2) .. ...........Le puissant...........](Q150269.png)
$$\mathrm{U}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \mathrm{let}\:\mathrm{V}_{\mathrm{n}} =\mathrm{ln}\left(\mathrm{U}_{\mathrm{n}} \right) \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{V}_{\mathrm{n}} =\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} \right) \\ $$$$\left(\mathrm{Riemann}\:\mathrm{integral}\:\frac{\mathrm{b}−\mathrm{a}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{f}\left(\mathrm{a}+\mathrm{k}\frac{\mathrm{b}−\mathrm{a}}{\mathrm{n}}\right)\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{V}_{\mathrm{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\mathrm{K}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\begin{cases}{\mathrm{u}=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\\{\mathrm{v}'=\mathrm{1}}\end{cases}\Rightarrow\:\begin{cases}{\mathrm{u}'=\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\\{\mathrm{v}=\mathrm{x}}\end{cases} \\ $$$$\mathrm{K}=\left[\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{ln2}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{ln2}−\mathrm{2}\left[\mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2}\left[\mathrm{arctan}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{ln2}−\mathrm{2}+\frac{\pi}{\mathrm{2}}.. \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{V}_{\mathrm{n}} =\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{U}_{\mathrm{n}} \right) \\ $$$$\Rightarrow\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{U}_{\mathrm{n}} =\:\mathrm{e}^{\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{V}_{\mathrm{n}} } \\ $$$$\Rightarrow\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{U}_{\mathrm{n}} =\:\mathrm{e}^{\mathrm{ln2}−\mathrm{2}+\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\:\mathrm{2e}^{\frac{\pi}{\mathrm{2}}−\mathrm{2}} .. \\ $$$$ \\ $$$$\:\:...........\mathrm{Le}\:\mathrm{puissant}........... \\ $$
Answered by Ar Brandon last updated on 10/Aug/21
![L=lim_(n→∞) Π_(k=1) ^n (1+(k^2 /n^2 ))^(1/n) lnL=lim_(n→∞) (1/n)lnΠ_(k=1) ^n (1+(k^2 /n^2 ))=lim_(n→∞) (1/n)Σ_(k=1) ^n ln(1+(k^2 /n^2 )) =∫_0 ^1 ln(1+x^2 )dx=[xln(1+x^2 )]_0 ^1 −2∫_0 ^1 (x^2 /(1+x^2 ))dx =ln2−2∫_0 ^1 (1−(1/(1+x^2 )))dx=ln2−2+(π/2) L=e^(ln2−2+(π/2)) =2e^((π/2)−2)](Q150268.png)
$$\mathscr{L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\mathrm{ln}\mathscr{L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\mathrm{ln}\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}=\left[{x}\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{ln2}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}=\mathrm{ln2}−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathscr{L}={e}^{\mathrm{ln2}−\mathrm{2}+\frac{\pi}{\mathrm{2}}} =\mathrm{2}{e}^{\frac{\pi}{\mathrm{2}}−\mathrm{2}} \\ $$