Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 15036 by Tinkutara last updated on 07/Jun/17

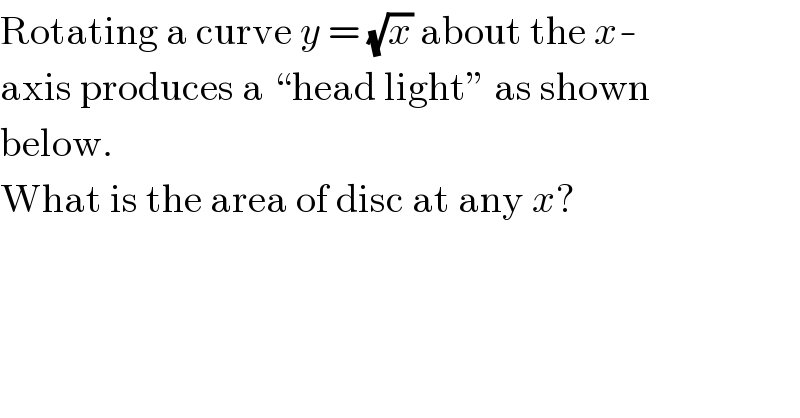
Rotating a curve y = (√x) about the x- axis produces a “head light” as shown below. What is the area of disc at any x?

$$\mathrm{Rotating}\:\mathrm{a}\:\mathrm{curve}\:{y}\:=\:\sqrt{{x}}\:\mathrm{about}\:\mathrm{the}\:{x}- \\ $$$$\mathrm{axis}\:\mathrm{produces}\:\mathrm{a}\:``\mathrm{head}\:\mathrm{light}''\:\mathrm{as}\:\mathrm{shown} \\ $$$$\mathrm{below}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{disc}\:\mathrm{at}\:\mathrm{any}\:{x}? \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Commented by Tinkutara last updated on 07/Jun/17

In the above problem what is the volume of this head light where x varies from 0 to 2?

$$\mathrm{In}\:\mathrm{the}\:\mathrm{above}\:\mathrm{problem}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{volume}\:\mathrm{of}\:\mathrm{this}\:\mathrm{head}\:\mathrm{light}\:\mathrm{where}\:{x}\:\mathrm{varies} \\ $$$$\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:\mathrm{2}? \\ $$

Answered by ajfour last updated on 07/Jun/17

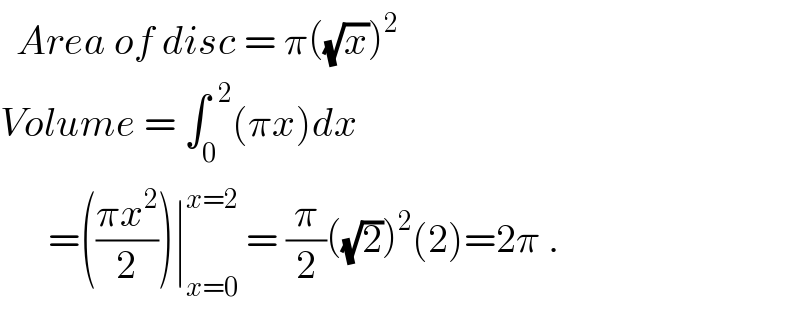
Area of disc = π((√x))^2 Volume = ∫_0 ^( 2) (πx)dx =(((πx^2 )/2))∣_(x=0) ^(x=2) = (π/2)((√2))^2 (2)=2π .

$$\:\:{Area}\:{of}\:{disc}\:=\:\pi\left(\sqrt{{x}}\right)^{\mathrm{2}} \: \\ $$$${Volume}\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{2}} \left(\pi{x}\right){dx} \\ $$$$\:\:\:\:\:\:=\left(\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid_{{x}=\mathrm{0}} ^{{x}=\mathrm{2}} \:=\:\frac{\pi}{\mathrm{2}}\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2}\right)=\mathrm{2}\pi\:. \\ $$

Commented by Tinkutara last updated on 07/Jun/17

But will the disc be circular so that we can apply area = πr^2 or will they be elliptical?

$$\mathrm{But}\:\mathrm{will}\:\mathrm{the}\:\mathrm{disc}\:\mathrm{be}\:\mathrm{circular}\:\mathrm{so}\:\mathrm{that}\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{apply}\:\mathrm{area}\:=\:\pi{r}^{\mathrm{2}} \:\mathrm{or}\:\mathrm{will}\:\mathrm{they}\:\mathrm{be} \\ $$$$\mathrm{elliptical}? \\ $$

Commented by ajfour last updated on 07/Jun/17

an elementary layer of disc of at location t has its thickness dt and radius (√t) . Its volume will be dV=(Area×thickness) = π((√t))^2 dt to obtain the sum of volumes of such consecutive layers starting at t=0 till t=x , we integrate the expression of dV with limits t=0, to t=x . V (x)=π((t^2 /2))∣_(t=0) ^(t=x) =((πx^2 )/2) .

$${an}\:{elementary}\:{layer}\:{of}\:{disc}\:{of} \\ $$$${at}\:{location}\:{t}\:{has}\:{its}\:{thickness}\:{dt} \\ $$$${and}\:{radius}\:\sqrt{{t}}\:.\:{Its}\:{volume}\:{will}\:{be} \\ $$$${dV}=\left({Area}×{thickness}\right) \\ $$$$\:\:\:\:\:=\:\pi\left(\sqrt{{t}}\right)^{\mathrm{2}} {dt} \\ $$$${to}\:{obtain}\:{the}\:\:{sum}\:{of}\:{volumes} \\ $$$${of}\:{such}\:{consecutive}\:{layers}\:{starting} \\ $$$${at}\:{t}=\mathrm{0}\:{till}\:{t}={x}\:,\:{we}\:{integrate}\:{the} \\ $$$${expression}\:{of}\:{dV}\:\:{with}\:{limits} \\ $$$${t}=\mathrm{0},\:{to}\:\:{t}={x}\:. \\ $$$${V}\:\left({x}\right)=\pi\left(\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right)\mid_{{t}=\mathrm{0}} ^{{t}={x}} \:=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}}\:. \\ $$

Commented by ajfour last updated on 07/Jun/17

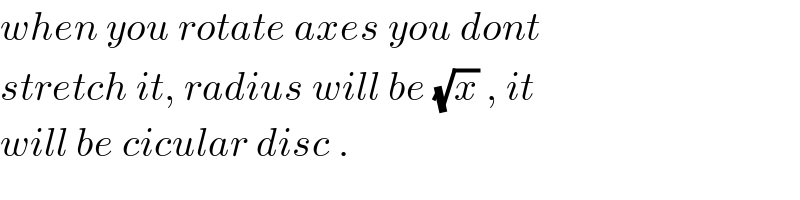
when you rotate axes you dont stretch it, radius will be (√x) , it will be cicular disc .

$${when}\:{you}\:{rotate}\:{axes}\:{you}\:{dont} \\ $$$${stretch}\:{it},\:{radius}\:{will}\:{be}\:\sqrt{{x}}\:,\:{it} \\ $$$${will}\:{be}\:{cicular}\:{disc}\:. \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com