Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 150363 by ajfour last updated on 11/Aug/21

Commented by ajfour last updated on 11/Aug/21

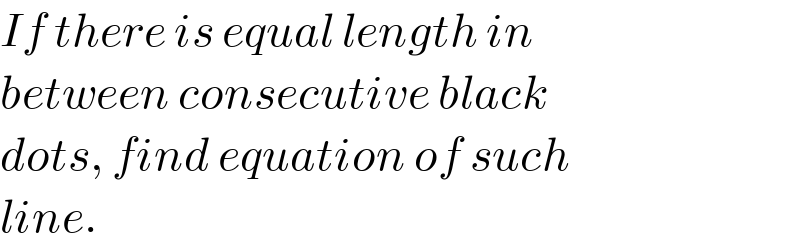
If there is equal length in between consecutive black dots, find equation of such line.

$${If}\:{there}\:{is}\:{equal}\:{length}\:{in} \\ $$$${between}\:{consecutive}\:{black} \\ $$$${dots},\:{find}\:{equation}\:{of}\:{such} \\ $$$${line}. \\ $$

Commented by mr W last updated on 11/Aug/21

it′s possible and the right most point lies always on the x−axis.

$${it}'{s}\:{possible}\:{and}\:{the}\:{right}\:{most}\:{point} \\ $$$${lies}\:{always}\:{on}\:{the}\:{x}−{axis}. \\ $$

Commented by mr W last updated on 11/Aug/21

Commented by mr W last updated on 11/Aug/21

Commented by mr W last updated on 11/Aug/21

Answered by mr W last updated on 12/Aug/21

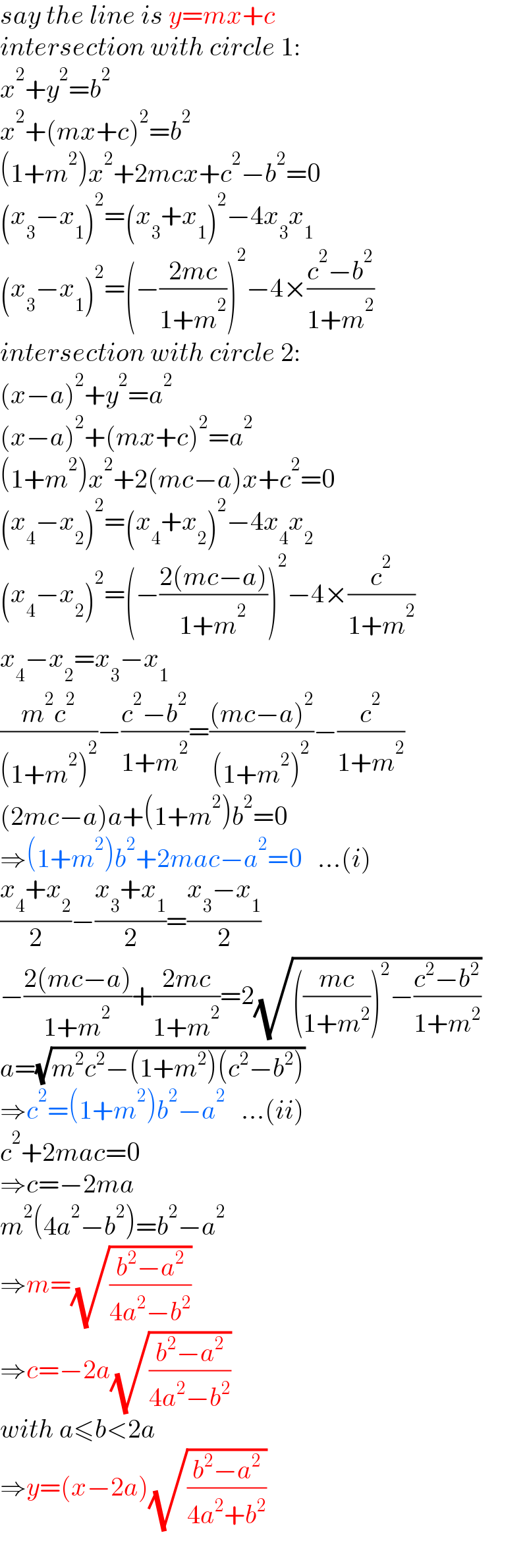
say the line is y=mx+c intersection with circle 1: x^2 +y^2 =b^2 x^2 +(mx+c)^2 =b^2 (1+m^2 )x^2 +2mcx+c^2 −b^2 =0 (x_3 −x_1 )^2 =(x_3 +x_1 )^2 −4x_3 x_1 (x_3 −x_1 )^2 =(−((2mc)/(1+m^2 )))^2 −4×((c^2 −b^2 )/(1+m^2 )) intersection with circle 2: (x−a)^2 +y^2 =a^2 (x−a)^2 +(mx+c)^2 =a^2 (1+m^2 )x^2 +2(mc−a)x+c^2 =0 (x_4 −x_2 )^2 =(x_4 +x_2 )^2 −4x_4 x_2 (x_4 −x_2 )^2 =(−((2(mc−a))/(1+m^2 )))^2 −4×(c^2 /(1+m^2 )) x_4 −x_2 =x_3 −x_1 ((m^2 c^2 )/((1+m^2 )^2 ))−((c^2 −b^2 )/(1+m^2 ))=(((mc−a)^2 )/((1+m^2 )^2 ))−(c^2 /(1+m^2 )) (2mc−a)a+(1+m^2 )b^2 =0 ⇒(1+m^2 )b^2 +2mac−a^2 =0 ...(i) ((x_4 +x_2 )/2)−((x_3 +x_1 )/2)=((x_3 −x_1 )/2) −((2(mc−a))/(1+m^2 ))+((2mc)/(1+m^2 ))=2(√((((mc)/(1+m^2 )))^2 −((c^2 −b^2 )/(1+m^2 )))) a=(√(m^2 c^2 −(1+m^2 )(c^2 −b^2 ))) ⇒c^2 =(1+m^2 )b^2 −a^2 ...(ii) c^2 +2mac=0 ⇒c=−2ma m^2 (4a^2 −b^2 )=b^2 −a^2 ⇒m=(√((b^2 −a^2 )/(4a^2 −b^2 ))) ⇒c=−2a(√((b^2 −a^2 )/(4a^2 −b^2 ))) with a≤b<2a ⇒y=(x−2a)(√((b^2 −a^2 )/(4a^2 +b^2 )))

$${say}\:{the}\:{line}\:{is}\:{y}={mx}+{c} \\ $$$${intersection}\:{with}\:{circle}\:\mathrm{1}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left({mx}+{c}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}{mcx}+{c}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}_{\mathrm{3}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{3}} +{x}_{\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{3}} {x}_{\mathrm{1}} \\ $$$$\left({x}_{\mathrm{3}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} =\left(−\frac{\mathrm{2}{mc}}{\mathrm{1}+{m}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{4}×\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${intersection}\:{with}\:{circle}\:\mathrm{2}: \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +\left({mx}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}\left({mc}−{a}\right){x}+{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}_{\mathrm{4}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{4}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{4}} {x}_{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{4}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} =\left(−\frac{\mathrm{2}\left({mc}−{a}\right)}{\mathrm{1}+{m}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{4}×\frac{{c}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${x}_{\mathrm{4}} −{x}_{\mathrm{2}} ={x}_{\mathrm{3}} −{x}_{\mathrm{1}} \\ $$$$\frac{{m}^{\mathrm{2}} {c}^{\mathrm{2}} }{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} }=\frac{\left({mc}−{a}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} }−\frac{{c}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}{mc}−{a}\right){a}+\left(\mathrm{1}+{m}^{\mathrm{2}} \right){b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{m}^{\mathrm{2}} \right){b}^{\mathrm{2}} +\mathrm{2}{mac}−{a}^{\mathrm{2}} =\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\frac{{x}_{\mathrm{4}} +{x}_{\mathrm{2}} }{\mathrm{2}}−\frac{{x}_{\mathrm{3}} +{x}_{\mathrm{1}} }{\mathrm{2}}=\frac{{x}_{\mathrm{3}} −{x}_{\mathrm{1}} }{\mathrm{2}} \\ $$$$−\frac{\mathrm{2}\left({mc}−{a}\right)}{\mathrm{1}+{m}^{\mathrm{2}} }+\frac{\mathrm{2}{mc}}{\mathrm{1}+{m}^{\mathrm{2}} }=\mathrm{2}\sqrt{\left(\frac{{mc}}{\mathrm{1}+{m}^{\mathrm{2}} }\right)^{\mathrm{2}} −\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} }} \\ $$$${a}=\sqrt{{m}^{\mathrm{2}} {c}^{\mathrm{2}} −\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow{c}^{\mathrm{2}} =\left(\mathrm{1}+{m}^{\mathrm{2}} \right){b}^{\mathrm{2}} −{a}^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$${c}^{\mathrm{2}} +\mathrm{2}{mac}=\mathrm{0}\: \\ $$$$\Rightarrow{c}=−\mathrm{2}{ma} \\ $$$${m}^{\mathrm{2}} \left(\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)={b}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\Rightarrow{m}=\sqrt{\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$$$\Rightarrow{c}=−\mathrm{2}{a}\sqrt{\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$$${with}\:{a}\leqslant{b}<\mathrm{2}{a} \\ $$$$\Rightarrow{y}=\left({x}−\mathrm{2}{a}\right)\sqrt{\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$

Commented by ajfour last updated on 12/Aug/21

Thank you sir, i followed it all.

Answered by ajfour last updated on 12/Aug/21

Commented by ajfour last updated on 12/Aug/21

For a=4, b=5 such a vertical line is x=(9/2)−((√(274))/4) ≈ 0.36176 (green vertical)

$${For}\:{a}=\mathrm{4},\:{b}=\mathrm{5} \\ $$$${such}\:{a}\:{vertical}\:{line}\:{is} \\ $$$$\:\:{x}=\frac{\mathrm{9}}{\mathrm{2}}−\frac{\sqrt{\mathrm{274}}}{\mathrm{4}}\:\:\approx\:\mathrm{0}.\mathrm{36176} \\ $$$$\:\:\left({green}\:{vertical}\right) \\ $$

Commented by ajfour last updated on 12/Aug/21

Commented by ajfour last updated on 12/Aug/21

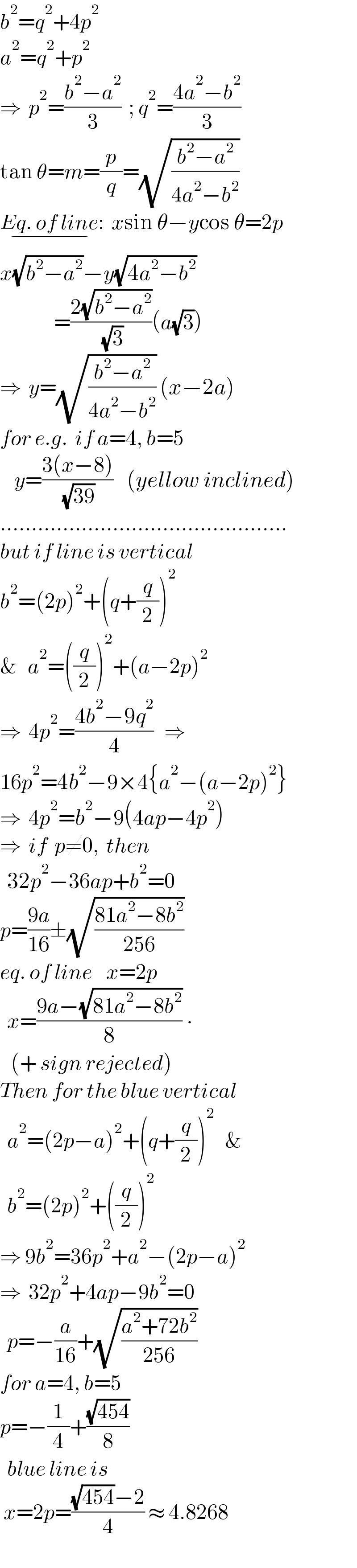
b^2 =q^2 +4p^2 a^2 =q^2 +p^2 ⇒ p^2 =((b^2 −a^2 )/3) ; q^2 =((4a^2 −b^2 )/3) tan θ=m=(p/q)=(√((b^2 −a^2 )/(4a^2 −b^2 ))) Eq. of line_(−) : xsin θ−ycos θ=2p x(√(b^2 −a^2 ))−y(√(4a^2 −b^2 )) =((2(√(b^2 −a^2 )))/( (√3)))(a(√3)) ⇒ y=(√((b^2 −a^2 )/(4a^2 −b^2 ))) (x−2a) for e.g. if a=4, b=5 y=((3(x−8))/( (√(39)))) (yellow inclined) .............................................. but if line is vertical b^2 =(2p)^2 +(q+(q/2))^2 & a^2 =((q/2))^2 +(a−2p)^2 ⇒ 4p^2 =((4b^2 −9q^2 )/4) ⇒ 16p^2 =4b^2 −9×4{a^2 −(a−2p)^2 } ⇒ 4p^2 =b^2 −9(4ap−4p^2 ) ⇒ if p≠0, then 32p^2 −36ap+b^2 =0 p=((9a)/(16))±(√((81a^2 −8b^2 )/(256))) eq. of line x=2p x=((9a−(√(81a^2 −8b^2 )))/8) ∙ (+ sign rejected) Then for the blue vertical a^2 =(2p−a)^2 +(q+(q/2))^2 & b^2 =(2p)^2 +((q/2))^2 ⇒ 9b^2 =36p^2 +a^2 −(2p−a)^2 ⇒ 32p^2 +4ap−9b^2 =0 p=−(a/(16))+(√((a^2 +72b^2 )/(256))) for a=4, b=5 p=−(1/4)+((√(454))/8) blue line is x=2p=(((√(454))−2)/4) ≈ 4.8268

$${b}^{\mathrm{2}} ={q}^{\mathrm{2}} +\mathrm{4}{p}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} ={q}^{\mathrm{2}} +{p}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{3}}\:\:;\:{q}^{\mathrm{2}} =\frac{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\mathrm{tan}\:\theta={m}=\frac{{p}}{{q}}=\sqrt{\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$$$\underset{−} {{Eq}.\:{of}\:{line}}:\:\:{x}\mathrm{sin}\:\theta−{y}\mathrm{cos}\:\theta=\mathrm{2}{p} \\ $$$${x}\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }−{y}\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\sqrt{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\:\sqrt{\mathrm{3}}}\left({a}\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow\:\:{y}=\sqrt{\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\:\left({x}−\mathrm{2}{a}\right) \\ $$$${for}\:{e}.{g}.\:\:{if}\:{a}=\mathrm{4},\:{b}=\mathrm{5} \\ $$$$\:\:\:\:{y}=\frac{\mathrm{3}\left({x}−\mathrm{8}\right)}{\:\sqrt{\mathrm{39}}}\:\:\:\left({yellow}\:{inclined}\right) \\ $$$$.............................................. \\ $$$${but}\:{if}\:{line}\:{is}\:{vertical} \\ $$$${b}^{\mathrm{2}} =\left(\mathrm{2}{p}\right)^{\mathrm{2}} +\left({q}+\frac{{q}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\&\:\:\:{a}^{\mathrm{2}} =\left(\frac{{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({a}−\mathrm{2}{p}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{4}{p}^{\mathrm{2}} =\frac{\mathrm{4}{b}^{\mathrm{2}} −\mathrm{9}{q}^{\mathrm{2}} }{\mathrm{4}}\:\:\:\Rightarrow \\ $$$$\mathrm{16}{p}^{\mathrm{2}} =\mathrm{4}{b}^{\mathrm{2}} −\mathrm{9}×\mathrm{4}\left\{{a}^{\mathrm{2}} −\left({a}−\mathrm{2}{p}\right)^{\mathrm{2}} \right\} \\ $$$$\Rightarrow\:\:\mathrm{4}{p}^{\mathrm{2}} ={b}^{\mathrm{2}} −\mathrm{9}\left(\mathrm{4}{ap}−\mathrm{4}{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{if}\:\:{p}\neq\mathrm{0},\:\:{then} \\ $$$$\:\:\mathrm{32}{p}^{\mathrm{2}} −\mathrm{36}{ap}+{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}=\frac{\mathrm{9}{a}}{\mathrm{16}}\pm\sqrt{\frac{\mathrm{81}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} }{\mathrm{256}}} \\ $$$${eq}.\:{of}\:{line}\:\:\:\:{x}=\mathrm{2}{p} \\ $$$$\:\:{x}=\frac{\mathrm{9}{a}−\sqrt{\mathrm{81}{a}^{\mathrm{2}} −\mathrm{8}{b}^{\mathrm{2}} }}{\mathrm{8}}\:\centerdot \\ $$$$\:\:\:\left(+\:{sign}\:{rejected}\right) \\ $$$${Then}\:{for}\:{the}\:{blue}\:{vertical} \\ $$$$\:\:{a}^{\mathrm{2}} =\left(\mathrm{2}{p}−{a}\right)^{\mathrm{2}} +\left({q}+\frac{{q}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:\& \\ $$$$\:\:{b}^{\mathrm{2}} =\left(\mathrm{2}{p}\right)^{\mathrm{2}} +\left(\frac{{q}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{9}{b}^{\mathrm{2}} =\mathrm{36}{p}^{\mathrm{2}} +{a}^{\mathrm{2}} −\left(\mathrm{2}{p}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{32}{p}^{\mathrm{2}} +\mathrm{4}{ap}−\mathrm{9}{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:{p}=−\frac{{a}}{\mathrm{16}}+\sqrt{\frac{{a}^{\mathrm{2}} +\mathrm{72}{b}^{\mathrm{2}} }{\mathrm{256}}} \\ $$$${for}\:{a}=\mathrm{4},\:{b}=\mathrm{5} \\ $$$${p}=−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\sqrt{\mathrm{454}}}{\mathrm{8}} \\ $$$$\:\:{blue}\:{line}\:{is}\: \\ $$$$\:{x}=\mathrm{2}{p}=\frac{\sqrt{\mathrm{454}}−\mathrm{2}}{\mathrm{4}}\:\approx\:\mathrm{4}.\mathrm{8268} \\ $$$$ \\ $$

Commented by mr W last updated on 13/Aug/21

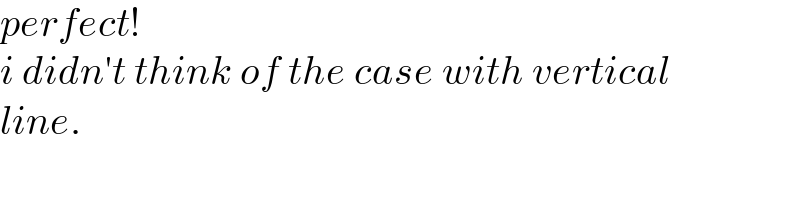
perfect! i didn′t think of the case with vertical line.

$${perfect}! \\ $$$${i}\:{didn}'{t}\:{think}\:{of}\:{the}\:{case}\:{with}\:{vertical} \\ $$$${line}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com