Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 15039 by Tinkutara last updated on 07/Jun/17

The acceleration of an object is given by a(t) = cos(πt) ms^(−2) and its velocity at time t = 0 is (1/(2π)) m/s at origin. Its velocity at t = (3/2) s is? The object′s position at t = (3/2) s is?

$$\mathrm{The}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{an}\:\mathrm{object}\:\mathrm{is}\:\mathrm{given} \\ $$$$\mathrm{by}\:{a}\left({t}\right)\:=\:\mathrm{cos}\left(\pi{t}\right)\:\mathrm{ms}^{−\mathrm{2}} \:\mathrm{and}\:\mathrm{its}\:\mathrm{velocity} \\ $$$$\mathrm{at}\:\mathrm{time}\:{t}\:=\:\mathrm{0}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}\pi}\:\mathrm{m}/\mathrm{s}\:\mathrm{at}\:\mathrm{origin}.\:\mathrm{Its} \\ $$$$\mathrm{velocity}\:\mathrm{at}\:{t}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{s}\:\mathrm{is}? \\ $$$$\mathrm{The}\:\mathrm{object}'\mathrm{s}\:\mathrm{position}\:\mathrm{at}\:{t}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{s}\:\mathrm{is}? \\ $$

Answered by ajfour last updated on 07/Jun/17

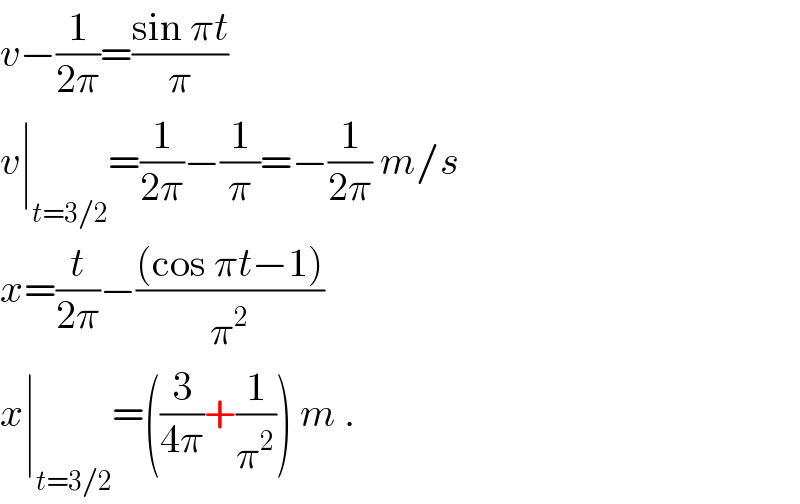
v−(1/(2π))=((sin πt)/π) v∣_(t=3/2) =(1/(2π))−(1/π)=−(1/(2π)) m/s x=(t/(2π))−(((cos πt−1))/π^2 ) x∣_(t=3/2) =((3/(4π))+(1/π^2 )) m .

$${v}−\frac{\mathrm{1}}{\mathrm{2}\pi}=\frac{\mathrm{sin}\:\pi{t}}{\pi} \\ $$$${v}\mid_{{t}=\mathrm{3}/\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}\pi}−\frac{\mathrm{1}}{\pi}=−\frac{\mathrm{1}}{\mathrm{2}\pi}\:{m}/{s} \\ $$$${x}=\frac{{t}}{\mathrm{2}\pi}−\frac{\left(\mathrm{cos}\:\pi{t}−\mathrm{1}\right)}{\pi^{\mathrm{2}} } \\ $$$${x}\mid_{{t}=\mathrm{3}/\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{4}\pi}+\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\right)\:{m}\:. \\ $$

Commented by Tinkutara last updated on 07/Jun/17

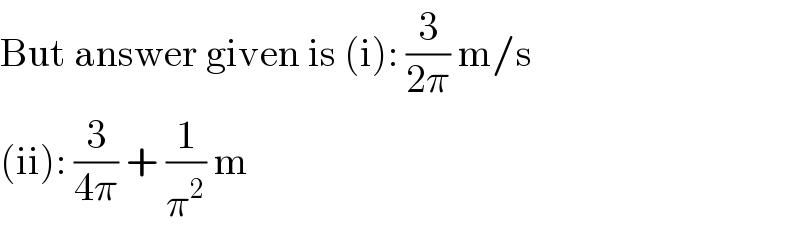
But answer given is (i): (3/(2π)) m/s (ii): (3/(4π)) + (1/π^2 ) m

$$\mathrm{But}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{is}\:\left(\mathrm{i}\right):\:\frac{\mathrm{3}}{\mathrm{2}\pi}\:\mathrm{m}/\mathrm{s} \\ $$$$\left(\mathrm{ii}\right):\:\frac{\mathrm{3}}{\mathrm{4}\pi}\:+\:\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\:\mathrm{m} \\ $$

Commented by mrW1 last updated on 07/Jun/17

the answer given in your book is wrong.

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{in}\:\mathrm{your}\:\mathrm{book}\:\mathrm{is}\:\mathrm{wrong}. \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by mrW1 last updated on 07/Jun/17

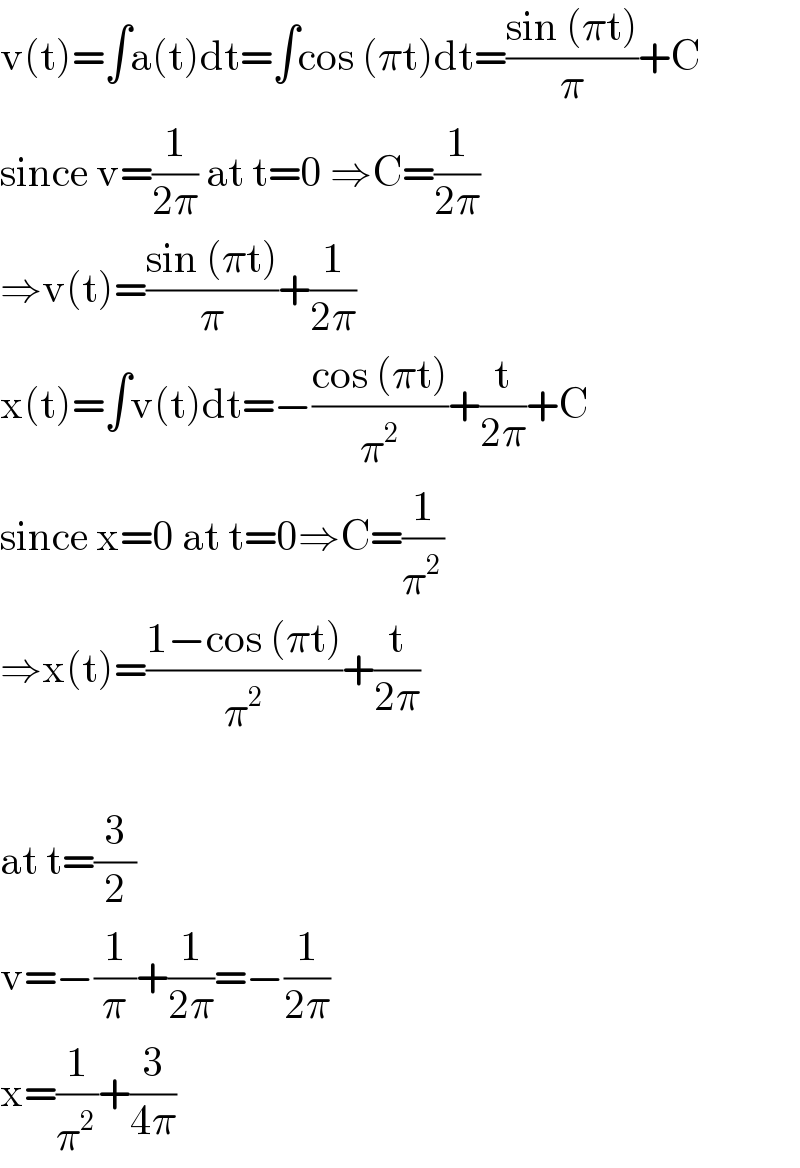
v(t)=∫a(t)dt=∫cos (πt)dt=((sin (πt))/π)+C since v=(1/(2π)) at t=0 ⇒C=(1/(2π)) ⇒v(t)=((sin (πt))/π)+(1/(2π)) x(t)=∫v(t)dt=−((cos (πt))/π^2 )+(t/(2π))+C since x=0 at t=0⇒C=(1/π^2 ) ⇒x(t)=((1−cos (πt))/π^2 )+(t/(2π)) at t=(3/2) v=−(1/π)+(1/(2π))=−(1/(2π)) x=(1/π^2 )+(3/(4π))

$$\mathrm{v}\left(\mathrm{t}\right)=\int\mathrm{a}\left(\mathrm{t}\right)\mathrm{dt}=\int\mathrm{cos}\:\left(\pi\mathrm{t}\right)\mathrm{dt}=\frac{\mathrm{sin}\:\left(\pi\mathrm{t}\right)}{\pi}+\mathrm{C} \\ $$$$\mathrm{since}\:\mathrm{v}=\frac{\mathrm{1}}{\mathrm{2}\pi}\:\mathrm{at}\:\mathrm{t}=\mathrm{0}\:\Rightarrow\mathrm{C}=\frac{\mathrm{1}}{\mathrm{2}\pi} \\ $$$$\Rightarrow\mathrm{v}\left(\mathrm{t}\right)=\frac{\mathrm{sin}\:\left(\pi\mathrm{t}\right)}{\pi}+\frac{\mathrm{1}}{\mathrm{2}\pi} \\ $$$$\mathrm{x}\left(\mathrm{t}\right)=\int\mathrm{v}\left(\mathrm{t}\right)\mathrm{dt}=−\frac{\mathrm{cos}\:\left(\pi\mathrm{t}\right)}{\pi^{\mathrm{2}} }+\frac{\mathrm{t}}{\mathrm{2}\pi}+\mathrm{C} \\ $$$$\mathrm{since}\:\mathrm{x}=\mathrm{0}\:\mathrm{at}\:\mathrm{t}=\mathrm{0}\Rightarrow\mathrm{C}=\frac{\mathrm{1}}{\pi^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{t}\right)=\frac{\mathrm{1}−\mathrm{cos}\:\left(\pi\mathrm{t}\right)}{\pi^{\mathrm{2}} }+\frac{\mathrm{t}}{\mathrm{2}\pi} \\ $$$$ \\ $$$$\mathrm{at}\:\mathrm{t}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{v}=−\frac{\mathrm{1}}{\pi}+\frac{\mathrm{1}}{\mathrm{2}\pi}=−\frac{\mathrm{1}}{\mathrm{2}\pi} \\ $$$$\mathrm{x}=\frac{\mathrm{1}}{\pi^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}\pi} \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com