Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 150429 by ZiYangLee last updated on 12/Aug/21

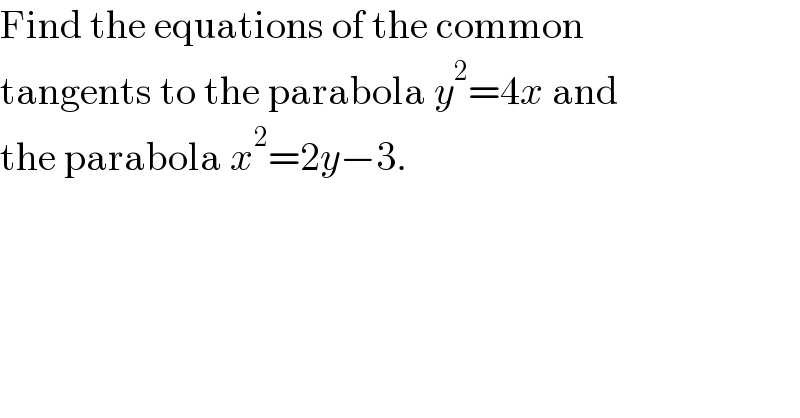
Find the equations of the common tangents to the parabola y^2 =4x and the parabola x^2 =2y−3.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{the}\:\mathrm{common} \\ $$$$\mathrm{tangents}\:\mathrm{to}\:\mathrm{the}\:\mathrm{parabola}\:{y}^{\mathrm{2}} =\mathrm{4}{x}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{parabola}\:{x}^{\mathrm{2}} =\mathrm{2}{y}−\mathrm{3}. \\ $$

Answered by Olaf_Thorendsen last updated on 12/Aug/21

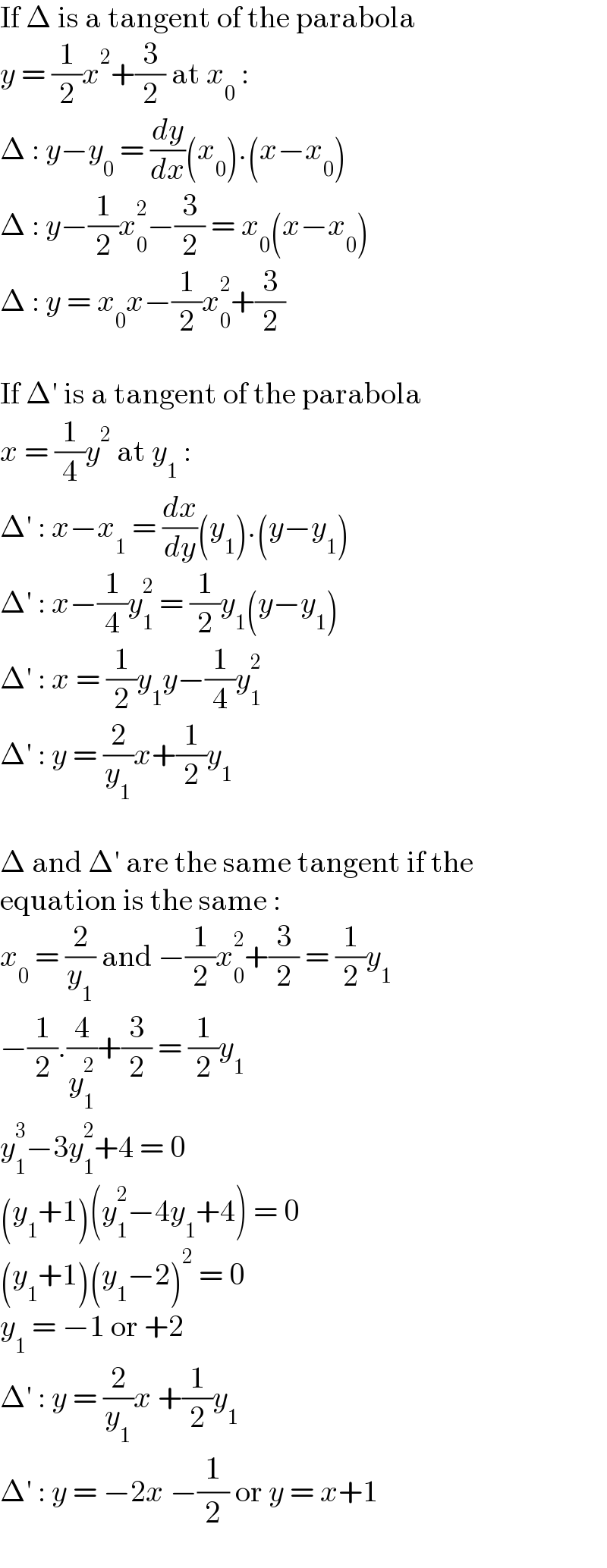
If Δ is a tangent of the parabola y = (1/2)x^2 +(3/2) at x_0 : Δ : y−y_0 = (dy/dx)(x_0 ).(x−x_0 ) Δ : y−(1/2)x_0 ^2 −(3/2) = x_0 (x−x_0 ) Δ : y = x_0 x−(1/2)x_0 ^2 +(3/2) If Δ′ is a tangent of the parabola x = (1/4)y^2 at y_1 : Δ′ : x−x_1 = (dx/dy)(y_1 ).(y−y_1 ) Δ′ : x−(1/4)y_1 ^2 = (1/2)y_1 (y−y_1 ) Δ′ : x = (1/2)y_1 y−(1/4)y_1 ^2 Δ′ : y = (2/y_1 )x+(1/2)y_1 Δ and Δ′ are the same tangent if the equation is the same : x_0 = (2/y_1 ) and −(1/2)x_0 ^2 +(3/2) = (1/2)y_1 −(1/2).(4/y_1 ^2 )+(3/2) = (1/2)y_1 y_1 ^3 −3y_1 ^2 +4 = 0 (y_1 +1)(y_1 ^2 −4y_1 +4) = 0 (y_1 +1)(y_1 −2)^2 = 0 y_1 = −1 or +2 Δ′ : y = (2/y_1 )x +(1/2)y_1 Δ′ : y = −2x −(1/2) or y = x+1

$$\mathrm{If}\:\Delta\:\mathrm{is}\:\mathrm{a}\:\mathrm{tangent}\:\mathrm{of}\:\mathrm{the}\:\mathrm{parabola} \\ $$$${y}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{at}\:{x}_{\mathrm{0}} \:: \\ $$$$\Delta\::\:{y}−{y}_{\mathrm{0}} \:=\:\frac{{dy}}{{dx}}\left({x}_{\mathrm{0}} \right).\left({x}−{x}_{\mathrm{0}} \right) \\ $$$$\Delta\::\:{y}−\frac{\mathrm{1}}{\mathrm{2}}{x}_{\mathrm{0}} ^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\:=\:{x}_{\mathrm{0}} \left({x}−{x}_{\mathrm{0}} \right) \\ $$$$\Delta\::\:{y}\:=\:{x}_{\mathrm{0}} {x}−\frac{\mathrm{1}}{\mathrm{2}}{x}_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{If}\:\Delta'\:\mathrm{is}\:\mathrm{a}\:\mathrm{tangent}\:\mathrm{of}\:\mathrm{the}\:\mathrm{parabola} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} \:\mathrm{at}\:{y}_{\mathrm{1}} \:: \\ $$$$\Delta'\::\:{x}−{x}_{\mathrm{1}} \:=\:\frac{{dx}}{{dy}}\left({y}_{\mathrm{1}} \right).\left({y}−{y}_{\mathrm{1}} \right) \\ $$$$\Delta'\::\:{x}−\frac{\mathrm{1}}{\mathrm{4}}{y}_{\mathrm{1}} ^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}{y}_{\mathrm{1}} \left({y}−{y}_{\mathrm{1}} \right) \\ $$$$\Delta'\::\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{y}_{\mathrm{1}} {y}−\frac{\mathrm{1}}{\mathrm{4}}{y}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Delta'\::\:{y}\:=\:\frac{\mathrm{2}}{{y}_{\mathrm{1}} }{x}+\frac{\mathrm{1}}{\mathrm{2}}{y}_{\mathrm{1}} \\ $$$$ \\ $$$$\Delta\:\mathrm{and}\:\Delta'\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{tangent}\:\mathrm{if}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:: \\ $$$${x}_{\mathrm{0}} \:=\:\frac{\mathrm{2}}{{y}_{\mathrm{1}} }\:\mathrm{and}\:−\frac{\mathrm{1}}{\mathrm{2}}{x}_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{y}_{\mathrm{1}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{4}}{{y}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{y}_{\mathrm{1}} \\ $$$${y}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{3}{y}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}\:=\:\mathrm{0} \\ $$$$\left({y}_{\mathrm{1}} +\mathrm{1}\right)\left({y}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{4}{y}_{\mathrm{1}} +\mathrm{4}\right)\:=\:\mathrm{0} \\ $$$$\left({y}_{\mathrm{1}} +\mathrm{1}\right)\left({y}_{\mathrm{1}} −\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${y}_{\mathrm{1}} \:=\:−\mathrm{1}\:\mathrm{or}\:+\mathrm{2} \\ $$$$\Delta'\::\:{y}\:=\:\frac{\mathrm{2}}{{y}_{\mathrm{1}} }{x}\:+\frac{\mathrm{1}}{\mathrm{2}}{y}_{\mathrm{1}} \\ $$$$\Delta'\::\:{y}\:=\:−\mathrm{2}{x}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{or}\:{y}\:=\:{x}+\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com