
Question Number 150451 by ajfour last updated on 12/Aug/21

Commented by Ar Brandon last updated on 12/Aug/21

$$\mathrm{I}\:\mathrm{admire}\:\mathrm{your}\:\mathrm{posts}\:\mathrm{sir}.\:\mathrm{Sadly}\:\mathrm{I}\:\mathrm{have}\:\mathrm{very}\:\mathrm{little}\:\mathrm{knowledge} \\ $$$$\mathrm{on}\:\mathrm{geometry}.\:\mathrm{You}'\mathrm{re}\:\mathrm{so}\:\mathrm{advanced}.\:\mathrm{Hahaha}\:!\:\mathrm{I}\:\mathrm{hope}\:\mathrm{I}\:\mathrm{will}\:\mathrm{get} \\ $$$$\mathrm{there}\:\mathrm{someday}. \\ $$
Commented by ajfour last updated on 12/Aug/21

$${Find}\:{maximum}\:{of}\:{ratio}\:{of} \\ $$$${regular}\:{cone}\:{volume}\:{to}\:{sphere} \\ $$$${volume}. \\ $$
Answered by ajfour last updated on 12/Aug/21

Commented by ajfour last updated on 12/Aug/21
![x^2 +y^2 =r^2 O(0, r−p, ptan θ) q^2 =(r−p)^2 +p^2 tan^2 θ s−(p/(cos θ))=R r=scos θ tan φ=((ptan θ)/(2r−p)) ((sin (θ+φ))/s)=((sin (θ−φ))/R) λ=((((1/3)πr^2 h))/(((2/3)πR^3 )))=(((s^2 cos^2 θ)(ssin θ))/(2R^3 )) λ=(1/2)[((sin (θ+φ))/(sin (θ−φ))]^3 sin θcos^2 θ .....](Q150490.png)
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${O}\left(\mathrm{0},\:{r}−{p},\:{p}\mathrm{tan}\:\theta\right) \\ $$$${q}^{\mathrm{2}} =\left({r}−{p}\right)^{\mathrm{2}} +{p}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta \\ $$$${s}−\frac{{p}}{\mathrm{cos}\:\theta}={R} \\ $$$${r}={s}\mathrm{cos}\:\theta \\ $$$$\mathrm{tan}\:\phi=\frac{{p}\mathrm{tan}\:\theta}{\mathrm{2}{r}−{p}} \\ $$$$\frac{\mathrm{sin}\:\left(\theta+\phi\right)}{{s}}=\frac{\mathrm{sin}\:\left(\theta−\phi\right)}{{R}} \\ $$$$\lambda=\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}\pi{r}^{\mathrm{2}} {h}\right)}{\left(\frac{\mathrm{2}}{\mathrm{3}}\pi{R}^{\mathrm{3}} \right)}=\frac{\left({s}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)\left({s}\mathrm{sin}\:\theta\right)}{\mathrm{2}{R}^{\mathrm{3}} } \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{sin}\:\left(\theta+\phi\right)}{\mathrm{sin}\:\left(\theta−\phi\right.}\right]^{\mathrm{3}} \mathrm{sin}\:\theta\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$..... \\ $$
Answered by mr W last updated on 12/Aug/21

Commented by ajfour last updated on 12/Aug/21

$${excellent}!\:{Sir};\:{from}\:{beginning} \\ $$$${till}\:{answer};\:{thanks},\:{indebted}. \\ $$
Commented by ajfour last updated on 12/Aug/21

$${but}\:{top}\:{point}\:{of}\:{cone}\:{can}\:{be}\:{lower} \\ $$$${than}\:{that}\:{of}\:{sphere}!\:{sir}. \\ $$$${They}\:{might}\:{just}\:{touch}\:{at} \\ $$$${say}\:\mathrm{20}°\:{down}\:{the}\:{cone}\:{base} \\ $$$${circle}... \\ $$$$\left({see}\:{my}\:{ans}.\:{diagram}..\right) \\ $$
Commented by mr W last updated on 12/Aug/21
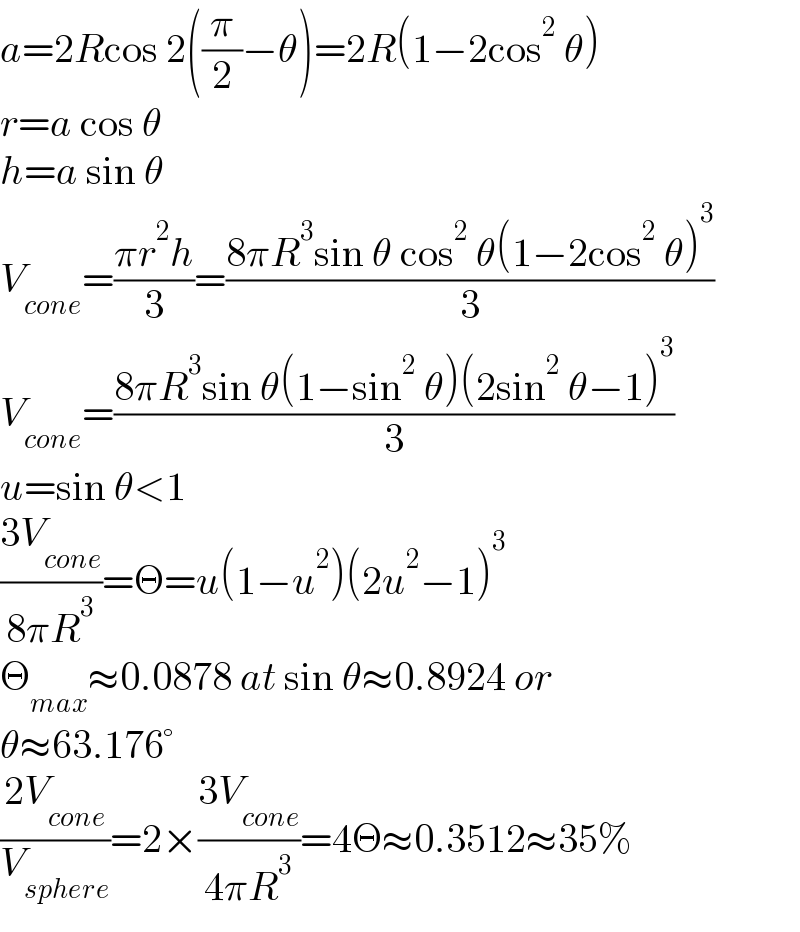
$${a}=\mathrm{2}{R}\mathrm{cos}\:\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\mathrm{2}{R}\left(\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \:\theta\right) \\ $$$${r}={a}\:\mathrm{cos}\:\theta \\ $$$${h}={a}\:\mathrm{sin}\:\theta \\ $$$${V}_{{cone}} =\frac{\pi{r}^{\mathrm{2}} {h}}{\mathrm{3}}=\frac{\mathrm{8}\pi{R}^{\mathrm{3}} \mathrm{sin}\:\theta\:\mathrm{cos}^{\mathrm{2}} \:\theta\left(\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \:\theta\right)^{\mathrm{3}} }{\mathrm{3}} \\ $$$${V}_{{cone}} =\frac{\mathrm{8}\pi{R}^{\mathrm{3}} \mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta\right)\left(\mathrm{2sin}^{\mathrm{2}} \:\theta−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}} \\ $$$${u}=\mathrm{sin}\:\theta<\mathrm{1} \\ $$$$\frac{\mathrm{3}{V}_{{cone}} }{\mathrm{8}\pi{R}^{\mathrm{3}} }=\Theta={u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\Theta_{{max}} \approx\mathrm{0}.\mathrm{0878}\:{at}\:\mathrm{sin}\:\theta\approx\mathrm{0}.\mathrm{8924}\:{or}\: \\ $$$$\theta\approx\mathrm{63}.\mathrm{176}° \\ $$$$\frac{\mathrm{2}{V}_{{cone}} }{{V}_{{sphere}} }=\mathrm{2}×\frac{\mathrm{3}{V}_{{cone}} }{\mathrm{4}\pi{R}^{\mathrm{3}} }=\mathrm{4}\Theta\approx\mathrm{0}.\mathrm{3512}\approx\mathrm{35\%} \\ $$
Commented by mr W last updated on 12/Aug/21

$${i}\:{understand}\:{from}\:{the}\:{first}\:{diagram} \\ $$$${that}\:{each}\:{cone}\:{should}\:{be}\:{inside}\:{a} \\ $$$${hemisphere}. \\ $$
