Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 150467 by saly last updated on 12/Aug/21

Commented by saly last updated on 12/Aug/21

Do you help me

$$\:\:{Do}\:{you}\:{help}\:{me} \\ $$

Answered by aleks041103 last updated on 13/Aug/21

=lim_(x→π/2) ((2xsin x−π)/(cos x))=[(0/0)] =^(L′Hopital) lim_(x→π/2) ((2xcos x+2sin x)/(−sinx))= =−((πcos(π/2)+2sin(π/2))/(sin(π/2)))= =−2

$$=\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{2}{x}\mathrm{sin}\:\:{x}−\pi}{\mathrm{cos}\:{x}}=\left[\frac{\mathrm{0}}{\mathrm{0}}\right] \\ $$$$\overset{{L}'{Hopital}} {=}\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{2}{x}\mathrm{cos}\:{x}+\mathrm{2sin}\:{x}}{−{sinx}}= \\ $$$$=−\frac{\pi{cos}\left(\pi/\mathrm{2}\right)+\mathrm{2}{sin}\left(\pi/\mathrm{2}\right)}{{sin}\left(\pi/\mathrm{2}\right)}= \\ $$$$=−\mathrm{2} \\ $$

Commented by saly last updated on 13/Aug/21

thank you very much

$$\:{thank}\:{you}\:{very}\:{much} \\ $$

Commented by EDWIN88 last updated on 13/Aug/21

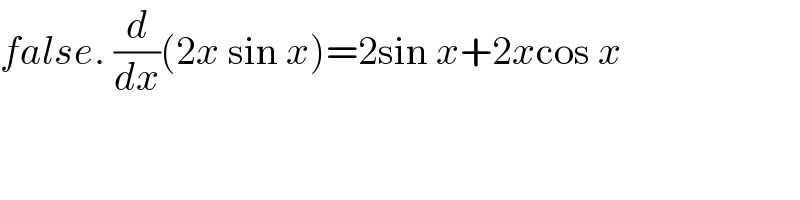
false. (d/dx)(2x sin x)=2sin x+2xcos x

$${false}.\:\frac{{d}}{{dx}}\left(\mathrm{2}{x}\:\mathrm{sin}\:{x}\right)=\mathrm{2sin}\:{x}+\mathrm{2}{x}\mathrm{cos}\:{x} \\ $$

Commented by aleks041103 last updated on 13/Aug/21

Yes, you′re right! I′ll correct it right now.

$${Yes},\:{you}'{re}\:{right}!\:{I}'{ll}\:{correct}\:{it}\:{right} \\ $$$${now}. \\ $$

Answered by liberty last updated on 13/Aug/21

lim_(x→(π/2)) (((2xsin x−π)/(cos x)))=lim_(x→(π/2)) (((2xsin x−π)/(sin ((π/2)−x)))) let (π/2)−x= t ,t→0 lim_(t→0) ((2((π/2)−t)sin ((π/2)−t)−π)/(sin t)) =lim_(t→0) (((π−2t)cos t−π)/(sin t)) =lim_(t→0) ((π(cos t−1)−2t cos t)/(sin t)) =lim_(t→0) ((−2π sin^2 (1/2)t−2t cos t)/(sin t)) =−2

$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\left(\frac{\mathrm{2xsin}\:\mathrm{x}−\pi}{\mathrm{cos}\:\mathrm{x}}\right)=\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\frac{\mathrm{2xsin}\:\mathrm{x}−\pi}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}\right) \\ $$$$\mathrm{let}\:\frac{\pi}{\mathrm{2}}−\mathrm{x}=\:\mathrm{t}\:,\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−\mathrm{t}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{t}\right)−\pi}{\mathrm{sin}\:\mathrm{t}}\: \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\pi−\mathrm{2t}\right)\mathrm{cos}\:\mathrm{t}−\pi}{\mathrm{sin}\:\mathrm{t}} \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\pi\left(\mathrm{cos}\:\mathrm{t}−\mathrm{1}\right)−\mathrm{2t}\:\mathrm{cos}\:\mathrm{t}}{\mathrm{sin}\:\mathrm{t}} \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}\pi\:\mathrm{sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}−\mathrm{2t}\:\mathrm{cos}\:\mathrm{t}}{\mathrm{sin}\:\mathrm{t}} \\ $$$$=−\mathrm{2}\: \\ $$

Commented by saly last updated on 13/Aug/21

than you very much !

$$\:\:{than}\:{you}\:{very}\:{much}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com