Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 15052 by Tinkutara last updated on 07/Jun/17

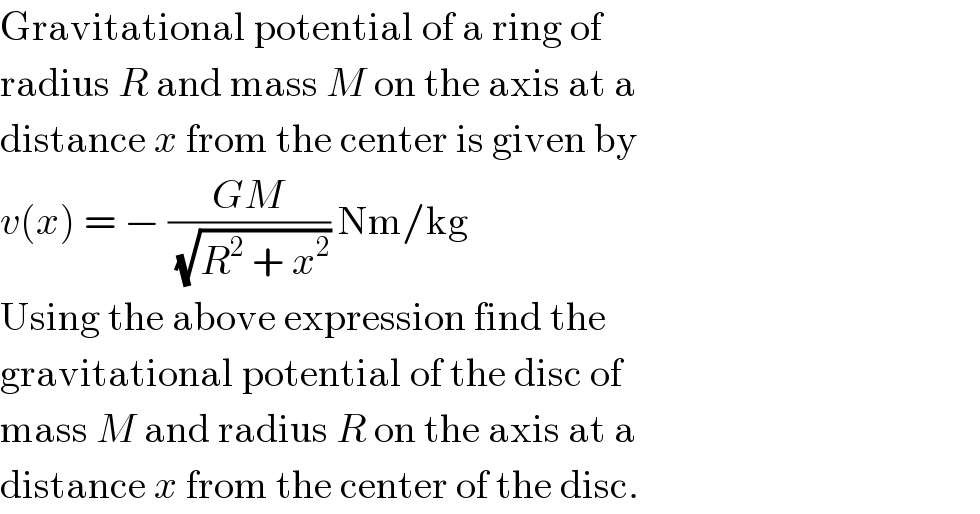
Gravitational potential of a ring of radius R and mass M on the axis at a distance x from the center is given by v(x) = − ((GM)/(√(R^2 + x^2 ))) Nm/kg Using the above expression find the gravitational potential of the disc of mass M and radius R on the axis at a distance x from the center of the disc.

$$\mathrm{Gravitational}\:\mathrm{potential}\:\mathrm{of}\:\mathrm{a}\:\mathrm{ring}\:\mathrm{of} \\ $$$$\mathrm{radius}\:{R}\:\mathrm{and}\:\mathrm{mass}\:{M}\:\mathrm{on}\:\mathrm{the}\:\mathrm{axis}\:\mathrm{at}\:\mathrm{a} \\ $$$$\mathrm{distance}\:{x}\:\mathrm{from}\:\mathrm{the}\:\mathrm{center}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by} \\ $$$${v}\left({x}\right)\:=\:−\:\frac{{GM}}{\sqrt{{R}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} }}\:\mathrm{Nm}/\mathrm{kg} \\ $$$$\mathrm{Using}\:\mathrm{the}\:\mathrm{above}\:\mathrm{expression}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{gravitational}\:\mathrm{potential}\:\mathrm{of}\:\mathrm{the}\:\mathrm{disc}\:\mathrm{of} \\ $$$$\mathrm{mass}\:{M}\:\mathrm{and}\:\mathrm{radius}\:{R}\:\mathrm{on}\:\mathrm{the}\:\mathrm{axis}\:\mathrm{at}\:\mathrm{a} \\ $$$$\mathrm{distance}\:{x}\:\mathrm{from}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{disc}. \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Commented by Tinkutara last updated on 07/Jun/17

But answer is ((−2M)/R^2 )[(√(R^2 + x^2 )) − x]

$$\mathrm{But}\:\mathrm{answer}\:\mathrm{is}\:\frac{−\mathrm{2}{M}}{{R}^{\mathrm{2}} }\left[\sqrt{{R}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} }\:−\:{x}\right] \\ $$

Commented by mrW1 last updated on 07/Jun/17

((−2GM)/R^2 )[(√(R^2 + x^2 )) − x] =((−2GM)/R^2 )[(√(R^2 + x^2 )) − x]×(([(√(R^2 +x^2 ))+x])/((√(R^2 +x^2 ))+x)) =((−2GM)/R^2 )[R^2 + x^2 − x^2 ]×(1/((√(R^2 +x^2 ))+x)) =−((2GM)/((√(R^2 +x^2 ))+x))

$$\frac{−\mathrm{2G}{M}}{{R}^{\mathrm{2}} }\left[\sqrt{{R}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} }\:−\:{x}\right] \\ $$$$\:=\frac{−\mathrm{2G}{M}}{{R}^{\mathrm{2}} }\left[\sqrt{{R}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} }\:−\:{x}\right]×\frac{\left[\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\mathrm{x}\right]}{\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\mathrm{x}} \\ $$$$\:=\frac{−\mathrm{2G}{M}}{{R}^{\mathrm{2}} }\left[{R}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} \right]×\frac{\mathrm{1}}{\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\mathrm{x}} \\ $$$$\:=−\frac{\mathrm{2GM}}{\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\mathrm{x}} \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by ajfour last updated on 07/Jun/17

dv=−((GdM)/(√(r^2 +x^2 )))=−((G(σ)(2πrdr))/(√(r^2 +x^2 ))) v =−πσG∫_0 ^( R) (((2rdr)/(√(r^2 +x^2 )))) =−πσG[2(√(r^2 +x^2 )) ]_(r=0) ^(r=R) =−2πσG((√(R^2 +x^2 ))−R) =−2πG((M/(πR^2 )))((√(R^2 +x^2 ))−R) v(x)_(disc) =−((2GM)/R^2 )((√(R^2 −x^2 ))−R) .

$$ \\ $$$${dv}=−\frac{{GdM}}{\sqrt{{r}^{\mathrm{2}} +{x}^{\mathrm{2}} }}=−\frac{{G}\left(\sigma\right)\left(\mathrm{2}\pi{rdr}\right)}{\sqrt{{r}^{\mathrm{2}} +{x}^{\mathrm{2}} }} \\ $$$$\:\:\:{v}\:=−\pi\sigma{G}\int_{\mathrm{0}} ^{\:\:{R}} \left(\frac{\mathrm{2}{rdr}}{\sqrt{{r}^{\mathrm{2}} +{x}^{\mathrm{2}} }}\right) \\ $$$$\:\:\:\:\:\:=−\pi\sigma{G}\left[\mathrm{2}\sqrt{{r}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:\right]_{{r}=\mathrm{0}} ^{{r}={R}} \\ $$$$\:\:\:\:\:\:=−\mathrm{2}\pi\sigma{G}\left(\sqrt{{R}^{\mathrm{2}} +{x}^{\mathrm{2}} }−{R}\right)\: \\ $$$$\:\:\:\:\:\:=−\mathrm{2}\pi{G}\left(\frac{{M}}{\pi{R}^{\mathrm{2}} }\right)\left(\sqrt{{R}^{\mathrm{2}} +{x}^{\mathrm{2}} }−{R}\right) \\ $$$$\:\:\:{v}\left({x}\right)_{{disc}} \:=−\frac{\mathrm{2}{GM}}{{R}^{\mathrm{2}} }\left(\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }−{R}\right)\:. \\ $$

Commented by Tinkutara last updated on 07/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by mrW1 last updated on 07/Jun/17

m=(M/(πR^2 )) [kg/m^2 ] v_d (x)=−G∫_0 ^R ((m2πrdr)/(√(r^2 +x^2 )))=−((GM)/R^2 )∫_0 ^R ((2rdr)/(√(r^2 +x^2 ))) =−((GM)/R^2 )∫_0 ^R (dr^2 /(√(r^2 +x^2 ))) =−((2GM)/R^2 )[(√(r^2 +x^2 ))]_0 ^R =−((2GM)/R^2 )[(√(R^2 +x^2 ))−x] =−((2GM)/R^2 )[(√(R^2 +x^2 ))−x]×(([(√(R^2 +x^2 ))+x])/([(√(R^2 +x^2 ))+x])) =−((2GM)/(x+(√(R^2 +x^2 ))))

$$\mathrm{m}=\frac{\mathrm{M}}{\pi\mathrm{R}^{\mathrm{2}} }\:\left[\mathrm{kg}/\mathrm{m}^{\mathrm{2}} \right] \\ $$$$\mathrm{v}_{\mathrm{d}} \left(\mathrm{x}\right)=−\mathrm{G}\int_{\mathrm{0}} ^{\mathrm{R}} \:\frac{\mathrm{m2}\pi\mathrm{rdr}}{\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }}=−\frac{\mathrm{GM}}{\mathrm{R}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{R}} \frac{\mathrm{2rdr}}{\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }} \\ $$$$=−\frac{\mathrm{GM}}{\mathrm{R}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{R}} \frac{\mathrm{dr}^{\mathrm{2}} }{\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }} \\ $$$$=−\frac{\mathrm{2GM}}{\mathrm{R}^{\mathrm{2}} }\left[\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{R}} \\ $$$$=−\frac{\mathrm{2GM}}{\mathrm{R}^{\mathrm{2}} }\left[\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }−\mathrm{x}\right] \\ $$$$=−\frac{\mathrm{2GM}}{\mathrm{R}^{\mathrm{2}} }\left[\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }−\mathrm{x}\right]×\frac{\left[\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\mathrm{x}\right]}{\left[\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\mathrm{x}\right]} \\ $$$$=−\frac{\mathrm{2GM}}{\mathrm{x}+\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }} \\ $$

Commented by mrW1 last updated on 07/Jun/17

I write the formula in this form to make its physical meaning more clear: the distance to the center of disc is x, the distance to the edge of disc is (√(R^2 +x^2 )) the average distance to disc is d_m =((x+(√(R^2 +x^2 )))/2) v_d (x)=−((GM)/d_m )=−((2GM)/(x+(√(R^2 +x^2 ))))

$$\mathrm{I}\:\mathrm{write}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{in}\:\mathrm{this}\:\mathrm{form}\:\mathrm{to} \\ $$$$\mathrm{make}\:\mathrm{its}\:\mathrm{physical}\:\mathrm{meaning}\:\mathrm{more}\:\mathrm{clear}: \\ $$$$\mathrm{the}\:\mathrm{distance}\:\mathrm{to}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of} \\ $$$$\mathrm{disc}\:\mathrm{is}\:\mathrm{x},\:\mathrm{the}\:\mathrm{distance}\:\mathrm{to}\:\mathrm{the}\:\mathrm{edge}\:\mathrm{of} \\ $$$$\mathrm{disc}\:\mathrm{is}\:\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{average}\:\mathrm{distance}\:\mathrm{to}\:\mathrm{disc}\:\mathrm{is}\: \\ $$$$\mathrm{d}_{\mathrm{m}} =\frac{\mathrm{x}+\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{v}_{\mathrm{d}} \left(\mathrm{x}\right)=−\frac{\mathrm{GM}}{\mathrm{d}_{\mathrm{m}} }=−\frac{\mathrm{2GM}}{\mathrm{x}+\sqrt{\mathrm{R}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com