Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 150719 by mathdanisur last updated on 14/Aug/21

Commented by MJS_new last updated on 15/Aug/21

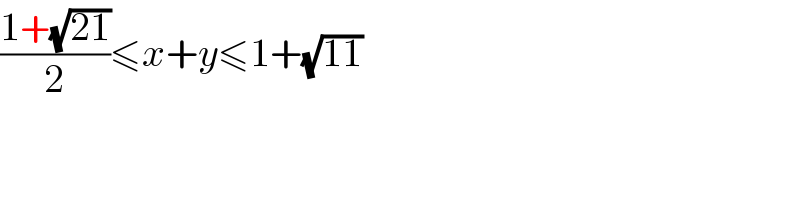
((1+(√(21)))/2)≤x+y≤1+(√(11))

$$\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}}\leqslant{x}+{y}\leqslant\mathrm{1}+\sqrt{\mathrm{11}} \\ $$

Commented by mathdanisur last updated on 15/Aug/21

ThankYou Ser, please the cases must be analyzd in detail

$$\mathrm{ThankYou}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{please}\:\mathrm{the}\:\mathrm{cases}\:\mathrm{must} \\ $$$$\mathrm{be}\:\mathrm{analyzd}\:\mathrm{in}\:\mathrm{detail} \\ $$

Commented by mathdanisur last updated on 15/Aug/21

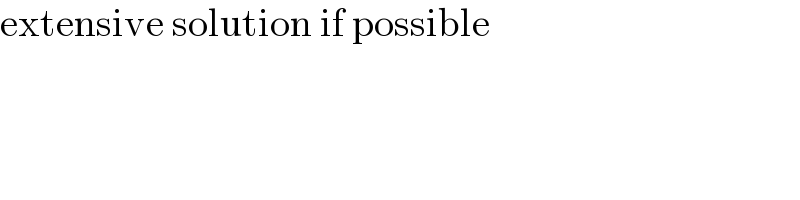
extensive solution if possible

$$\mathrm{extensive}\:\mathrm{solution}\:\mathrm{if}\:\mathrm{possible} \\ $$

Commented by mr W last updated on 15/Aug/21

typo? ((1+(√(21)))/2)≤x+y≤1+(√(11))

$${typo}? \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}}\leqslant{x}+{y}\leqslant\mathrm{1}+\sqrt{\mathrm{11}} \\ $$

Commented by MJS_new last updated on 15/Aug/21

yes, thank you

$$\mathrm{yes},\:\mathrm{thank}\:\mathrm{you} \\ $$

Answered by mr W last updated on 15/Aug/21

with condition x,y≥0, at x=0: −(√2)=(√(y+3))−y y−(√2)=(√(y+3)) y^2 −(2(√2)+1)y−1=0 y=((2(√2)+1+(√(14+4(√2))))/2) at y=0: x−(√(x+2))=(√3) (√(x+2))=x−(√3) x^2 −(2(√3)+1)x+1=0 x=((2(√3)+1+(√(9+4(√3))))/2) (x+y)_(min) =max(((2(√2)+1+(√(14+4(√2))))/2),((2(√3)+1+(√(9+4(√3))))/2)) (x+y)_(min) =((2(√3)+1+(√(9+4(√3))))/2)≈4.227 1−(1/(2(√(x+2))))=(1/(2(√(y+3))))y′−y′ for y′=−1: 1−(1/(2(√(x+2))))=−(1/(2(√(y+3))))+1 (1/( (√(x+2))))=(1/( (√(y+3)))) x+2=y+3 y=x−1 x−(√(x+2))=(√(x+2))−x+1 2x−1=2(√(x+2)) 4x^2 −8x−7=0 x=1+((√(11))/2) y=((√(11))/2) ⇒(x+y)_(max) =1+(√(11))≈4.316 without condition x,y≥0, at x=−2: −2=(√(y+3))−y y−2=(√(y+3)) y^2 −5y+1=0 y=((5+(√(21)))/2) x+y=−2+((5+(√(21)))/2)=((1+(√(21)))/2) at y=−3: x−(√(x+2))=3 x−3=(√(x+2)) x^2 −7x+7=0 x=((7+(√(21)))/2) x+y=((7+(√(21)))/2)−3=((1+(√(21)))/2) (x+y)_(min) =((1+(√(21)))/2)≈2.791

$$\boldsymbol{{with}}\:\boldsymbol{{condition}}\:\:\boldsymbol{{x}},\boldsymbol{{y}}\geqslant\mathrm{0},\: \\ $$$${at}\:{x}=\mathrm{0}: \\ $$$$−\sqrt{\mathrm{2}}=\sqrt{{y}+\mathrm{3}}−{y} \\ $$$${y}−\sqrt{\mathrm{2}}=\sqrt{{y}+\mathrm{3}} \\ $$$${y}^{\mathrm{2}} −\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}\right){y}−\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}+\sqrt{\mathrm{14}+\mathrm{4}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$${at}\:{y}=\mathrm{0}: \\ $$$${x}−\sqrt{{x}+\mathrm{2}}=\sqrt{\mathrm{3}} \\ $$$$\sqrt{{x}+\mathrm{2}}={x}−\sqrt{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} −\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}+\sqrt{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$\left({x}+{y}\right)_{{min}} ={max}\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}+\sqrt{\mathrm{14}+\mathrm{4}\sqrt{\mathrm{2}}}}{\mathrm{2}},\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}+\sqrt{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}}}{\mathrm{2}}\right) \\ $$$$\left({x}+{y}\right)_{{min}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}+\sqrt{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}}}{\mathrm{2}}\approx\mathrm{4}.\mathrm{227} \\ $$$$ \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{y}+\mathrm{3}}}{y}'−{y}' \\ $$$${for}\:{y}'=−\mathrm{1}: \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{2}}}=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{y}+\mathrm{3}}}+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}+\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{{y}+\mathrm{3}}} \\ $$$${x}+\mathrm{2}={y}+\mathrm{3} \\ $$$${y}={x}−\mathrm{1} \\ $$$${x}−\sqrt{{x}+\mathrm{2}}=\sqrt{{x}+\mathrm{2}}−{x}+\mathrm{1} \\ $$$$\mathrm{2}{x}−\mathrm{1}=\mathrm{2}\sqrt{{x}+\mathrm{2}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{7}=\mathrm{0} \\ $$$${x}=\mathrm{1}+\frac{\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$${y}=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$$\Rightarrow\left({x}+{y}\right)_{{max}} =\mathrm{1}+\sqrt{\mathrm{11}}\approx\mathrm{4}.\mathrm{316} \\ $$$$ \\ $$$$\boldsymbol{{without}}\:\boldsymbol{{condition}}\:\boldsymbol{{x}},\boldsymbol{{y}}\geqslant\mathrm{0}, \\ $$$${at}\:{x}=−\mathrm{2}: \\ $$$$−\mathrm{2}=\sqrt{{y}+\mathrm{3}}−{y} \\ $$$${y}−\mathrm{2}=\sqrt{{y}+\mathrm{3}} \\ $$$${y}^{\mathrm{2}} −\mathrm{5}{y}+\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${x}+{y}=−\mathrm{2}+\frac{\mathrm{5}+\sqrt{\mathrm{21}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${at}\:{y}=−\mathrm{3}: \\ $$$${x}−\sqrt{{x}+\mathrm{2}}=\mathrm{3} \\ $$$${x}−\mathrm{3}=\sqrt{{x}+\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{7}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{7}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${x}+{y}=\frac{\mathrm{7}+\sqrt{\mathrm{21}}}{\mathrm{2}}−\mathrm{3}=\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\left({x}+{y}\right)_{{min}} =\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}}\approx\mathrm{2}.\mathrm{791} \\ $$

Commented by mathdanisur last updated on 15/Aug/21

Thank you Ser nice

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser}\:\mathrm{nice} \\ $$

Answered by MJS_new last updated on 15/Aug/21

x−(√(x+2))=(√(y+3))−y let y=m−x x−(√(x+2))=(√(m−x+3))−(m−x) m=(√(x+2))+(√(m+3−x)) ⇒ m>0 squaring and transforming m^2 −m−5=2(√(x+2))(√(m+3−x)) ⇒ m^2 +m−5≥0 ⇒ m≥((1+(√(21)))/2) ⇒ min (x+y) =((1+(√(21)))/2) squaring and transforming x^2 −(m+1)x+((m^4 −2m^3 −9m^2 +2m+1)/2)=0 D=(p^2 /4)−q=(((m+1)^2 )/4)−((m^4 −2m^3 −9m^2 +2m+1)/2)= =((m^2 (−m^2 +2m+10))/4)≥0 ⇒ m^2 −3m−10≤0∧m≥((1+(√(21)))/2) ⇒ m≤1+(√(11)) ⇒ max (x+y) =1+(√(11))

$${x}−\sqrt{{x}+\mathrm{2}}=\sqrt{{y}+\mathrm{3}}−{y} \\ $$$$\mathrm{let}\:{y}={m}−{x} \\ $$$${x}−\sqrt{{x}+\mathrm{2}}=\sqrt{{m}−{x}+\mathrm{3}}−\left({m}−{x}\right) \\ $$$${m}=\sqrt{{x}+\mathrm{2}}+\sqrt{{m}+\mathrm{3}−{x}} \\ $$$$\:\:\:\:\:\Rightarrow\:{m}>\mathrm{0} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${m}^{\mathrm{2}} −{m}−\mathrm{5}=\mathrm{2}\sqrt{{x}+\mathrm{2}}\sqrt{{m}+\mathrm{3}−{x}} \\ $$$$\:\:\:\:\:\Rightarrow\:{m}^{\mathrm{2}} +{m}−\mathrm{5}\geqslant\mathrm{0}\:\Rightarrow\:{m}\geqslant\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{min}\:\left({x}+{y}\right)\:=\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${x}^{\mathrm{2}} −\left({m}+\mathrm{1}\right){x}+\frac{{m}^{\mathrm{4}} −\mathrm{2}{m}^{\mathrm{3}} −\mathrm{9}{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}=\frac{\left({m}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{{m}^{\mathrm{4}} −\mathrm{2}{m}^{\mathrm{3}} −\mathrm{9}{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{1}}{\mathrm{2}}= \\ $$$$=\frac{{m}^{\mathrm{2}} \left(−{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{10}\right)}{\mathrm{4}}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:{m}^{\mathrm{2}} −\mathrm{3}{m}−\mathrm{10}\leqslant\mathrm{0}\wedge{m}\geqslant\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\Rightarrow\:{m}\leqslant\mathrm{1}+\sqrt{\mathrm{11}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{max}\:\left({x}+{y}\right)\:=\mathrm{1}+\sqrt{\mathrm{11}} \\ $$

Commented by mathdanisur last updated on 15/Aug/21

Thank you Ser cool

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser}\:\mathrm{cool} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com