
Question Number 150747 by mnjuly1970 last updated on 15/Aug/21
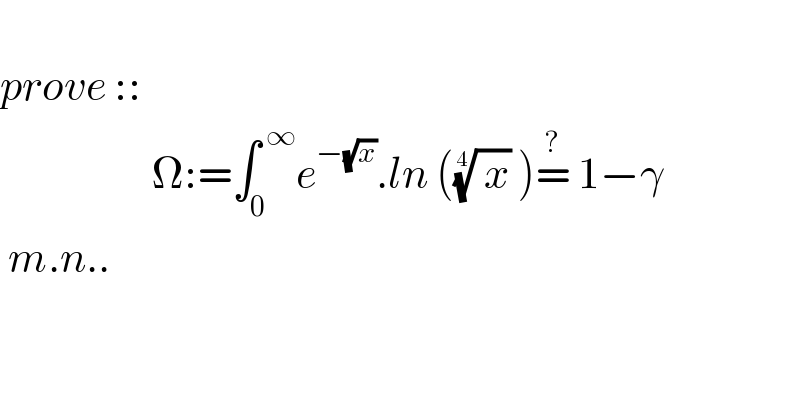
$$ \\ $$$${prove}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega:=\int_{\mathrm{0}} ^{\:\infty} {e}^{−\sqrt{{x}}} .{ln}\:\left(\sqrt[{\mathrm{4}}]{\:{x}}\:\right)\overset{?} {=}\:\mathrm{1}−\gamma \\ $$$$\:{m}.{n}.. \\ $$
Answered by Olaf_Thorendsen last updated on 15/Aug/21
![Ω = ∫_0 ^∞ e^(−(√x)) ln((x)^(1/4) ) dx Ω = ∫_0 ^∞ e^(−u) ln((√u)) (2udu) Ω = ∫_0 ^∞ ue^(−u) lnu du ψ(z) = ((∫_0 ^∞ y^(z−1) lny e^(−y) dy)/(∫_0 ^∞ y^(z−1) e^(−y) dy)) ψ(2) = ((∫_0 ^∞ y.lny e^(−y) dy)/(∫_0 ^∞ ye^(−y) dy)) = (Ω/(∫_0 ^∞ ye^(−y) dy)) ∫_0 ^∞ ue^(−u) du = [−ue^(−u) ]_0 ^∞ +∫_0 ^∞ e^(−u) du = 1 ⇒ Ω = ψ(2) ψ(z+1) = ψ(z)+(1/z) ψ(2) = ψ(1)+(1/1) = −γ+1 Ω = 1−γ = ψ(2)](Q150760.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−\sqrt{{x}}} \mathrm{ln}\left(\sqrt[{\mathrm{4}}]{{x}}\right)\:{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} \mathrm{ln}\left(\sqrt{{u}}\right)\:\left(\mathrm{2}{udu}\right) \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} \mathrm{ln}{u}\:{du} \\ $$$$\psi\left({z}\right)\:=\:\frac{\int_{\mathrm{0}} ^{\infty} {y}^{{z}−\mathrm{1}} \mathrm{ln}{y}\:{e}^{−{y}} \:{dy}}{\int_{\mathrm{0}} ^{\infty} {y}^{{z}−\mathrm{1}} {e}^{−{y}} \:{dy}} \\ $$$$\psi\left(\mathrm{2}\right)\:=\:\frac{\int_{\mathrm{0}} ^{\infty} {y}.\mathrm{ln}{y}\:{e}^{−{y}} \:{dy}}{\int_{\mathrm{0}} ^{\infty} {ye}^{−{y}} \:{dy}}\:\:=\:\frac{\Omega}{\int_{\mathrm{0}} ^{\infty} {ye}^{−{y}} \:{dy}}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} {du}\:=\:\left[−{ue}^{−{u}} \right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {du}\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\Omega\:=\:\psi\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\psi\left({z}+\mathrm{1}\right)\:=\:\psi\left({z}\right)+\frac{\mathrm{1}}{{z}} \\ $$$$\psi\left(\mathrm{2}\right)\:=\:\psi\left(\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{1}}\:=\:−\gamma+\mathrm{1} \\ $$$$ \\ $$$$\Omega\:=\:\mathrm{1}−\gamma\:=\:\psi\left(\mathrm{2}\right) \\ $$
Commented by mnjuly1970 last updated on 16/Aug/21

$${grateful}\:{mr}\:{olaf}.. \\ $$
Answered by mathmax by abdo last updated on 17/Aug/21
![Ψ=∫_0 ^∞ e^(−(√x)) ln(x^(1/4) )dx ⇒Ψ=_((√x)=t) ∫_0 ^∞ e^(−t) ln(t^(1/2) )(2t)dt =2∫_0 ^∞ (t/2)ln(t)e^(−t) dt =∫_0 ^∞ te^(−t) ln(t)dt =∫_0 ^∞ (tlnt)e^(−t) dt by parts u=tlnt and v^(′ ) =e^(−t) =[−e^(−t) (tlnt)]_0 ^∞ −∫_0 ^∞ (lnt+1)(−e^(−t) )dt =0+∫_0 ^∞ e^(−t) (1+lnt)dt =∫_0 ^∞ e^(−t) dt +∫_0 ^∞ e^(−t) lnt dt =1−γ](Q150958.png)
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\sqrt{\mathrm{x}}} \mathrm{ln}\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} \right)\mathrm{dx}\:\Rightarrow\Psi=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}\right)\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{te}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{tlnt}\right)\mathrm{e}^{−\mathrm{t}} \mathrm{dt}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}=\mathrm{tlnt}\:\mathrm{and}\:\mathrm{v}^{'\:} =\mathrm{e}^{−\mathrm{t}} \\ $$$$=\left[−\mathrm{e}^{−\mathrm{t}} \left(\mathrm{tlnt}\right)\right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \left(\mathrm{lnt}+\mathrm{1}\right)\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\mathrm{0}+\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} \left(\mathrm{1}+\mathrm{lnt}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:+\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}} \mathrm{lnt}\:\mathrm{dt} \\ $$$$=\mathrm{1}−\gamma \\ $$
