Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 151043 by mathdanisur last updated on 17/Aug/21

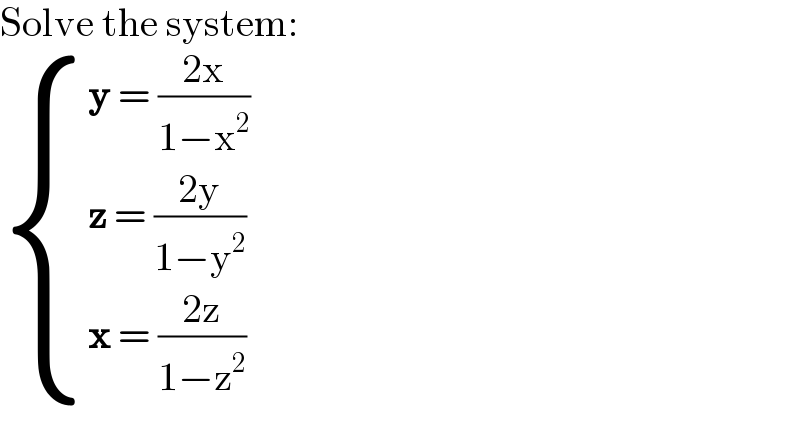
Solve the system: { ((y = ((2x)/(1−x^2 )))),((z = ((2y)/(1−y^2 )))),((x = ((2z)/(1−z^2 )))) :}

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}: \\ $$$$\begin{cases}{\boldsymbol{\mathrm{y}}\:=\:\frac{\mathrm{2x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{z}}\:=\:\frac{\mathrm{2y}}{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{x}}\:=\:\frac{\mathrm{2z}}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }}\end{cases} \\ $$

Answered by john_santu last updated on 18/Aug/21

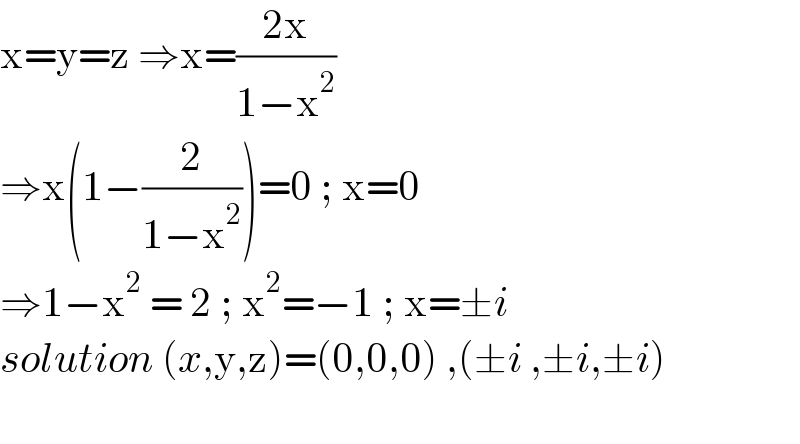
x=y=z ⇒x=((2x)/(1−x^2 )) ⇒x(1−(2/(1−x^2 )))=0 ; x=0 ⇒1−x^2 = 2 ; x^2 =−1 ; x=±i solution (x,y,z)=(0,0,0) ,(±i ,±i,±i)

$$\mathrm{x}=\mathrm{y}=\mathrm{z}\:\Rightarrow\mathrm{x}=\frac{\mathrm{2x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\: \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)=\mathrm{0}\:;\:\mathrm{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{2}\:;\:\mathrm{x}^{\mathrm{2}} =−\mathrm{1}\:;\:\mathrm{x}=\pm{i} \\ $$$${solution}\:\left({x},\mathrm{y},\mathrm{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:,\left(\pm{i}\:,\pm{i},\pm{i}\right) \\ $$$$ \\ $$

Answered by MJS_new last updated on 18/Aug/21

z=((2y)/((1−y)(1+y)))∧y=((2x)/((1−x)(1+x))) ⇒ z=((4x(1−x)(1+x))/((x^2 −2x−1)(x^2 +2x−1))) ⇒ x=((8x(1−x)(1+x)(x^2 −2x−1)(x^2 +2x−1))/(x^8 −28x^6 +70x^4 −38x^2 +1)) x^9 −20x^7 +14x^5 +28x^3 −7x=0 x_1 =0 x^8 −20x^6 +14x^4 +28x^2 −7=0 (x^2 +1)(x^6 −21x^4 +35x^2 −7)=0 x_(2, 3) =±i (x^2 )^3 −21(x^2 )^2 +35x^2 −7=0 x^2 =u+7 u^3 −112u−448=0 Trigonometric Solution u_1 =−((8(√(21)))/3)cos ((π+2arcsin ((3(√(21)))/(14)))/6) ≈−6.76808589 u_2 =−((8(√(21)))/3)sin ((arcsin ((3(√(21)))/(14)))/3) ≈−5.42758347 u_3 =((8(√(21)))/3)sin ((π+arcsin ((3(√(21)))/(14)))/3) ≈12.1956694 ⇒ x_(4, 5) ≈±.481574619 x_(6, 7) ≈±1.25396034 x_(8, 9) ≈±4.38128627 we get the following triplets ((x),(y),(x) ) (((−4.38)),((.482)),((1.25)) ) , (((−1.25)),((4.38)),((−.482)) ) , (((−.482)),((−1.25)),((4.38)) ) , ((0),(0),(0) ) , (((.482)),((1.25)),((−4.38)) ) , (((1.25)),((−4.38)),((.482)) ) , (((4.38)),((−.482)),((−1.25)) ) , (((−i)),((−i)),((−i)) ) , ((i),(i),(i) )

$${z}=\frac{\mathrm{2}{y}}{\left(\mathrm{1}−{y}\right)\left(\mathrm{1}+{y}\right)}\wedge{y}=\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)}\:\Rightarrow \\ $$$$\:\:\:\:\:{z}=\frac{\mathrm{4}{x}\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)}{\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\right)} \\ $$$$\Rightarrow \\ $$$${x}=\frac{\mathrm{8}{x}\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\right)}{{x}^{\mathrm{8}} −\mathrm{28}{x}^{\mathrm{6}} +\mathrm{70}{x}^{\mathrm{4}} −\mathrm{38}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${x}^{\mathrm{9}} −\mathrm{20}{x}^{\mathrm{7}} +\mathrm{14}{x}^{\mathrm{5}} +\mathrm{28}{x}^{\mathrm{3}} −\mathrm{7}{x}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0} \\ $$$${x}^{\mathrm{8}} −\mathrm{20}{x}^{\mathrm{6}} +\mathrm{14}{x}^{\mathrm{4}} +\mathrm{28}{x}^{\mathrm{2}} −\mathrm{7}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{6}} −\mathrm{21}{x}^{\mathrm{4}} +\mathrm{35}{x}^{\mathrm{2}} −\mathrm{7}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =\pm\mathrm{i} \\ $$$$\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{21}\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{35}{x}^{\mathrm{2}} −\mathrm{7}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} ={u}+\mathrm{7} \\ $$$${u}^{\mathrm{3}} −\mathrm{112}{u}−\mathrm{448}=\mathrm{0} \\ $$$$\mathrm{Trigonometric}\:\mathrm{Solution} \\ $$$${u}_{\mathrm{1}} =−\frac{\mathrm{8}\sqrt{\mathrm{21}}}{\mathrm{3}}\mathrm{cos}\:\frac{\pi+\mathrm{2arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}}}{\mathrm{6}}\:\approx−\mathrm{6}.\mathrm{76808589} \\ $$$${u}_{\mathrm{2}} =−\frac{\mathrm{8}\sqrt{\mathrm{21}}}{\mathrm{3}}\mathrm{sin}\:\frac{\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}}}{\mathrm{3}}\:\approx−\mathrm{5}.\mathrm{42758347} \\ $$$${u}_{\mathrm{3}} =\frac{\mathrm{8}\sqrt{\mathrm{21}}}{\mathrm{3}}\mathrm{sin}\:\frac{\pi+\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}}}{\mathrm{3}}\:\approx\mathrm{12}.\mathrm{1956694} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{4},\:\mathrm{5}} \approx\pm.\mathrm{481574619} \\ $$$${x}_{\mathrm{6},\:\mathrm{7}} \approx\pm\mathrm{1}.\mathrm{25396034} \\ $$$${x}_{\mathrm{8},\:\mathrm{9}} \approx\pm\mathrm{4}.\mathrm{38128627} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{following}\:\mathrm{triplets}\:\begin{pmatrix}{{x}}\\{{y}}\\{{x}}\end{pmatrix} \\ $$$$\begin{pmatrix}{−\mathrm{4}.\mathrm{38}}\\{.\mathrm{482}}\\{\mathrm{1}.\mathrm{25}}\end{pmatrix}\:,\:\begin{pmatrix}{−\mathrm{1}.\mathrm{25}}\\{\mathrm{4}.\mathrm{38}}\\{−.\mathrm{482}}\end{pmatrix}\:,\:\begin{pmatrix}{−.\mathrm{482}}\\{−\mathrm{1}.\mathrm{25}}\\{\mathrm{4}.\mathrm{38}}\end{pmatrix}\:,\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:,\:\begin{pmatrix}{.\mathrm{482}}\\{\mathrm{1}.\mathrm{25}}\\{−\mathrm{4}.\mathrm{38}}\end{pmatrix}\:,\:\begin{pmatrix}{\mathrm{1}.\mathrm{25}}\\{−\mathrm{4}.\mathrm{38}}\\{.\mathrm{482}}\end{pmatrix}\:,\:\begin{pmatrix}{\mathrm{4}.\mathrm{38}}\\{−.\mathrm{482}}\\{−\mathrm{1}.\mathrm{25}}\end{pmatrix}\:,\:\begin{pmatrix}{−\mathrm{i}}\\{−\mathrm{i}}\\{−\mathrm{i}}\end{pmatrix}\:,\:\begin{pmatrix}{\mathrm{i}}\\{\mathrm{i}}\\{\mathrm{i}}\end{pmatrix}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com