
Question Number 151118 by mnjuly1970 last updated on 18/Aug/21
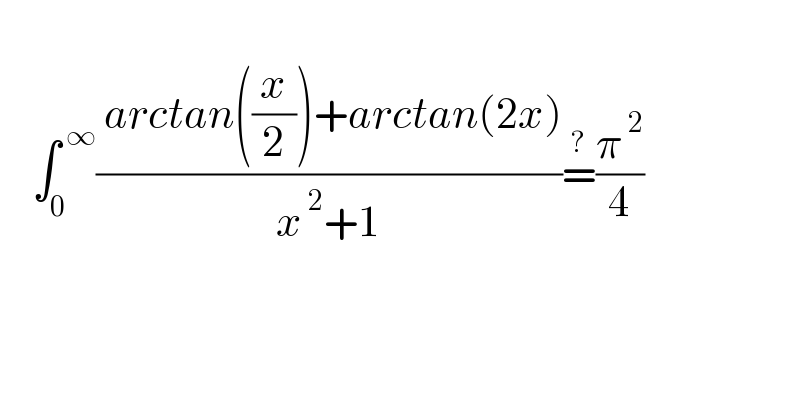
$$\:\: \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{arctan}\left(\frac{{x}}{\mathrm{2}}\right)+{arctan}\left(\mathrm{2}{x}\right)}{{x}^{\:\mathrm{2}} +\mathrm{1}}\overset{?} {=}\frac{\pi^{\:\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 18/Aug/21
![I = ∫_0 ^∞ ((arctan((x/2))+arctan(2x))/(x^2 +1)) dx Let u = (1/x) : I = ∫_0 ^∞ ((arctan((1/(2u)))+arctan((2/u)))/(u^2 +1)) du I = ∫_0 ^∞ (((π/2)−arctan(2u)+(π/2)−arctan((u/2)))/(u^2 +1)) du I = ∫_0 ^∞ (π/(u^2 +1)) du−I 2I = π[arctanu]_0 ^∞ = (π^2 /2) I = (π^2 /4)](Q151125.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{arctan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{arctan}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:\frac{\mathrm{1}}{{x}}\:: \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}{u}}\right)+\mathrm{arctan}\left(\frac{\mathrm{2}}{{u}}\right)}{{u}^{\mathrm{2}} +\mathrm{1}}\:{du} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{2}{u}\right)+\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\frac{{u}}{\mathrm{2}}\right)}{{u}^{\mathrm{2}} +\mathrm{1}}\:{du} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\pi}{{u}^{\mathrm{2}} +\mathrm{1}}\:{du}−\mathrm{I} \\ $$$$\mathrm{2I}\:=\:\pi\left[\mathrm{arctan}{u}\right]_{\mathrm{0}} ^{\infty} \:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by puissant last updated on 18/Aug/21
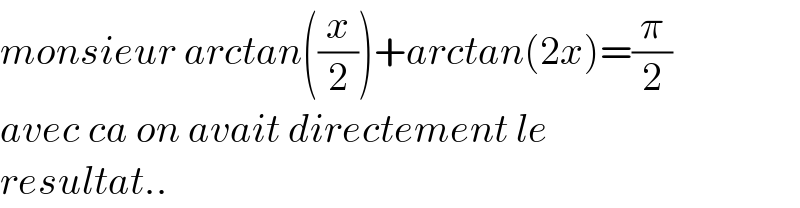
$${monsieur}\:{arctan}\left(\frac{{x}}{\mathrm{2}}\right)+{arctan}\left(\mathrm{2}{x}\right)=\frac{\pi}{\mathrm{2}} \\ $$$${avec}\:{ca}\:{on}\:{avait}\:{directement}\:{le}\: \\ $$$${resultat}.. \\ $$
Commented by Olaf_Thorendsen last updated on 18/Aug/21

$$\mathrm{Non}. \\ $$$$\mathrm{arctan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{arctan}\left(\frac{\mathrm{2}}{{x}}\right)\:=\:\frac{\pi}{\mathrm{2}}. \\ $$$$\mathrm{Deja}\:\mathrm{quand}\:{x}\:\mathrm{tend}\:\mathrm{vers}\:\mathrm{l}'\mathrm{infini} \\ $$$$\mathrm{par}\:\mathrm{exemple},\:\mathrm{vous}\:\mathrm{voyez}\:\mathrm{bien}\:\mathrm{que} \\ $$$$\mathrm{votre}\:\mathrm{formule}\:\mathrm{est}\:\mathrm{fausse}. \\ $$
Commented by mnjuly1970 last updated on 18/Aug/21
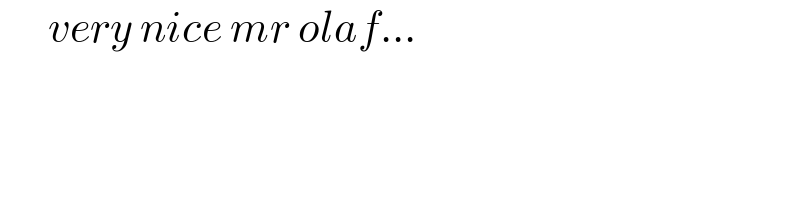
$$\:\:\:\:\:\:{very}\:{nice}\:{mr}\:{olaf}... \\ $$
Commented by puissant last updated on 18/Aug/21
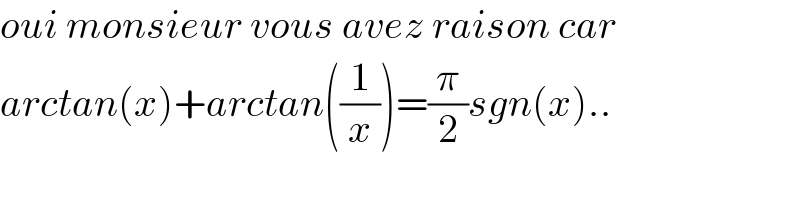
$${oui}\:{monsieur}\:{vous}\:{avez}\:{raison}\:{car} \\ $$$${arctan}\left({x}\right)+{arctan}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\pi}{\mathrm{2}}{sgn}\left({x}\right).. \\ $$
