
Question and Answers Forum
Question Number 151256 by pticantor last updated on 19/Aug/21
![A_n =2^n +3^n +4^n +5^n B_n =100^n +101^n +102^n +103^n 1)find values of n while 7∣A_n 2) show that B_n ≡A_n [7 ]](Q151256.png)
Answered by Rasheed.Sindhi last updated on 20/Aug/21

Answered by Rasheed.Sindhi last updated on 20/Aug/21
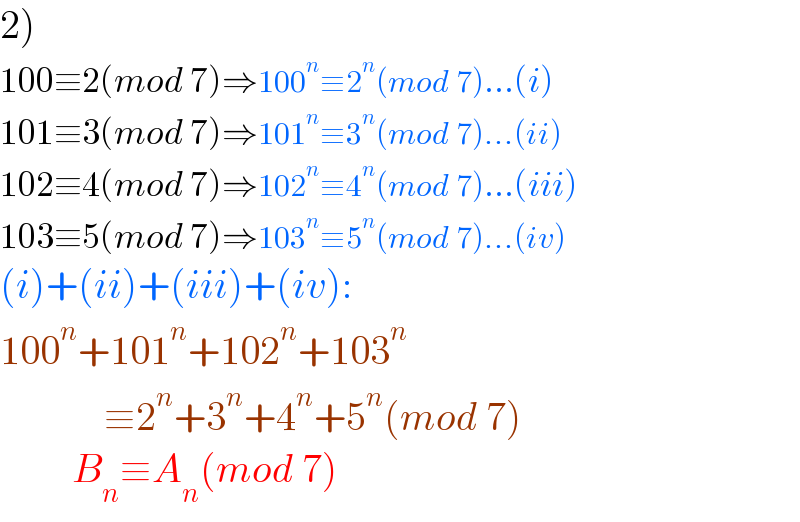
| ||
Question and Answers Forum | ||
Question Number 151256 by pticantor last updated on 19/Aug/21 | ||
![A_n =2^n +3^n +4^n +5^n B_n =100^n +101^n +102^n +103^n 1)find values of n while 7∣A_n 2) show that B_n ≡A_n [7 ]](Q151256.png) | ||
Answered by Rasheed.Sindhi last updated on 20/Aug/21 | ||
 | ||
| ||
Answered by Rasheed.Sindhi last updated on 20/Aug/21 | ||
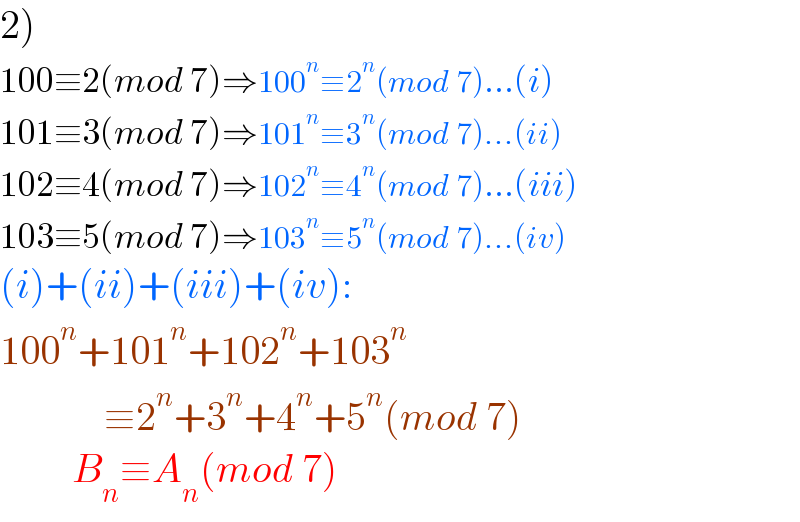 | ||
| ||