
Question and Answers Forum
Question Number 151425 by peter frank last updated on 21/Aug/21
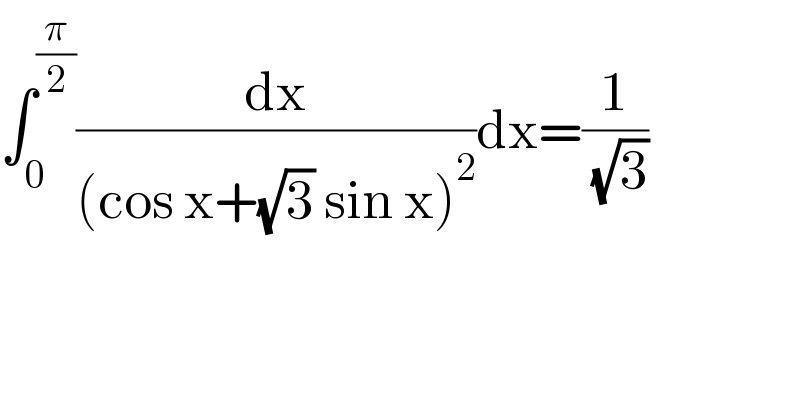
Answered by Olaf_Thorendsen last updated on 21/Aug/21
![I = ∫_0 ^(π/2) (dx/((cosx+(√3)sinx)^2 )) I = (1/4)∫_0 ^(π/2) (dx/(((1/2)cosx+((√3)/2)sinx)^2 )) I = (1/4)∫_0 ^(π/2) (dx/((cos(π/3)cosx+sin(π/3)sinx)^2 )) I = (1/4)∫_0 ^(π/2) (dx/(cos^2 (x−(π/3)))) I = (1/4)∫_(−(π/3)) ^(π/6) (du/(cos^2 u)) I = (1/4)[tanu]_(−(π/3)) ^(π/6) I = (1/4)((1/( (√3)))+(√3)) = (1/( (√3)))](Q151433.png)
Answered by MJS_new last updated on 21/Aug/21
![∫(dx/((cos x +(√3)sin x)^2 ))= [t=tan x → dx=cos^2 x dt] =∫(dt/(((√3)t+1)^2 ))=−(1/(3t+(√3)))=(1/( (√3)+3tan x))+C [(1/( (√3)+3tan x))]_0 ^(π/2) =((√3)/3)](Q151442.png)
| ||
Question and Answers Forum | ||
Question Number 151425 by peter frank last updated on 21/Aug/21 | ||
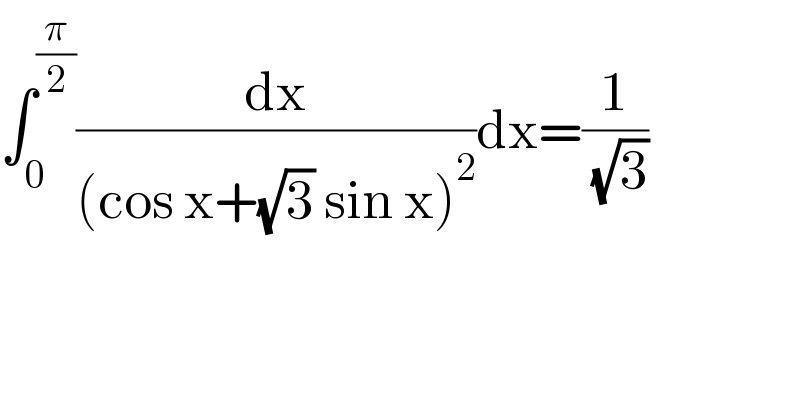 | ||
Answered by Olaf_Thorendsen last updated on 21/Aug/21 | ||
![I = ∫_0 ^(π/2) (dx/((cosx+(√3)sinx)^2 )) I = (1/4)∫_0 ^(π/2) (dx/(((1/2)cosx+((√3)/2)sinx)^2 )) I = (1/4)∫_0 ^(π/2) (dx/((cos(π/3)cosx+sin(π/3)sinx)^2 )) I = (1/4)∫_0 ^(π/2) (dx/(cos^2 (x−(π/3)))) I = (1/4)∫_(−(π/3)) ^(π/6) (du/(cos^2 u)) I = (1/4)[tanu]_(−(π/3)) ^(π/6) I = (1/4)((1/( (√3)))+(√3)) = (1/( (√3)))](Q151433.png) | ||
| ||
Answered by MJS_new last updated on 21/Aug/21 | ||
![∫(dx/((cos x +(√3)sin x)^2 ))= [t=tan x → dx=cos^2 x dt] =∫(dt/(((√3)t+1)^2 ))=−(1/(3t+(√3)))=(1/( (√3)+3tan x))+C [(1/( (√3)+3tan x))]_0 ^(π/2) =((√3)/3)](Q151442.png) | ||
| ||