
Question and Answers Forum
Question Number 151905 by mathdanisur last updated on 24/Aug/21
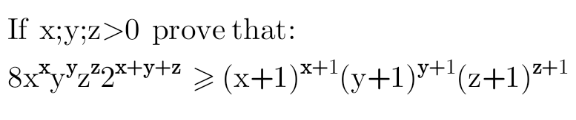
Answered by mindispower last updated on 24/Aug/21
![8x^x y^y z^z 2^(x+y+z) =2(2x)^x .2(2y)^y .(2z)^z_ 2(2t)^t ≥(t+1)^(t+1) ,t>0 ⇔2^(t+1) ≥t(1+(1/t))^(t+1) ⇔(t+1)ln(2)≥ln(t)+(t+1)ln(1+(1/t)) f(t)=(t+1)ln(2)−ln(t)−(t+1)ln(1+(1/t)) f′(t)=ln(2)−(1/t)−ln(1+(1/t))+(1/t)=ln(((2t)/(t+1))) f′(t)≥0,t∈[1,+∞[^� ,f′(t)<0,t∈]0,1[ ⇒f(t)≥f(1)=0 ⇒∀t>0,2.(2t)^(t+1) ≥(t+1)^(t+1) ⇒2.(2x)^(x+1) .2(2y)^(y+1) .2(2z)^(z+1) ≥(x+1)^(x+1) (y+1)^(y+1) (z+1)^(z+1) ⇔8x^x .y^y .z^z .2^(x+y+z) ≥(x+1)^(x+1) (y+1)^(y+1) (z+1)^(z+1)](Q151939.png)
Commented by mathdanisur last updated on 24/Aug/21

Commented by mindispower last updated on 28/Aug/21

| ||
Question and Answers Forum | ||
Question Number 151905 by mathdanisur last updated on 24/Aug/21 | ||
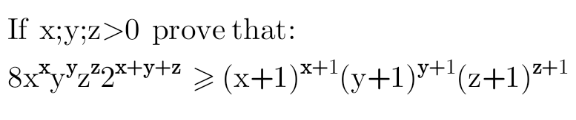 | ||
Answered by mindispower last updated on 24/Aug/21 | ||
![8x^x y^y z^z 2^(x+y+z) =2(2x)^x .2(2y)^y .(2z)^z_ 2(2t)^t ≥(t+1)^(t+1) ,t>0 ⇔2^(t+1) ≥t(1+(1/t))^(t+1) ⇔(t+1)ln(2)≥ln(t)+(t+1)ln(1+(1/t)) f(t)=(t+1)ln(2)−ln(t)−(t+1)ln(1+(1/t)) f′(t)=ln(2)−(1/t)−ln(1+(1/t))+(1/t)=ln(((2t)/(t+1))) f′(t)≥0,t∈[1,+∞[^� ,f′(t)<0,t∈]0,1[ ⇒f(t)≥f(1)=0 ⇒∀t>0,2.(2t)^(t+1) ≥(t+1)^(t+1) ⇒2.(2x)^(x+1) .2(2y)^(y+1) .2(2z)^(z+1) ≥(x+1)^(x+1) (y+1)^(y+1) (z+1)^(z+1) ⇔8x^x .y^y .z^z .2^(x+y+z) ≥(x+1)^(x+1) (y+1)^(y+1) (z+1)^(z+1)](Q151939.png) | ||
| ||
Commented by mathdanisur last updated on 24/Aug/21 | ||
 | ||
Commented by mindispower last updated on 28/Aug/21 | ||
 | ||