
Question and Answers Forum
Question Number 151979 by mathdanisur last updated on 24/Aug/21
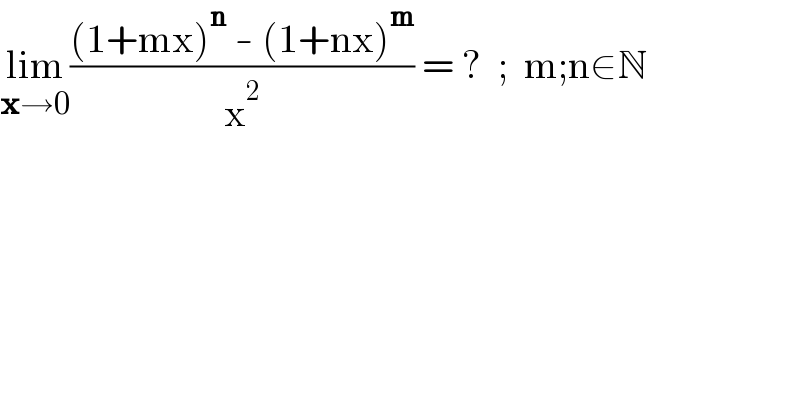
Answered by mr W last updated on 24/Aug/21
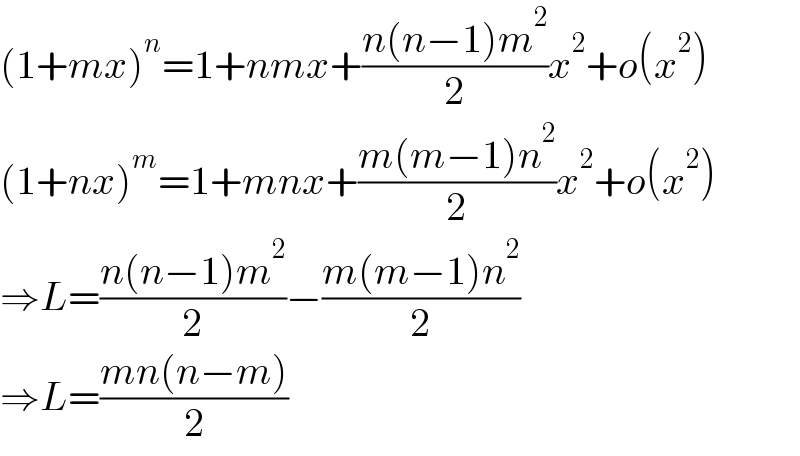
Commented by mathdanisur last updated on 24/Aug/21

Commented by mathdanisur last updated on 25/Aug/21

Answered by mr W last updated on 24/Aug/21
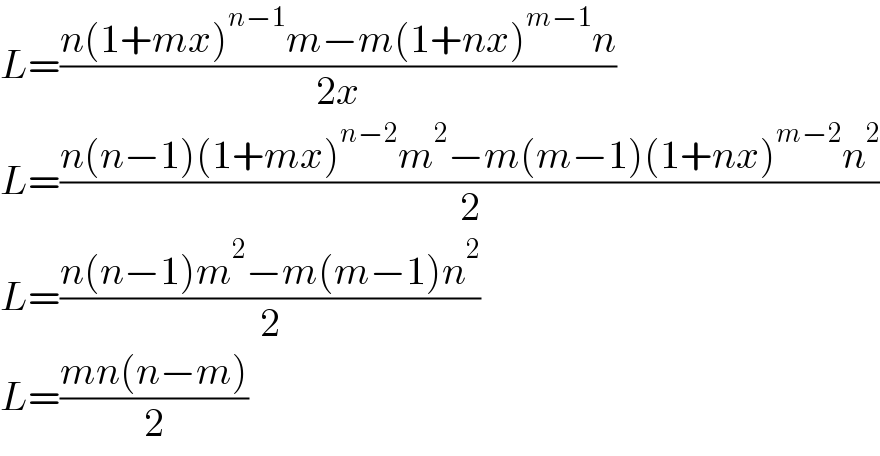
Answered by Kamel last updated on 25/Aug/21
![With classic method: L=lim_(x→0) (((1+mx)^n −(1+nx)^m )/x^2 ), m,n∈N. =lim_(x→0) ((((1+mx)^n −1)−((1+nx)^m −1))/x^2 ) =lim_(x→0) ((mx(1+(1+mx)+(1+mx)^2 +...+(1+mx)^(n−1) )−nx(1+1+nx+(1+nx)^2 +...(1+nx)^(m−1) ))/x^2 ) =lim_(x→0) ((m(1+(1+mx)+(1+mx)^2 +...+(1+mx)^(n−1) )−n(1+1+nx+(1+nx)^2 +...(1+nx)^(m−1) ))/x) =lim_(x→0) ((m(1+(1+mx)+(1+mx)^2 +...+(1+mx)^(n−1) −n)−n(1+1+nx+(1+nx)^2 +...(1+nx)^(m−1) −m))/x) =lim_(x→0) [m(((1+mx−1)/x)+(((1+mx)^2 −1)/x)+...+(((1+mx)^(n−1) −1)/x))−n(((1+nx−1)/x)+(((1+nx)^2 −1)/x)+...+(((1+nx)^(m−1) −1)/x))] lim_(x→0) (((1+ax)^p −1)/x)=((ax(1+1+ax+(1+ax)^2 +...+(1+ax)^(p−1) )/x)=ap ∴ L=m(m+2m+3m+...+(n−1)m)−n(n+2n+3n+...n(m−1)) =m^2 ((n(n−1))/2)−n^2 ((m(m−1))/2) =((mn)/2)(nm−m−nm+n)=((mn(n−m))/2) ∴ lim_(x→0) (((1+mx)^n −(1+nx)^m )/x^2 )=((mn(n−m))/2) KAMEL BENAICHA](Q152004.png)
Commented by mathdanisur last updated on 25/Aug/21

