
Question Number 152019 by mathdanisur last updated on 25/Aug/21
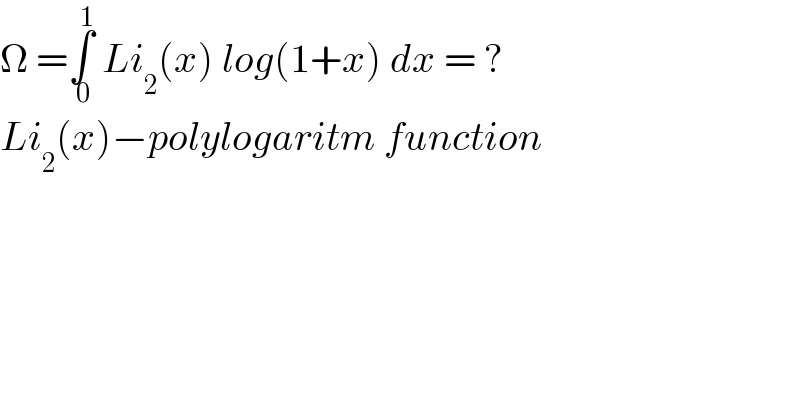
$$\Omega\:=\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:{Li}_{\mathrm{2}} \left({x}\right)\:{log}\left(\mathrm{1}+{x}\right)\:{dx}\:=\:? \\ $$$${Li}_{\mathrm{2}} \left({x}\right)−{polylogaritm}\:{function} \\ $$
Answered by mnjuly1970 last updated on 25/Aug/21

$$\: \\ $$
Answered by Olaf_Thorendsen last updated on 25/Aug/21
![Ω = ∫_0 ^1 Li_2 (x)log(1+x) dx Li_2 (x) = Σ_(k=1) ^∞ (x^k /k^2 ) ∫Li_2 (x)dx = Σ_(k=1) ^∞ (x^(k+1) /(k^2 (k+1))) Ω = [Σ_(k=1) ^∞ (x^(k+1) /(k^2 (k+1))).log(1+x)]_0 ^1 −∫_0 ^1 Σ_(k=1) ^∞ (x^(k+1) /(k^2 (k+1))).(dx/(1+x)) Ω = log2Σ_(k=1) ^∞ (1/(k^2 (k+1)))−Σ_(k=1) ^∞ (1/(k^2 (k+1)))∫_0 ^1 (x^(k+1) /(1+x)) dx ∫_0 ^1 (x^(k+1) /(1+x)) dx = −∫_0 ^1 ((1−x^(k+1) )/(1+x)) dx+∫_0 ^1 (dx/(1+x)) ∫_0 ^1 (x^(k+1) /(1+x)) dx = −∫_0 ^1 Σ_(p=0) ^k x^p dx+∫_0 ^1 (dx/(1+x)) ∫_0 ^1 (x^(k+1) /(1+x)) dx = [−Σ_(p=0) ^k (x^(p+1) /(p+1)) dx+log(1+x)]_0 ^1 ∫_0 ^1 (x^(k+1) /(1+x)) dx = −Σ_(p=0) ^k (1/(p+1)) dx+log2 = log2−H_(k+1) Ω = log2Σ_(k=1) ^∞ (1/(k^2 (k+1)))−Σ_(k=1) ^∞ ((log2−H_(k+1) )/(k^2 (k+1))) Ω = Σ_(k=1) ^∞ (H_(k+1) /(k^2 (k+1))) ...break... I come back](Q152048.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left({x}\right)\mathrm{log}\left(\mathrm{1}+{x}\right)\:{dx} \\ $$$$\mathrm{Li}_{\mathrm{2}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{k}} }{{k}^{\mathrm{2}} } \\ $$$$\int\mathrm{Li}_{\mathrm{2}} \left({x}\right){dx}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{k}+\mathrm{1}} }{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)} \\ $$$$\Omega\:=\:\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{k}+\mathrm{1}} }{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)}.\mathrm{log}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{k}+\mathrm{1}} }{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)}.\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$\Omega\:=\:\mathrm{log2}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{k}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{k}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{k}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{k}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{p}=\mathrm{0}} {\overset{{k}} {\sum}}{x}^{{p}} \:{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{k}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx}\:=\:\left[−\underset{{p}=\mathrm{0}} {\overset{{k}} {\sum}}\frac{{x}^{{p}+\mathrm{1}} }{{p}+\mathrm{1}}\:{dx}+\mathrm{log}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{k}+\mathrm{1}} }{\mathrm{1}+{x}}\:{dx}\:=\:−\underset{{p}=\mathrm{0}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{p}+\mathrm{1}}\:{dx}+\mathrm{log2}\:=\:\mathrm{log2}−{H}_{{k}+\mathrm{1}} \\ $$$$\Omega\:=\:\mathrm{log2}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{log2}−{H}_{{k}+\mathrm{1}} }{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)} \\ $$$$\Omega\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{H}_{{k}+\mathrm{1}} }{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)} \\ $$$$...{break}...\:{I}\:{come}\:{back} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 25/Aug/21
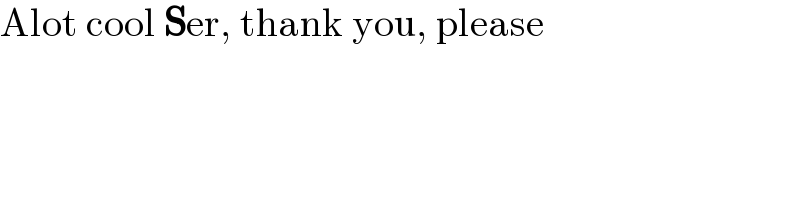
$$\mathrm{Alot}\:\mathrm{cool}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you},\:\mathrm{please} \\ $$
Commented by mathdanisur last updated on 26/Aug/21

$$\mathrm{Answer}\:\mathrm{Ser} \\ $$
Answered by Kamel last updated on 25/Aug/21

Commented by mathdanisur last updated on 26/Aug/21
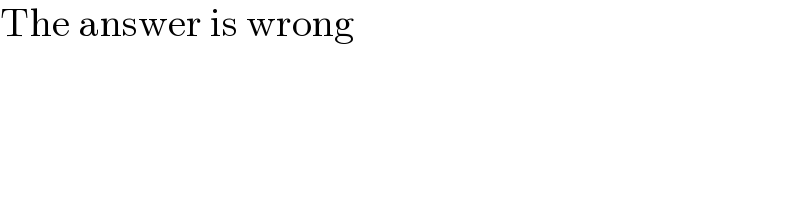
$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Answered by qaz last updated on 25/Aug/21
![Ω=[(1+x)ln(1+x)−(1+x)]Li_2 (x)∣_0 ^1 +∫_0 ^1 (1+x)[ln(1+x)−1]((ln(1−x))/x)dx =(π^2 /3)ln2−(π^2 /3)+∫_0 ^1 (((ln(1+x)ln(1−x))/x)−((ln(1−x))/x)+ln(1+x)ln(1−x)−ln(1−x))dx =(π^2 /3)ln2−(π^2 /3)−(5/8)ζ(3)+(π^2 /6)+(−(π^2 /6)+ln^2 2−2ln2+2)+1 =(π^2 /3)ln2−(π^2 /3)−(5/8)ζ(3)+ln^2 2−2ln2+3](Q152067.png)
$$\Omega=\left[\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\left(\mathrm{1}+\mathrm{x}\right)\right]\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{1}\right]\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\mathrm{ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}−\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}+\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\mathrm{ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\mathrm{ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2ln2}+\mathrm{2}\right)+\mathrm{1} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\mathrm{ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)+\mathrm{ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2ln2}+\mathrm{3} \\ $$
Commented by mathdanisur last updated on 26/Aug/21

$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{Ser} \\ $$
