Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 152111 by peter frank last updated on 25/Aug/21

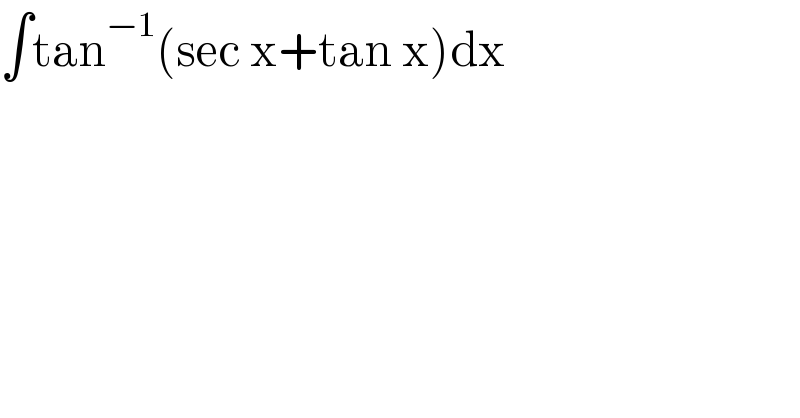
∫tan^(−1) (sec x+tan x)dx

$$\int\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$

Answered by peter frank last updated on 26/Aug/21

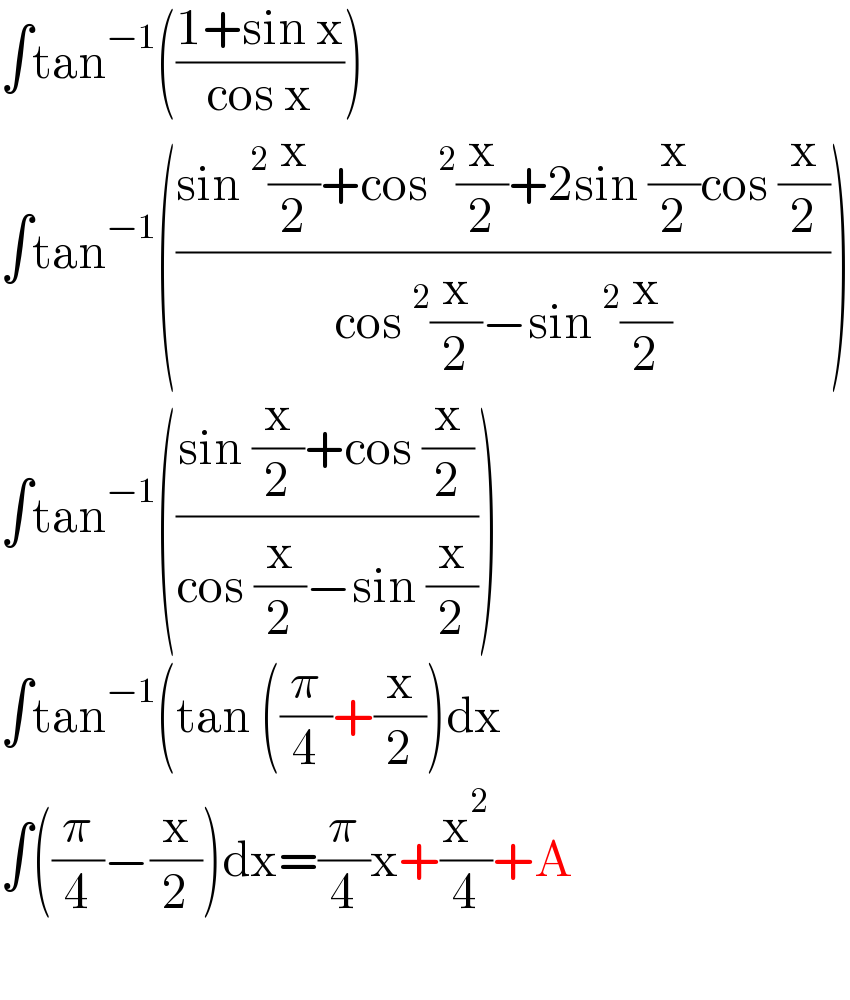
∫tan^(−1) (((1+sin x)/(cos x))) ∫tan^(−1) (((sin^2 (x/2)+cos^2 (x/2)+2sin (x/2)cos (x/2))/(cos^2 (x/2)−sin^2 (x/2)))) ∫tan^(−1) (((sin (x/2)+cos (x/2))/(cos (x/2)−sin (x/2)))) ∫tan^(−1) (tan ((π/4)+(x/2))dx ∫((π/4)−(x/2))dx=(π/4)x+(x^2 /4)+A

$$\int\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}\right) \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}+\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}\right) \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}\right) \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}\right. \\ $$$$\int\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}=\frac{\pi}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{A} \\ $$$$ \\ $$

Answered by Olaf_Thorendsen last updated on 26/Aug/21

(1/2) = ((sinx+1)/(2+2sinx)) = ((sinx+1)/(cos^2 x+sin^2 x+1+2sinx)) (1/2) = ((sinx+1)/(cos^2 x+(sinx+1)^2 )) = ((((sinx)/(cos^2 x))+(1/(cos^2 x)))/(1+((1/(cosx))+tanx)^2 )) (1/2) = (((d/dx)(secx+tanx))/(1+(secx+tanx)^2 )) F(x) = ∫arctan(secx+tanx) dx F(x) = 2×(1/2)∫arctan(secx+tanx) dx F(x) = ∫2((d(secx+tanx))/(1+(secx+ranx)^2 ))arctan(secx+tanx) dx F(x) = arctan^2 (secx+tanx)+C

$$\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{sin}{x}+\mathrm{1}}{\mathrm{2}+\mathrm{2sin}{x}}\:=\:\frac{\mathrm{sin}{x}+\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{1}+\mathrm{2sin}{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{sin}{x}+\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} {x}+\left(\mathrm{sin}{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\frac{\mathrm{sin}{x}}{\mathrm{cos}^{\mathrm{2}} {x}}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} {x}}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{cos}{x}}+\mathrm{tan}{x}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\frac{{d}}{{dx}}\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)}{\mathrm{1}+\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{arctan}\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{arctan}\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{2}\frac{{d}\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)}{\mathrm{1}+\left(\mathrm{sec}{x}+\mathrm{ran}{x}\right)^{\mathrm{2}} }\mathrm{arctan}\left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{arctan}^{\mathrm{2}} \left(\mathrm{sec}{x}+\mathrm{tan}{x}\right)+\mathrm{C} \\ $$

Commented by peter frank last updated on 26/Aug/21

first line sir.where (1/2) came from

$$\mathrm{first}\:\mathrm{line}\:\mathrm{sir}.\mathrm{where}\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{came}\:\mathrm{from} \\ $$

Commented by peter frank last updated on 26/Aug/21

it clear now.i got you

$$\mathrm{it}\:\mathrm{clear}\:\mathrm{now}.\mathrm{i}\:\mathrm{got}\:\mathrm{you} \\ $$

Answered by puissant last updated on 26/Aug/21

Q=∫arctan(secx+tanx)dx using integration by part, we have Q=xarctan(secx+tanx)−(x^2 /4)+C secx+tanx=((1+sinx)/(cosx))=tan((x/2)+(π/4)) ⇒ Q=xarctan(tan((x/2)+(π/4)))−(x^2 /4)+C ⇒ Q= ((x^2 +πx)/4)+C

$${Q}=\int{arctan}\left({secx}+{tanx}\right){dx} \\ $$$$ \\ $$$${using}\:{integration}\:{by}\:{part},\:{we}\:{have} \\ $$$${Q}={xarctan}\left({secx}+{tanx}\right)−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{C} \\ $$$${secx}+{tanx}=\frac{\mathrm{1}+{sinx}}{{cosx}}={tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\Rightarrow\:{Q}={xarctan}\left({tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right)−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{C} \\ $$$$\:\:\:\:\Rightarrow\:{Q}=\:\frac{{x}^{\mathrm{2}} +\pi{x}}{\mathrm{4}}+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com