Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 152116 by peter frank last updated on 25/Aug/21

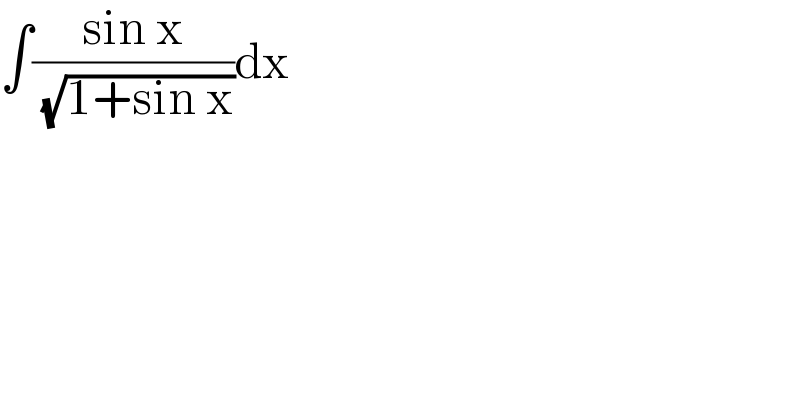
∫((sin x)/( (√(1+sin x))))dx

$$\int\frac{\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}\mathrm{dx} \\ $$

Commented by puissant last updated on 26/Aug/21

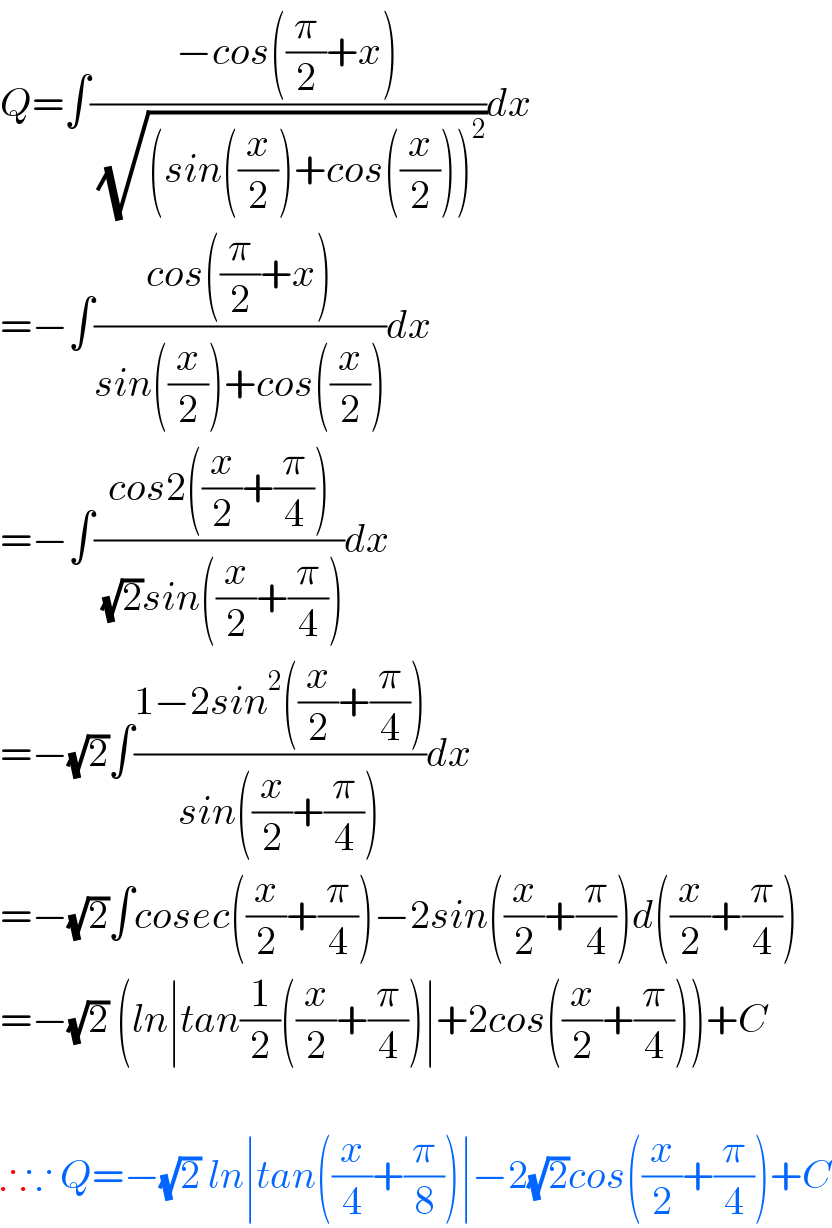
Q=∫((−cos((π/2)+x))/( (√((sin((x/2))+cos((x/2)))^2 ))))dx =−∫((cos((π/2)+x))/(sin((x/2))+cos((x/2))))dx =−∫((cos2((x/2)+(π/4)))/( (√2)sin((x/2)+(π/4))))dx =−(√2)∫((1−2sin^2 ((x/2)+(π/4)))/(sin((x/2)+(π/4))))dx =−(√2)∫cosec((x/2)+(π/4))−2sin((x/2)+(π/4))d((x/2)+(π/4)) =−(√2) (ln∣tan(1/2)((x/2)+(π/4))∣+2cos((x/2)+(π/4)))+C ∴∵ Q=−(√2) ln∣tan((x/4)+(π/8))∣−2(√2)cos((x/2)+(π/4))+C

$${Q}=\int\frac{−{cos}\left(\frac{\pi}{\mathrm{2}}+{x}\right)}{\:\sqrt{\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)+{cos}\left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }}{dx} \\ $$$$=−\int\frac{{cos}\left(\frac{\pi}{\mathrm{2}}+{x}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)+{cos}\left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$=−\int\frac{{cos}\mathrm{2}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}{sin}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)}{dx} \\ $$$$=−\sqrt{\mathrm{2}}\int\frac{\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)}{dx} \\ $$$$=−\sqrt{\mathrm{2}}\int{cosec}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right){d}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$=−\sqrt{\mathrm{2}}\:\left({ln}\mid{tan}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid+\mathrm{2}{cos}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right)+{C} \\ $$$$ \\ $$$$\therefore\because\:{Q}=−\sqrt{\mathrm{2}}\:{ln}\mid{tan}\left(\frac{{x}}{\mathrm{4}}+\frac{\pi}{\mathrm{8}}\right)\mid−\mathrm{2}\sqrt{\mathrm{2}}{cos}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)+{C} \\ $$

Commented by peter frank last updated on 26/Aug/21

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by aleks041103 last updated on 26/Aug/21

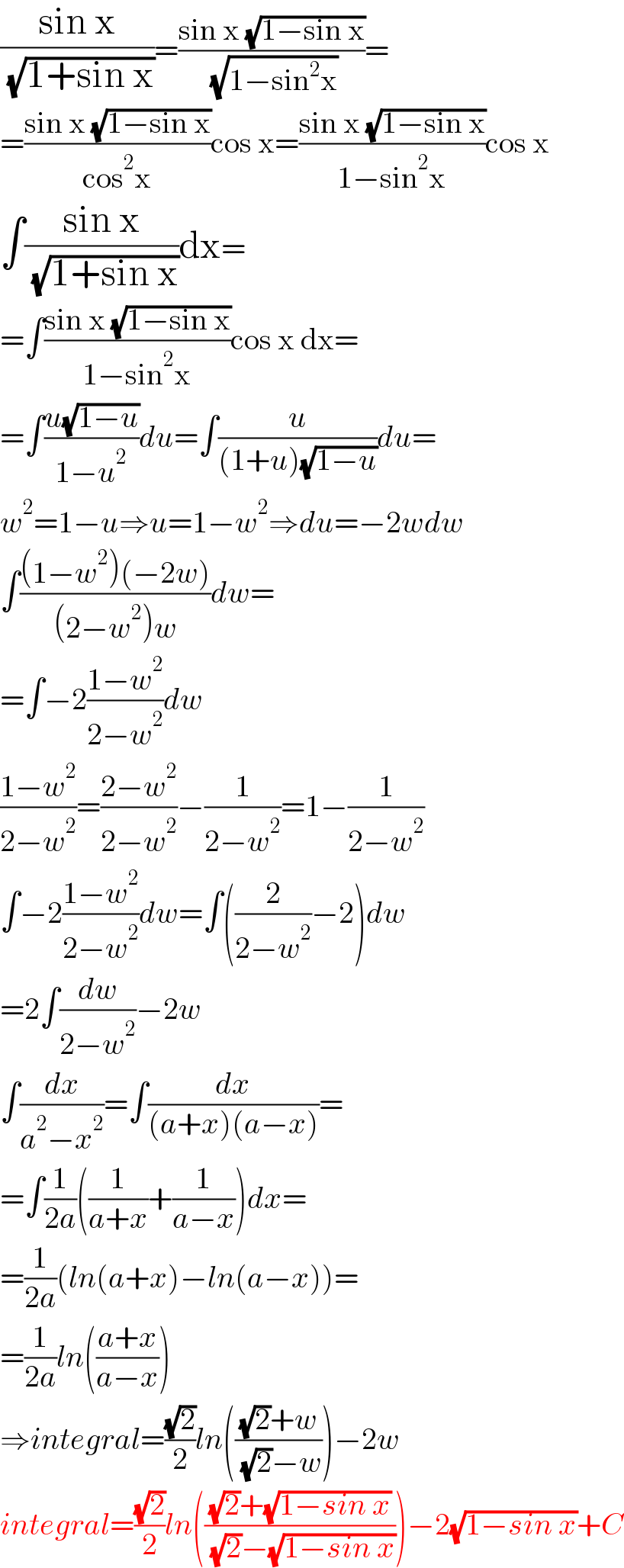
((sin x)/( (√(1+sin x))))=((sin x (√(1−sin x)))/( (√(1−sin^2 x))))= =((sin x (√(1−sin x)))/(cos^2 x))cos x=((sin x (√(1−sin x)))/(1−sin^2 x))cos x ∫((sin x)/( (√(1+sin x))))dx= =∫((sin x (√(1−sin x)))/(1−sin^2 x))cos x dx= =∫((u(√(1−u)))/(1−u^2 ))du=∫(u/((1+u)(√(1−u))))du= w^2 =1−u⇒u=1−w^2 ⇒du=−2wdw ∫(((1−w^2 )(−2w))/((2−w^2 )w))dw= =∫−2((1−w^2 )/(2−w^2 ))dw ((1−w^2 )/(2−w^2 ))=((2−w^2 )/(2−w^2 ))−(1/(2−w^2 ))=1−(1/(2−w^2 )) ∫−2((1−w^2 )/(2−w^2 ))dw=∫((2/(2−w^2 ))−2)dw =2∫(dw/(2−w^2 ))−2w ∫(dx/(a^2 −x^2 ))=∫(dx/((a+x)(a−x)))= =∫(1/(2a))((1/(a+x))+(1/(a−x)))dx= =(1/(2a))(ln(a+x)−ln(a−x))= =(1/(2a))ln(((a+x)/(a−x))) ⇒integral=((√2)/2)ln((((√2)+w)/( (√2)−w)))−2w integral=((√2)/2)ln((((√2)+(√(1−sin x)))/( (√2)−(√(1−sin x)))))−2(√(1−sin x))+C

$$\frac{\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}=\frac{\mathrm{sin}\:\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}}= \\ $$$$=\frac{\mathrm{sin}\:\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{sin}\:\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{cos}\:\mathrm{x} \\ $$$$\int\frac{\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}\mathrm{dx}= \\ $$$$=\int\frac{\mathrm{sin}\:\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}= \\ $$$$=\int\frac{{u}\sqrt{\mathrm{1}−{u}}}{\mathrm{1}−{u}^{\mathrm{2}} }{du}=\int\frac{{u}}{\left(\mathrm{1}+{u}\right)\sqrt{\mathrm{1}−{u}}}{du}= \\ $$$${w}^{\mathrm{2}} =\mathrm{1}−{u}\Rightarrow{u}=\mathrm{1}−{w}^{\mathrm{2}} \Rightarrow{du}=−\mathrm{2}{wdw} \\ $$$$\int\frac{\left(\mathrm{1}−{w}^{\mathrm{2}} \right)\left(−\mathrm{2}{w}\right)}{\left(\mathrm{2}−{w}^{\mathrm{2}} \right){w}}{dw}= \\ $$$$=\int−\mathrm{2}\frac{\mathrm{1}−{w}^{\mathrm{2}} }{\mathrm{2}−{w}^{\mathrm{2}} }{dw} \\ $$$$\frac{\mathrm{1}−{w}^{\mathrm{2}} }{\mathrm{2}−{w}^{\mathrm{2}} }=\frac{\mathrm{2}−{w}^{\mathrm{2}} }{\mathrm{2}−{w}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}−{w}^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}−{w}^{\mathrm{2}} } \\ $$$$\int−\mathrm{2}\frac{\mathrm{1}−{w}^{\mathrm{2}} }{\mathrm{2}−{w}^{\mathrm{2}} }{dw}=\int\left(\frac{\mathrm{2}}{\mathrm{2}−{w}^{\mathrm{2}} }−\mathrm{2}\right){dw} \\ $$$$=\mathrm{2}\int\frac{{dw}}{\mathrm{2}−{w}^{\mathrm{2}} }−\mathrm{2}{w} \\ $$$$\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\int\frac{{dx}}{\left({a}+{x}\right)\left({a}−{x}\right)}= \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}{a}}\left(\frac{\mathrm{1}}{{a}+{x}}+\frac{\mathrm{1}}{{a}−{x}}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}\left({ln}\left({a}+{x}\right)−{ln}\left({a}−{x}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\left(\frac{{a}+{x}}{{a}−{x}}\right) \\ $$$$\Rightarrow{integral}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}+{w}}{\:\sqrt{\mathrm{2}}−{w}}\right)−\mathrm{2}{w} \\ $$$${integral}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{1}−{sin}\:{x}}}{\:\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}−{sin}\:{x}}}\right)−\mathrm{2}\sqrt{\mathrm{1}−{sin}\:{x}}+{C} \\ $$

Commented by peter frank last updated on 26/Aug/21

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by peter frank last updated on 26/Aug/21

∫((2sin (x/2)cos (x/2))/(sin (x/(2 ))+cos (x/2))) ....

$$\int\frac{\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}\:}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$.... \\ $$

Answered by Ar Brandon last updated on 26/Aug/21

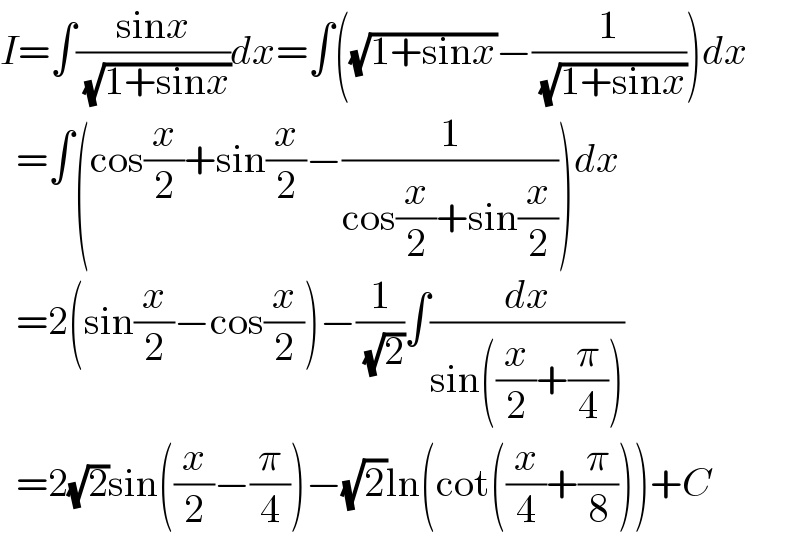
I=∫((sinx)/( (√(1+sinx))))dx=∫((√(1+sinx))−(1/( (√(1+sinx)))))dx =∫(cos(x/2)+sin(x/2)−(1/(cos(x/2)+sin(x/2))))dx =2(sin(x/2)−cos(x/2))−(1/( (√2)))∫(dx/(sin((x/2)+(π/4)))) =2(√2)sin((x/2)−(π/4))−(√2)ln(cot((x/4)+(π/8)))+C

$${I}=\int\frac{\mathrm{sin}{x}}{\:\sqrt{\mathrm{1}+\mathrm{sin}{x}}}{dx}=\int\left(\sqrt{\mathrm{1}+\mathrm{sin}{x}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{sin}{x}}}\right){dx} \\ $$$$\:\:=\int\left(\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{sin}\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{sin}\frac{{x}}{\mathrm{2}}}\right){dx} \\ $$$$\:\:=\mathrm{2}\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}−\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\:\:=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)−\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{cot}\left(\frac{{x}}{\mathrm{4}}+\frac{\pi}{\mathrm{8}}\right)\right)+{C} \\ $$

Commented by peter frank last updated on 26/Aug/21

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com