
Question and Answers Forum
Question Number 152388 by ajfour last updated on 28/Aug/21

Commented by ajfour last updated on 28/Aug/21

Commented by mr W last updated on 28/Aug/21
Commented by ajfour last updated on 28/Aug/21

Commented by ajfour last updated on 29/Aug/21
![say at vertex ball is given a max rolling speed so that it cones over without slipping. so, consider v reversed in diagram above. I=(2/5)mr^2 +mr^2 =I_0 +A (1/2)I(ω_0 ^2 −ω^2 )=mg(b^2 +rcos θ) ⇒ (7/(10))(u^2 −v^2 )=g(b^2 +rcos θ) { v^2 =u^2 −((10g)/7)(b^2 +rcos θ) } ★ differentiating wrt θ [ ((mvdv)/(rdθ))=((5mgsin θ)/7) ] ★ mgcos θ−N=((mv^2 )/r) ⇒ N=m(gcos θ−(v^2 /r)) (normal rxn goes ↓ with θ) mgsin θ−f=m((vdv)/(rdθ)) dynamic μ=(f/N) ≤μ_0 (in Q) mgsin θ−((mdv)/(rdθ))=μm(gcos θ−(v^2 /r)) μ(u,θ)=((grsin θ−((10grsin θ)/7)+u^2 )/((grcos θ−v^2 ))) μ(u,θ)=((grsin θ−((10grsin θ)/7)+u^2 )/(grcos θ−u^2 +((10g)/7)(b^2 +rcos θ))) μ(u,θ)=((7(u^2 /gr)−3sin θ)/(17cos θ+10(b^2 /r)−7(u^2 /gr))) (∂μ/∂θ)=(((−3cos θ){17cos θ+10B−7U}−{7U−3sin θ}(−17sin θ))/([17U+10B−7U]^2 )) (∂μ/∂θ)=0 ⇒ 51cos^2 θ+30Bcos θ−21Ucos θ =119Usin θ−51sin^2 θ ⇒ U(21cos θ+119sin θ)=51+30Bcos θ .......∗∗ Now μ(θ)=((7U−3sin θ)/(17cos θ+10B−7U))=μ_0 hence 7(1+μ_0 )(((51+30Bcos θ)/(21cos θ+119sin θ))) = 3sin θ+μ_0 (17cos θ+10B) from above we get θ=δ U=((51+30Bcos δ)/(21cos δ+119sin δ)) U=(u^2 /(rg)) then for θ=0° { v^2 =u^2 −((10g)/7)(b^2 +rcos θ) } ★ gives (v^2 )_Q =rg(((51+30Bcos δ)/(21cos δ+119sin δ))) −((10g)/7)(b^2 +r) _____________________](Q152550.png)
Commented by ajfour last updated on 29/Aug/21

Commented by mr W last updated on 29/Aug/21
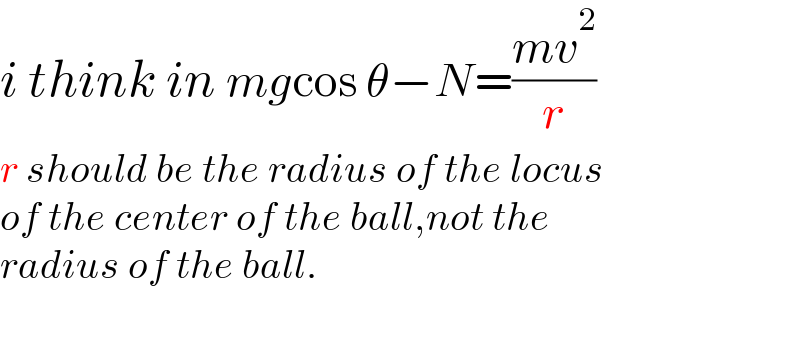
Commented by ajfour last updated on 29/Aug/21

Commented by mr W last updated on 29/Aug/21
Answered by mr W last updated on 28/Aug/21

