
Question and Answers Forum
Question Number 152496 by mathdanisur last updated on 28/Aug/21
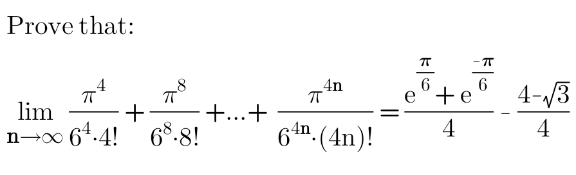
Answered by qaz last updated on 29/Aug/21
![Σ_(n=1) ^∞ (x^(4n) /((4n)!))=(x^4 /(4!))+(x^8 /(8!))+(x^(12) /(12!))+... =(1/2)[(1−(x^2 /(2!))+(x^4 /(4!))−...)+(1+(x^2 /(2!))+(x^4 /(4!))+...)]−1 =(1/2)cos x+(1/2)cosh x−1 ⇒Σ_(n=1) ^∞ (1/((4n)!))((π/6))^(4n) =(1/2)cos (π/6)+(1/2)cosh (π/6)−1=(1/4)(e^(π/6) +e^(−π/6) )−((4−(√3))/4)](Q152540.png)
Commented by mathdanisur last updated on 29/Aug/21

| ||
Question and Answers Forum | ||
Question Number 152496 by mathdanisur last updated on 28/Aug/21 | ||
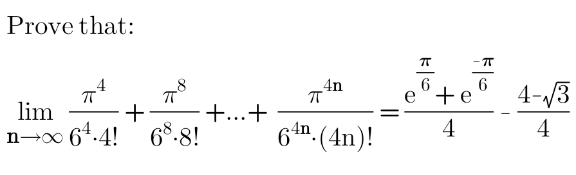 | ||
Answered by qaz last updated on 29/Aug/21 | ||
![Σ_(n=1) ^∞ (x^(4n) /((4n)!))=(x^4 /(4!))+(x^8 /(8!))+(x^(12) /(12!))+... =(1/2)[(1−(x^2 /(2!))+(x^4 /(4!))−...)+(1+(x^2 /(2!))+(x^4 /(4!))+...)]−1 =(1/2)cos x+(1/2)cosh x−1 ⇒Σ_(n=1) ^∞ (1/((4n)!))((π/6))^(4n) =(1/2)cos (π/6)+(1/2)cosh (π/6)−1=(1/4)(e^(π/6) +e^(−π/6) )−((4−(√3))/4)](Q152540.png) | ||
| ||
Commented by mathdanisur last updated on 29/Aug/21 | ||
 | ||